广东省佛山市禅城区绿岛湖学校2023-2024学年七年级下册数学4月份月考试卷

这是一份广东省佛山市禅城区绿岛湖学校2023-2024学年七年级下册数学4月份月考试卷，共13页。试卷主要包含了计算 的结果是，计算的结果是，若，，则的值为，如图，能判定的条件是，若，，则的结果是，已知，则的值是等内容，欢迎下载使用。

1．计算 的结果是
A．B．C．D．
2．计算的结果是
A．B．C．D．
3．2023年10月26日17时46分，神舟十七号载人飞船与中国空间站交会对接的过程犹如“万里穿针”，其核心部件高精度“传感器加速度计”仅为探测器升空过程中最大加速度的0.0001量级，用科学记数法表示数0.0001是
A．B．C．D．
4．过点画线段所在直线的垂线段，其中正确的是
A． B． C． D．
5．若，，则的值为
A．1B．11C．30D．35
6．如图，能判定的条件是
A．B．C． D．
7．如果多项式是一个完全平方式，则的值是
A．4B．C．8D．
8．若，，则的结果是
A．10B．18C．20D．25
9．如图，4张边长分别为、的长方形纸片围成一个正方形，从中可以得到的等式是
A．B．
C．D．
10．已知，则的值是
A．5B．9C．13D．17
二．填空题（共6小题，共18分）
11．计算： ．
12．如图，某农场在灌溉时要把水渠中的水引到点，为使渠道最短，农场工作人员过点向渠岸作垂线于点，则点即为使得所挖渠道最短的位置．其数学依据是 ．
13．已知 与是互为补角，若，则 ．
14．长方形面积是，宽为，则长方形的长是 ．
15．若（x+3）与的乘积中不含的一次项，则___________________．
16．如图，下列结论：①与是内错角；②与是同位角；③与是同旁内角；④与不是同旁内角，其中正确的是 （只填序号）．
三．解答题（共9小题,72分）
17．计算：．
计算：(-1)2018+(-12)-2-(3.14-π)0；
先化简，再求值：，其中x=2，y=-1．
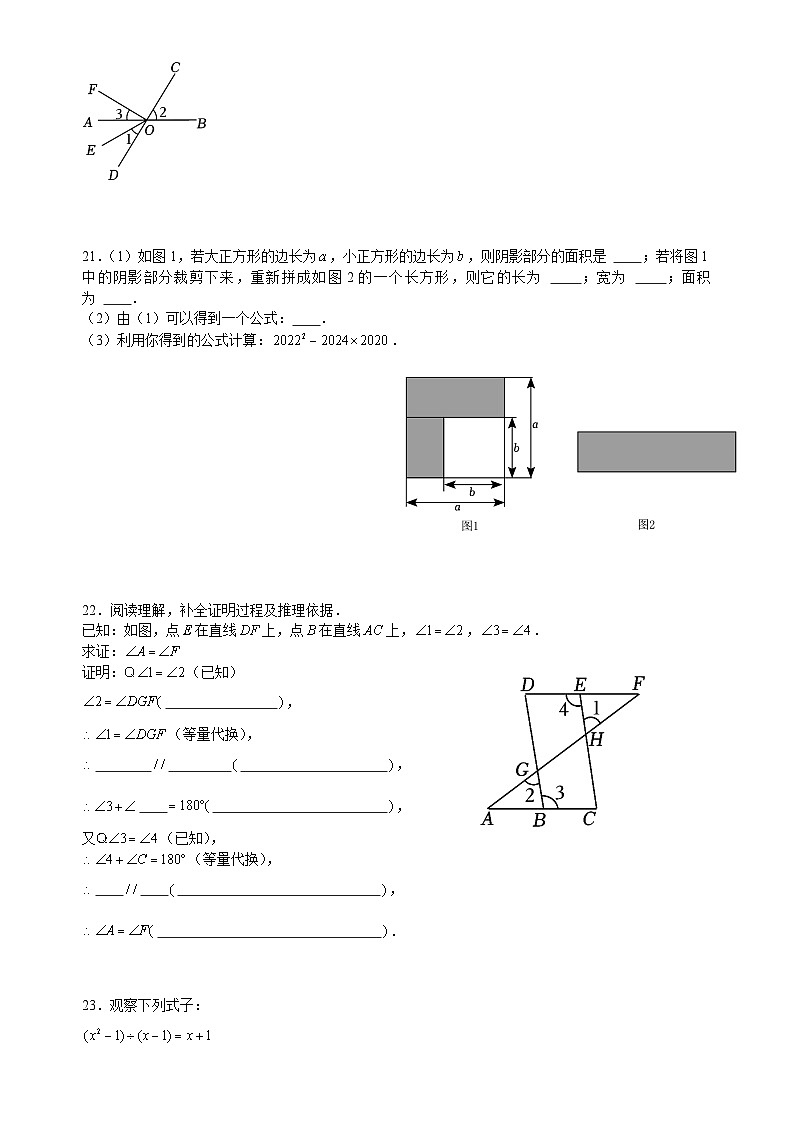
20．如图，直线，相交于点，平分，，
（1）图中的余角是 （把符合条件的角都填出来）；
（2）如果，那么根据 可得 度；
（3）如果，求和的度数．
21．（1）如图1，若大正方形的边长为，小正方形的边长为，则阴影部分的面积是 ；若将图1中的阴影部分裁剪下来，重新拼成如图2的一个长方形，则它的长为 ；宽为 ；面积为 ．
（2）由（1）可以得到一个公式： ．
（3）利用你得到的公式计算：．
22．阅读理解，补全证明过程及推理依据．
已知：如图，点在直线上，点在直线上，，．
求证：
证明：（已知）
，
（等量代换），
，
，
又（已知），
（等量代换），
，
．
23．观察下列式子：
（1）根据以上式子，请直接写出 ；
（2）根据以上式子，请直接写出的结果 为正整数）；
（3）计算：1+2+22+23+24+...+22015．
24．“以形释数”是利用数形结合思想证明代数问题的一种体现，若干张边长为的正方形纸片，边长为的正方形纸片，长和宽分别为与的长方形纸片（如图．
（1）小李同学拼成一个宽为，长为的长方形（如图，并用不同的方法计算面积，从而得出相应的等式： （答案直接填写到横线上）；
（2）如果用这三种纸片拼出一个面积为的大长方形，求需要，，三种纸片各多少张；
（3）利用上述方法，画出面积为的长方形，并求出此长方形的周长（用含，的代数式表示）．
25．如图1，是直线、内部一点，，连接，．
（1）探究猜想：
①若，，则 度；
②若，，则 度；
③猜想图1中、、的数量关系并证明你的结论．
（2）拓展应用：
如图2，射线与长方形的边交于点，与边交于点，①②③④分别是被射线隔开的4个区域（不含边界，其中区域③、④位于直线上方），是位于以上四个区域上的点，猜想：，，的关系．（直接写出结论，不要求证明）
佛山市禅城区绿岛湖学校2023-2024学年七年级下册数学第一阶段考试
一．选择题（共10小题）
1．计算 的结果是
A．B．C．D．
【解答】解：，故选：．
2．计算的结果是
A．B．C．D．
【解答】解：，故选：．
3．2023年10月26日17时46分，神舟十七号载人飞船与中国空间站交会对接的过程犹如“万里穿针”，其核心部件高精度“传感器加速度计”仅为探测器升空过程中最大加速度的0.0001量级，用科学记数法表示数0.0001是
A．B．C．D．
【解答】解：．
故选：．
4．过点画线段所在直线的垂线段，其中正确的是
A．B．C．D．
【解答】解：根据垂线段的定义，仅选项符合要求．
故选：．
5．若，，则的值为
A．1B．11C．30D．35
【解答】解：，，
，
故选：．
6．如图，能判定的条件是
A．B．C．D．
【解答】解：．当时，不能得到，故选项错误；
．当时，能得到，故选项正确；
．当时，不能得到，故选项错误；
．当时，不能得到，故选项错误；
故选：．
7．如果多项式是一个完全平方式，则的值是
A．4B．C．8D．
【解答】解：，
，
解得．
故选：．
8．若，，则的结果是
A．10B．18C．20D．25
【解答】解：当，时，
．
故选：．
9．如图，4张边长分别为、的长方形纸片围成一个正方形，从中可以得到的等式是
A．B．
C．D．
【解答】解：设大正方形的面积，小正方形的面积，
大正方形的边长为，则大正方形面积，
小正方形的边长为，则小正方形面积，
四个长方形的面积为，
，
，
故选：．
10．已知，则的值是
A．5B．9C．13D．17
【解答】解：令，则原式可化简为，则，
解得：，即．
故选：．
二．填空题（共6小题）
11．计算： ．
【解答】解：．
故答案为：．
12．如图，某农场在灌溉时要把水渠中的水引到点，为使渠道最短，农场工作人员过点向渠岸作垂线于点，则点即为使得所挖渠道最短的位置．其数学依据是 垂线段最短 ．
【解答】解：直线外一点与直线上所有的点的连线段中，垂线段最短．
故答案为：垂线段最短．
13．已知 与是互为补角，若，则 ．
故答案为：138°．
14．长方形面积是，宽为，则长方形的长是 ．
【解答】解：根据题意列得：．
故答案为：．
15．若(x+3)与的乘积中不含的一次项，则 ．
16．如图，下列结论：①与是内错角；②与是同位角；③与是同旁内角；④与不是同旁内角，其中正确的是 ①②③ （只填序号）．
【解答】解：与是直线、直线，被直线所截的一对内错角，因此①符合题意；
与是直线、直线，被直线所截的一对同位角，因此②符合题意；
与是直线、直线，被直线所截的一对同旁内角，因此③符合题意，
与是直线、直线，被直线所截的一对同旁内角，因此④不符合题意，
故答案为：①②③．
三．解答题（共9小题）
17．计算：．
【解答】解：原式
．
18．计算：(-1)2018+(-12)-2-(3.14-π)0；
【解答】解：(-1)2018+(-12)-2-(3.14-π)0；
=1+4-1
=4；
19．先化简，再求值：，其中x=2，y=-1
【解答】解：
，
当x=2，y=-1时，原式=4×2×(-1)+9=-8+9=1
20．如图，直线，相交于点，平分，，
（1）图中的余角是 、 （把符合条件的角都填出来）；
（2）如果，那么根据 可得 度；
（3）如果，求和的度数．
【解答】解：（1），
，
，，
的余角是、；
故答案为：、；
（2），
；
故答案为：对顶角相等；160；
（3）平分，
，
，．
21．（1）如图1，若大正方形的边长为，小正方形的边长为，则阴影部分的面积是 ；若将图1中的阴影部分裁剪下来，重新拼成如图2的一个长方形，则它的长为 ；宽为 ；面积为 ．
（2）由（1）可以得到一个公式： ．
（3）利用你得到的公式计算：．
【解答】解：（1）根据题意可得：
图1阴影部分的面积，
图2长方形的长为：，
图2长方形的宽为：，
面积为：，
故答案为：，，，；
（2）由（1）可得：，
故答案为：；
（3）
．
22．阅读理解，补全证明过程及推理依据．
已知：如图，点在直线上，点在直线上，，．
求证：
证明：（已知）
对顶角相等 ，
（等量代换），
，
，
又（已知），
（等量代换），
，
．
【解答】证明：（已知），
（对顶角相等），
（等量代换），
（同位角相等，两直线平行），
（两直线平行，同旁内角互补），
又（已知），
（等量代换），
（同旁内角互补，两直线平行），
（两直线平行，内错角相等）．
故答案为：对顶角相等；；；同位角相等，两直线平行；；两直线平行，同旁内角互补；；；同旁内角互补，两直线平行；两直线平行，内错角相等．
23．观察下列式子：
（1）根据以上式子，请直接写出 ；
（2）根据以上式子，请直接写出的结果 为正整数）；
（3）计算：1+2+22+23+24+...+22015
【解答】解：（1）由题意得，．
故答案为：．
（2）由题意得，．
故答案为：．
（3）由题意得，1+2+22+23+24+...+22015=(22016-1)÷(2-1)=22016-1
24．“以形释数”是利用数形结合思想证明代数问题的一种体现，若干张边长为的正方形纸片，边长为的正方形纸片，长和宽分别为与的长方形纸片（如图．
（1）小李同学拼成一个宽为，长为的长方形（如图，并用不同的方法计算面积，从而得出相应的等式： （答案直接填写到横线上）；
（2）如果用这三种纸片拼出一个面积为的大长方形，求需要，，三种纸片各多少张；
（3）利用上述方法，画出面积为的长方形，并求出此长方形的周长（用含，的代数式表示）．
【解答】解：（1）图2是长为，宽为的长方形，因此面积为，图2是6个部分的 面积和，即，
因此，
故答案为：；
（2），
纸片的面积为，纸片的面积为，纸片的面积为，
纸片需要2张，纸片需要3张，纸片需要7张；
（3）由于，
因此可以拼成长为，宽为的长方形，
如图所示：
这个长方形的周长为：，
答：此长方形的周长为．
25．如图1，是直线、内部一点，，连接，．
（1）探究猜想：
①若，，则 70 度；
②若，，则 度；
③猜想图1中、、的数量关系并证明你的结论．
（2）拓展应用：
如图2，射线与长方形的边交于点，与边交于点，①②③④分别是被射线隔开的4个区域（不含边界，其中区域③、④位于直线上方），是位于以上四个区域上的点，猜想：，，的关系．（直接写出结论，不要求证明）
【解答】解：（1）①如图①，过点作，
，
，
，，
，，
，
故答案为：70；
②过点作，
，
，
，，
，，
，
故答案为：80；
③猜想：．
理由：过点作，
（平行于同一条直线的两直线平行），
，（两直线平行，内错角相等），
（等量代换）．
（2）根据题意得：
点在区域①时，；
点在区域②时，；
点在区域④时，；
点在区域③时，．