山东省东营市广饶县乐安街道乐安中学2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版）

这是一份山东省东营市广饶县乐安街道乐安中学2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版），文件包含山东省东营市广饶县乐安街道乐安中学2023-2024学年七年级下学期3月月考数学试题原卷版docx、山东省东营市广饶县乐安街道乐安中学2023-2024学年七年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。

一、单选题（共11小题，满分33分）
1. 在下列方程组：①，②，③，④，⑤中，是二元一次方程组的是（ ）
A. ①②③B. ①②④C. ①②⑤D. ①②③⑤
【答案】C
【解析】
【分析】由二元一次方程组的概念可直接判断得到答案．
【详解】解：由二元一次方程组的概念：方程组中含有两个未知数，且含未知数的项的次数都是一次；可判断①②⑤是二元一次方程组．
故选：C．
【点睛】本题考查二元一次方程组的概念，熟练掌握相关知识是解题的关键．
2. 如图，下列四个图中，不能判断不能判定的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】结合图形分析两角的位置关系，根据平行线的判定方法分别判断即可．
【详解】解：A、∠1和∠2是同位角，∠1=∠2，∴a∥b；
B、∠1和∠2是同位角，∠1=∠2，∴a∥b；
C、∠1和∠2是同位角，但不是a，b被一条直线所截，故不能判定a∥b；
D、如图，∠1=∠3，∠1=∠2，∴∠2=∠3，∴a∥b；
故选C．
【点睛】本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．
3. 用加减消元法解方程时，下列求解过程正确的是（ ）
A. 要消去y，可以将①②B. 要消去x，可以将①②
C. 要消去y，可以将①②D. 要消去x，可以将①②
【答案】D
【解析】
【分析】根据加减消元法求解即可．
【详解】解：要消去y，可以将①②，
要消去x，可以将①②，
故选：D．
【点睛】本题考查了解二元一次方程组，熟练掌握加减消元法是解题的关键．
4. 已知是方程解，则的值为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】将代入原方程，可得出关于的一元一次方程，解之即可求出的值．
【详解】解：∵是方程的解，
∴，
解得：，
∴的值为．
故选：A．
【点睛】本题考查二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．理解二元一次方程解的定义是解题的关键．
5. 下列句子，是命题的是（ ）
A. 今天的空气好清新B. 年月日，神舟十二号发射升空
C. 作一条长为 的线段D. 同旁内角互补
【答案】D
【解析】
【分析】本题考查命题的判断，熟知命题的定义：判断一件事情的句子叫做命题，数学中的命题常可以写成：如果…，那么…，据此逐项判断即可．
【详解】解：A、今天的空气好清新，没有作出判断，不是命题，不符合题意；
B、年月日，神舟十二号发射升空，没有作出判断，不是命题，不符合题意；
C、作一条长为 线段，没有作出判断，不是命题，不符合题意；
D、同旁内角互补，作出判断，是命题，符合题意；
故选：D．
6. 下列命题中，真命题有（ ）
（1）同旁内角互补；
（2）和为0的两个数互为相反数；
（3）若|a|＝|b|，则a＝b；
（4）相等的角是对顶角．
A 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】利用平行线的性质、相反数的定义、绝对值的意义及对顶角的定义分别判断后即可确定正确的选项．
【详解】解：（1）两直线平行，同旁内角互补，故原说法是假命题；
（2）和为0的两个数互为相反数，正确，符合题意；
（3）若|a|＝|b|，则a＝±b，故原说法是假命题；
（4）相等的角不一定是对顶角，故原命题错误，不符合题意，
真命题有1个，
故选：A．
【点睛】考查了命题与定理的知识，解题的关键是了解平行线的性质、相反数的定义、绝对值的意义及对顶角的定义．
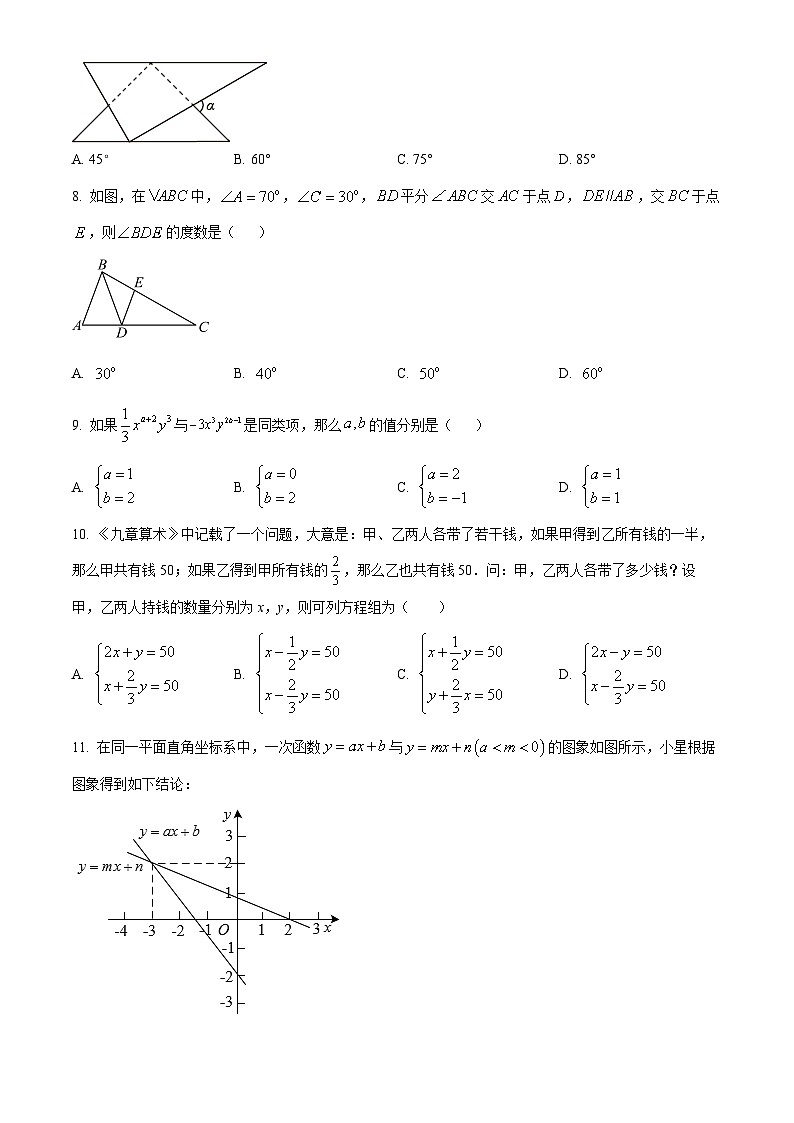
7. 一副三角板如图就置，两三角板的斜边互相平行，每个三角板的直角顶点都在另一个三角板的斜边上，图中的度数为（ ）
A. 45°B. 60°C. 75°D. 85°
【答案】C
【解析】
【分析】过顶点M作MN平行于直角三角形的斜边，则根据两直线平行内错角相等即可求得的度数．
【详解】如图，设两块三角板分别为△ABC、△DEF，DE与BC的交点为M，过点M作MN∥AB
则∠BMN=∠B=30゜
∵AB∥CD，MN∥AB
∴MN∥CD
∴∠NME=∠E=45゜
∴∠α=∠BMN+∠NME=30゜+45゜=75゜
故选：C．
【点睛】本题考查了平行线的两个性质：两直线平行内错角相等，平行于同一条直线的两条直线平行，作平行线是难点，平行线性质的应用是关键．
8. 如图，在中，，，平分交于点，，交于点，则的度数是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了平行线的性质，三角形内角和定理，角平分线定义的应用，根据三角形内角和定理求出，根据角平分线定义求出，根据平行线的性质得出即可．
【详解】解：在中，，，
，
平分，
，
，
，
故选：B．
9. 如果与是同类项，那么的值分别是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据同类项定义列出关于a、b的方程组，然后解方程组即可解答．
【详解】解：∵与是同类项，
∴，解得：，
故选：A．
【点睛】本题考查了同类项的定义、解二元一次方程组，理解同类项的定义是解答的关键．
10. 《九章算术》中记载了一个问题，大意是：甲、乙两人各带了若干钱，如果甲得到乙所有钱的一半，那么甲共有钱50；如果乙得到甲所有钱的，那么乙也共有钱50．问：甲，乙两人各带了多少钱？设甲，乙两人持钱的数量分别为x，y，则可列方程组为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据题意可得，甲的钱+乙的钱的一半=50，乙的钱+甲所有钱的=50，据此列方程组即可．
【详解】解：甲带钱x，乙带钱y，根据题意，得：
故选：C．
【点睛】本题考查了由实际问题抽象出二元一次方程组，解答此类的关键是读懂题意，设出未知数，找出合适的等量关系，列出方程组．
11. 在同一平面直角坐标系中，一次函数与的图象如图所示，小星根据图象得到如下结论：
①在一次函数的图象中，的值随着值的增大而增大；
②方程组的解为；
③方程的解为；
④当时，．
其中结论正确的个数是（ ）
A. 1B. 2C. 3D. 4
【答案】B
【解析】
【分析】由函数图象经过的象限可判断①，由两个一次函数的交点坐标可判断②，由一次函数与坐标轴的交点坐标可判断③④，从而可得答案．
【详解】解：由一次函数的图象过一，二，四象限，的值随着值的增大而减小；
故①不符合题意；
由图象可得方程组的解为，即方程组的解为；
故②符合题意；
由一次函数的图象过 则方程的解为；故③符合题意；
由一次函数的图象过 则当时，．故④不符合题意；
综上：符合题意的有②③，
故选B
【点睛】本题考查的是一次函数的性质，一次函数的图象的交点坐标与二元一次方程组的解，一次函数与坐标轴的交点问题，熟练的运用数形结合的方法解题是关键．
二、填空题（共8小题，满分32分）
12. 将命题“在同一平面内，垂直于同一条直线的两条直线平行”改写为“如果……，那么……”的形式为__________________________________________．
【答案】如果在同一平面内两条直线都垂直于同一条直线，那么这两条直线互相平行
【解析】
【分析】命题由题设和结论两部分组成，通常写成“如果…那么…”的形式．“如果”后面接题设，“那么”后面接结论．
【详解】解：命题可以改写为：如果在同一平面内两条直线垂直于同一条直线，那么这两条直线互相平行．
故答案为：如果在同一平面内两条直线垂直于同一条直线，那么这两条直线互相平行．
【点睛】本题考查命题的题设和结论，解题的关键是掌握任何一个命题都可以写成“如果…那么…”的形式．“如果”后面接题设，“那么”后面接结论．在改写过程中，不能简单地把题设部分、结论部分分别写在“如果”、“那么”后面，要适当增减词语，保证句子通顺而不改变原意．
13. 已知方程：为二元一次方程，则n的值为_______．
【答案】
【解析】
【分析】根据二元一次方程的定义解答即可．
【详解】解：因为方程为二元一次方程，
所以，
解得．
故答案为：．
【点睛】本题考查了二元一次方程的定义，二元一次方程必须符合以下三个条件：（1）方程中只含有2个未知数；（2）含未知数项的最高次数为一次；（3）方程是整式方程．
14. 已知方程组的解为则的值为______．
【答案】8
【解析】
【分析】把代入，即可求解．
【详解】解：把代入得：，
得：，
∴，
故答案为：8．
【点睛】本题考查了二元一次方程组的解，解题的关键是正确将方程组的解代入原方程组．
15. 已知方程组的解也是方程的解，则______，______．
【答案】 ①. 3 ②. 1
【解析】
【分析】联立不含a与b的方程组成方程组求出x与y的值，代入剩下的方程求出a与b的值即可．
【详解】解：联立得：，
解得：，
代入剩下的两方程得：
，
解得：，
故答案为：3，1．
【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
16. 若直线和直线的交点坐标为．则_______，_______．
【答案】 ①. 5 ②. 13
【解析】
【分析】先将点(、)代入直线中求出的值为，再将交点代入直线中即可求出的值
【详解】直线与直线交于点(、)
将点(、)代入直线中得：，
将点(、)代入直线中得：
故答案为：①；②
【点睛】本题考查了两直线相交的问题，把交点坐标代入已知直线解析式求出的值，从而确定交点的坐标是解题关键．
17. 如图，已知ABCD，∠A＝54°，∠E＝18°，则∠C的度数是_____．
【答案】36°
【解析】
【分析】设AE与CD交于点O，由ABCD，利用“两直线平行，同位角相等”可得出∠DOE的度数，再利用三角形外角的性质，即可求出∠C的度数．
【详解】解：设AE与CD交于点O，如图所示，
∵ABCD，∠A＝54°，
∴∠DOE＝∠A＝54°．
又∵∠DOE＝∠C＋∠E，∠E＝18°，
∴∠C＝∠DOE−∠E＝54°−18°＝36°．
故答案为：36°．
【点睛】本题考查了平行线的性质以及三角形外角的性质，解题的关键是：利用“两直线平行，同位角相等”找出∠DOE的度数．
18. 如图：在中，，三角形的外角和的平分线交于点，则_______．
【答案】
【解析】
【分析】根据三角形内角和定理得，由三角形的外角和的平分线交于点，可知，，再根据三角形的外角性质可得，，再将这些式子代入，进而求得，代入数据即可求出，最后根据三角形内角和定理即可求出答案．
【详解】解：，
，
三角形的外角和的平分线交于点，
，，
，，
，
，，
，
，
，
．
故答案为：．
【点睛】本题考查了三角形内角和定理，三角形外角性质，角平分线的定义，准确地运用三角形内角和定理是解题的关键．
19. 如图，是的平分线，是的平分线，与交于G，若，，则为__________．

【答案】##80度
【解析】
【分析】本题主要考查了三角形内角和的应用，首先连接，根据三角形的内角和定理，求出，∠1+∠2+∠3+∠4=70°；然后判断出，再根据是的平分线，是的平分线，判断出；最后根据三角形的内角和定理，用即可求出∠A的度数．
【详解】解：如图所示，连接，

∵，
∴，
∵，
∴，
∴，
∵是的平分线，是的平分线，
∴∠3=∠5，∠4=∠6，
又∵，
∴，
∴，
∴．
故答案为：．
三、解方程组
20. 解方程组：
（1）
（2）．
（3）；
（4）．
【答案】（1）
（2）
（3）
（4）
【解析】
【分析】本题考查解二元一次方程组，熟练掌握加减消元法和代入消元法是解答的关键．
（1）利用加减消元法解方程组即可；
（2）利用代入消元法解方程组即可；
（3）先去分母整理方程组，再利用加减消元法求解即可；
（4）先去分母整理方程组，再利用代入消元法求解即可；
【小问1详解】
解：，
得：，则，
将代入②中，得，
∴方程组的解为；
【小问2详解】
解：
由①得，
代入②中，得，则，
将代入中，得，
∴方程组的解为；
【小问3详解】
解：整理方程组，得，
得，则，
将代入②，得，
∴方程组的解为；
【小问4详解】
解：整理方程组，得，
将①代入②中，得，则，
将代入①中，得，
∴方程组的解为．
四、解答题（共5小题，满分39分）
21. 如图，，，直线与，的延长线分别交于点，．求证：．
【答案】见解析
【解析】
【分析】根据已知条件，，得到，从而得到，即可证明．
【详解】证明：∵，
∴．
∵，
∴．
∴．
∴．
【点睛】本题考查平行线的性质和判定．平行线的性质：两直线平行，内错角相等．平行线的判定：同位角相等，两直线平行．
22. 一个两位数，个位数字与十位数字的和为8，个位数字与十位数字互换位置后，所得的两位数比原两位数小18，则原两位数是多少？
【答案】原两位数是53．
【解析】
【分析】设原两位数的个位数字为x，十位数字为y，根据“个位数字与十位数字的和为8，个位数字与十位数字互换位置后，所得的两位数比原两位数小18”，即可得出关于x，y的二元一次方程组，解之即可得出x，y的值，再将其代入10y＋x即可得出结论．
【详解】解：设原两位数的个位数字为x，十位数字为y，
根据题意得：
解得：
∴10y+x＝53．
答：原两位数是53．
【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
23. 已知弹簧秤内的弹簧在一定限度内，它的长度y（厘米）与所挂重物质量x（千克）是一次函数关系，其函数图象如图所示．
（1）写出y关于x的函数解析式；
（2）该弹簧秤挂上一个重物时，量出弹簧的长度是7.2厘米，那么这个重物的质量是多少千克？
【答案】（1）
（2）这个重物的质量是2千克．
【解析】
【分析】（1）根据待定系数法即可求解；
（2）把y=7.2代入即可求解．
【小问1详解】
设y关于x的函数解析式为y＝kx+b，
由题意，
解得，
∴所求的函数解析式为y＝x+6．
【小问2详解】
y＝7.2时， ，解得x＝2，
答：这个重物的质量是2千克．
【点睛】此题主要考查一次函数的实际应用，解题的关键是熟知待定系数法的运用．
24. 已知：如图，，，．
求证：．
证明：∵，
∴______（ ）．
∴（ ），
______（两直线平行，内错角相等）
∵，，
∴______．
∴（ ）．
∴（ ）．

【答案】；同旁内角互补，两直线平行；两直线平行，同位角相等；；；同位角相等，两直线平行；两直线平行，内错角相等
【解析】
【分析】根据平行线的判定与性质求解即可．
【详解】证明：∵，
∴（同旁内角互补，两直线平行）．
∴（两直线平行，同位角相等）．
（两直线平行，内错角相等）．
∵，（已知）
∴．
∴（同位角相等，两直线平行）．
∴（两直线平行，内错角相等）．
故答案为：；同旁内角互补，两直线平行；两直线平行，同位角相等；；；同位角相等，两直线平行；两直线平行，内错角相等．
【点睛】此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．
25. 随着新冠疫情的出现，口罩成为日常生活的必需品，某医药公司每月生产甲、乙两种型号的防疫口罩共20万只，且所有口罩当月全部卖出，其中成本、售价如表：
（1）若该公司三月份的利润为8.8万元，求生产甲、乙两种型号的防疫口罩分别是多少万只？
（2）某同学有16.2元的零花钱，打算购买甲和乙两种口罩，正好赶上口罩价格调整，其中甲型口罩售价上涨50%，乙型口罩按原价出售，则该同学有多少种不同的购买方案可以使钱正好花完？请设计出来．
【答案】（1）该公司三月份生产甲种型号的防疫口罩12万只，乙种型号的防疫口罩8万只
（2）该同学共有2种购买方案，方案1：购买4个甲型口罩，9个乙型口罩；方案2：购买2个甲型口罩，18个乙型口罩．
【解析】
【分析】（1）设该公司三月份生产甲种型号的防疫口罩x万只，乙种型号的防疫口罩y万只，根据该公司三月份生产甲、乙两种型号的防疫口罩共20万只且全部售出后获得的总利润为8.8万元，可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）设该同学购买m只甲型口罩，n只乙型口罩，利用总价=单价×数量，可得出关于m，n的二元一次方程，结合m，n均为正整数，即可得出各购买方案．
【小问1详解】
设该公司三月份生产甲种型号的防疫口罩x万只，乙种型号的防疫口罩y万只，根据题意得：
，
解得：．
答：该公司三月份生产甲种型号的防疫口罩12万只，乙种型号的防疫口罩8万只；
【小问2详解】
设该同学购买m只甲型口罩，n只乙型口罩，根据题意得：
，
∴，
又∵m，n均为正整数，
∴或，
∴该同学共有2种购买方案，
方案1：购买4个甲型口罩，9个乙型口罩；
方案2：购买2个甲型口罩，18个乙型口罩．
【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）找准等量关系，正确列出二元一次方程．
五、附加题（10分）
26. 直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！
问题探究】


（1）①如图1，若，点P在内部，，则 ；
②如图2，若，将点P在外部，求之间数量关系 （不需证明）；
③如图3，写出之间的数量关系： （不需证明）．
【变式拓展】
（2）如图4，五角星，请直接写出 ．
（3）如图5，将五角星去掉一个角后，是多少？请证明你的结论．
【答案】（1）①；②；③；（2）；（3），证明见解析
【解析】
【分析】（1）①过点P作，利用平行线的性质可得，则；②根据平行线的性质的，再根据三角形外角的性质即可得到；③延长交于点E，利用三角形外角的性质即可得到；
（2）根据三角形外角的性质可得，进而根据三角形内角和定理得到；
（3）连接，先根据三角形内角和定理证明，再由，即可得到．
【详解】解：（1）①如图1，过点P作，
∵，
∴，
∴，
∴，
故答案为：；

②如图2，
∵，
∴，
又∵，
∴，
故答案为：；

③如图3，延长交于点E，
∵，
∴，
∴，
故答案为：；

（2）如图4，
∵，
又∵，
∴，
故答案为：；

（3），证明如下：
如图5，连接，
∵，
∴，
∵，
∴．
【点睛】本题主要考查了三角形内角和定理，三角形外角的性质，平行线的性质等等，灵活运用所学知识是解题的关键．
甲
乙
成本
12元/只
0.4元/只
售价
1.8元/只
0.6元/只