2024年新高考数学一轮复习知识梳理与题型归纳第13讲函数模型及其应用（学生版）

这是一份2024年新高考数学一轮复习知识梳理与题型归纳第13讲函数模型及其应用（学生版），共6页。试卷主要包含了几种常见的函数模型等内容，欢迎下载使用。

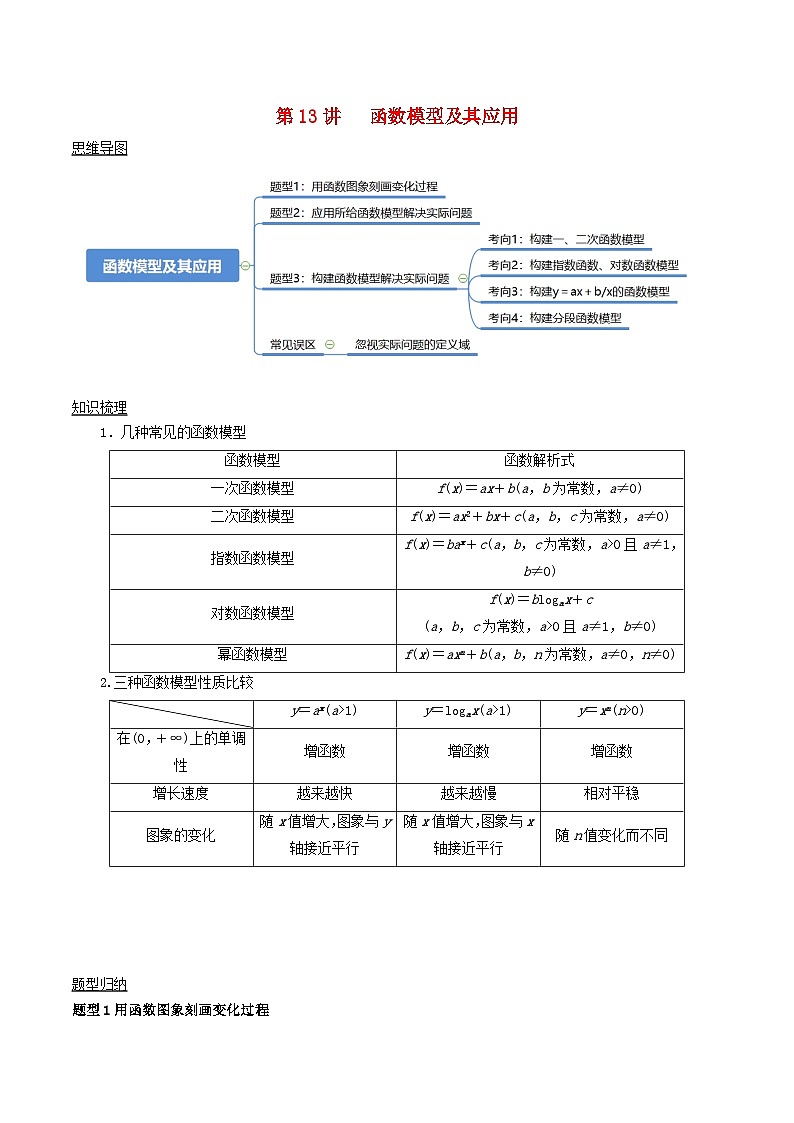
知识梳理
1．几种常见的函数模型
2.三种函数模型性质比较
题型归纳
题型1用函数图象刻画变化过程
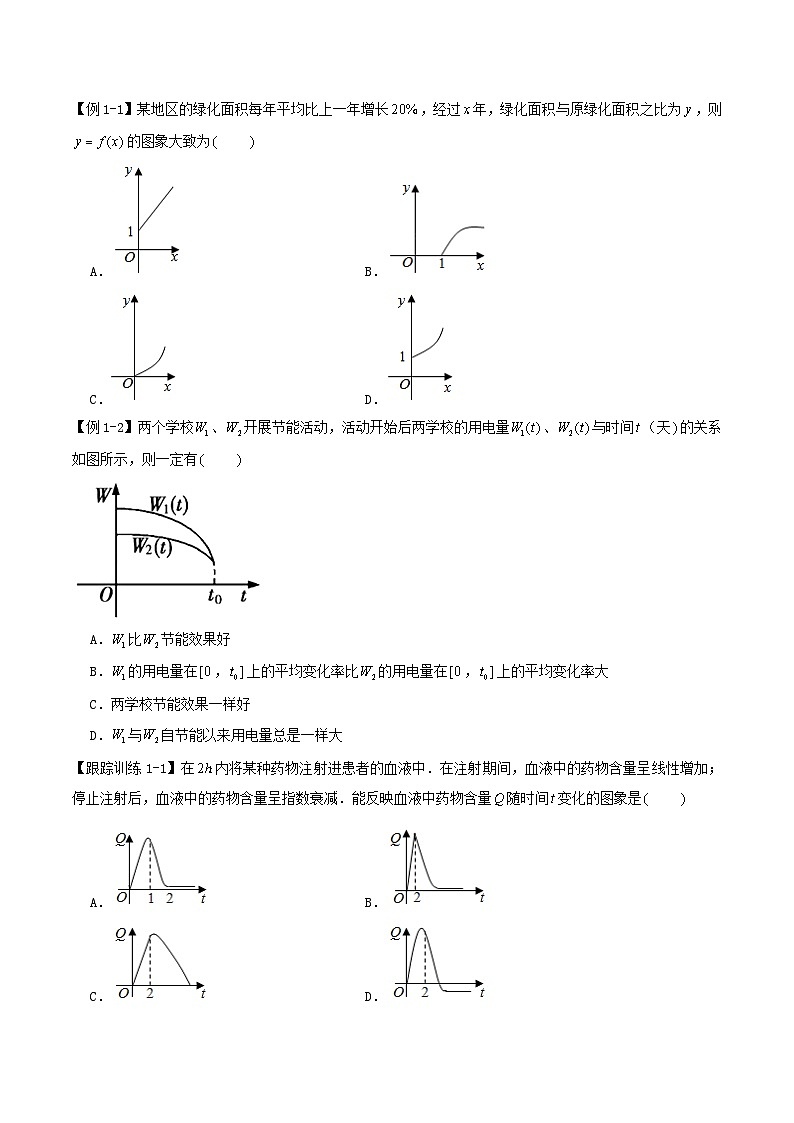
【例1-1】某地区的绿化面积每年平均比上一年增长，经过年，绿化面积与原绿化面积之比为，则的图象大致为
A．B．
C．D．
【例1-2】两个学校、开展节能活动，活动开始后两学校的用电量、与时间（天的关系如图所示，则一定有
A．比节能效果好
B．的用电量在，上的平均变化率比的用电量在，上的平均变化率大
C．两学校节能效果一样好
D．与自节能以来用电量总是一样大
【跟踪训练1-1】在内将某种药物注射进患者的血液中．在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减．能反映血液中药物含量随时间变化的图象是
A．B．
C．D．
【跟踪训练1-2】近两年为抑制房价过快上涨，政府出台了系列以“限购、限外、限贷、限价”为主题的房地产调控政策．各地房产部门为尽快实现稳定房价，提出多种方案，其中之一就是在规定的时间内完成房产供应量任务．已知房产供应量与时间的函数关系如图所示，则在以下四种房产供应方案中，供应效率（单位时间的供应量）逐步提高的是
A．B．
C．D．
【名师指导】
判断函数图象与实际问题中两变量变化过程相吻合的两种方法
(1)构建函数模型法：当根据题意易构建函数模型时，先建立函数模型，再结合模型选图象．
(2)验证法：当根据题意不易建立函数模型时，则根据实际问题中两变量的变化特点，结合图象的变化趋势，验证是否吻合，从中排除不符合实际的情况，选择出符合实际情况的答案．
题型2应用所给函数模型解决实际问题
【例2-1】基本再生数与世代间隔是新冠肺炎的流行病学基本参数．基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型：描述累计感染病例数随时间（单位：天）的变化规律，指数增长率与，近似满足．有学者基于已有数据估计出，．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为
A．1.2天B．1.8天C．2.5天D．3.5天
【例2-2】模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数的单位：天）的模型：，其中为最大确诊病例数．当时，标志着已初步遏制疫情，则约为
A．60B．63C．66D．69
【跟踪训练2-1】尽管目前人类还无法准确预报地震，但科学家通过研究发现地震释放出的能量（单位：焦耳）与地震里氏震级之间的关系为，1976年7月28日我国唐山发生的里氏7.8级地震与2008年5月12日我国汶川发生的里氏8.0级地震所释放出来的能量的比值为
A．B．0.3C．D．
【跟踪训练2-2】某食品的保鲜时间（单位：小时）与储存温度（单位：满足函数关系为自然对数的底数，，为常数），若该食品在的保鲜时间是384小时，在的保鲜时间是24小时，则该食品在的保鲜时间是 ．
【名师指导】
求解所给函数模型解决实际问题的关注点
(1)认清所给函数模型，弄清哪些量为待定系数．
(2)根据已知利用待定系数法，确定模型中的待定系数．
(3)利用该模型求解实际问题．
题型3构建函数模型解决实际问题
【例3-1】某公司生产某种产品，其年产量为万件时利润为万元，当时，年利润为，当时，年利润为．
（1）若公司生产量在且年利润不低于400万时，求生产量的范围；
（2）求公司年利润的最大值．
【例3-2】一片森林原来面积为a，计划每年砍伐一些树，且每年砍伐面积的百分比相等，当砍伐到面积的一半时，所用时间是10年，为保护生态环境，森林面积至少要保留原面积的eq \f(1,4)，已知到今年为止，森林剩余面积为原来的eq \f(\r(2),2).
(1)求每年砍伐面积的百分比；
(2)到今年为止，该森林已砍伐了多少年？
【例3-3】某地区要建造一条防洪堤，其横断面为等腰梯形，腰与底边夹角为60°(如图)，考虑防洪堤坚固性及石块用料等因素，设计其横断面要求面积为9eq \r(3) 平方米，且高度不低于eq \r(3) 米．记防洪堤横断面的腰长为x米，外周长(梯形的上底线段BC与两腰长的和)为y米．要使防洪堤的上面与两侧面的水泥用料最省(即横断面的外周长最小)，则防洪堤的腰长x＝________米．
【例3-4】济南新旧动能转换先行区，承载着济南从“大明湖时代”迈向“黄河时代”的梦想，肩负着山东省新旧动能转换先行先试的重任，是全国新旧动能转换的先行区．先行区将以“结构优化、质量提升”为目标，通过开放平台汇聚创新要素，坚持绿色循环保障持续发展，建设现代绿色智慧新城．2019年某智能机器人制造企业有意落户先行区，对市场进行了可行性分析，如果全年固定成本共需2000（万元），每年生产机器人x（ 百个），需另投人成本C（x）（万元），且，由市场调研知，每个机器人售价6万元，且全年生产的机器人当年能全部销售完．
（1）求年利润L（x）（万元）关于年产量x（ 百个）的函数关系式；（利润＝销售额﹣成本）
（2）该企业决定：当企业年最大利润超过2000（万元）时，才选择落户新旧动能转换先行区．请问该企业能否落户先行区，并说明理由．
【跟踪训练3-1】在天文学中，天体的明暗程度可以用星等或亮度来描述．若两颗星的星等与亮度满足．其中星等为，星的亮度为．
（1）若，则 ；
（2）若太阳的星等是，天狼星的星等是，则太阳与天狼星的亮度的比值为 ．
【跟踪训练3-2】某餐厅经营盒饭生意，每天的房租、人员工资等固定成本为200元，每盒盒饭的成本为15元，销售单价与日均销售量的关系如表：
根据以上数据，当这个餐厅每盒盒饭定价______元时，利润最大（ ）
A．16.5B．19.5C．21.5D．22
【跟踪训练3-3】某地某路无人驾驶公交车发车时间间隔t（单位：分钟）满足5≤t≤20，t∈N．经测算，该路无人驾驶公交车载客量p（t）与发车时间间隔t满足：其中t∈N．
（1）求p（5），并说明p（5）的实际意义；
（2）若该路公交车每分钟的净收益（元），问当发车时间间隔为多少时，该路公交车每分钟的净收益最大？并求每分钟的最大净收益．函数模型
函数解析式
一次函数模型
f(x)＝ax＋b(a，b为常数，a≠0)
二次函数模型
f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)
指数函数模型
f(x)＝bax＋c(a，b，c为常数，a>0且a≠1，b≠0)
对数函数模型
f(x)＝blgax＋c
(a，b，c为常数，a>0且a≠1，b≠0)
幂函数模型
f(x)＝axn＋b(a，b，n为常数，a≠0，n≠0)
y＝ax(a>1)
y＝lgax(a>1)
y＝xn(n>0)
在(0，＋∞)上的单调性
增函数
增函数
增函数
增长速度
越来越快
越来越慢
相对平稳
图象的变化
随x值增大，图象与y轴接近平行
随x值增大，图象与x轴接近平行
随n值变化而不同
单价/元
16
17
18
19
20
21
22
日销售量/盒
480
440
400
360
320
280
240