第3章函数与基本初等函数第3节函数的奇偶性与周期性2025届高考数学一轮总复习(适用于新高考新教材)ppt

展开

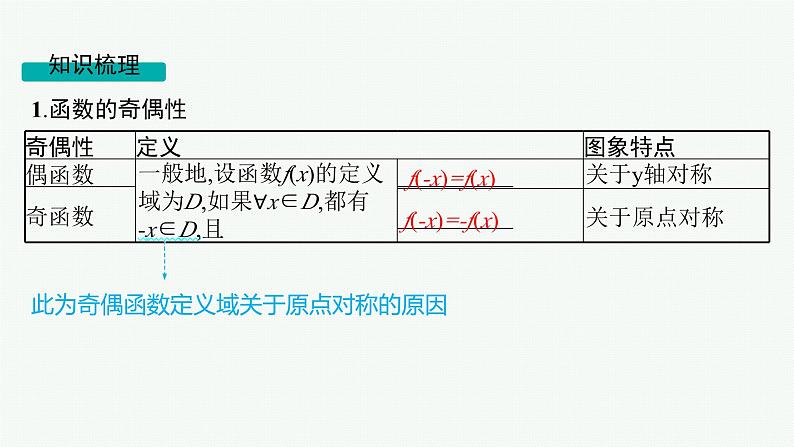
这是一份第3章函数与基本初等函数第3节函数的奇偶性与周期性2025届高考数学一轮总复习(适用于新高考新教材)ppt，共36页。PPT课件主要包含了目录索引，函数的奇偶性，BCD，变式探究1，-x2-x等内容，欢迎下载使用。

研考点精准突破
强基础固本增分
此为奇偶函数定义域关于原点对称的原因
f(-x)=f(x)
f(-x)=-f(x)
微思考存在既是奇函数又是偶函数的函数吗?唯一吗?
2.函数的周期性(1)周期函数:一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D都有x+T∈D,且f(x+T)=__________,那么函数f(x)就叫做周期函数.非零常数__________就叫做这个函数的周期. (2)最小正周期:如果在周期函数f(x)的所有周期中存在一个__________的正数,那么这个最小正数就叫做f(x)的最小正周期.
并非所有周期函数都有最小正周期
微点拨若T是函数f(x)的周期,那么nT(n∈Z,n≠0)也是函数f(x)的周期.
常用结论1.关于函数奇偶性的常用结论(1)如果函数f(x)是奇函数且在x=0处有定义,那么一定有f(0)=0;如果函数f(x)是偶函数,那么f(-x)=f(x)=f(|x|).(2)如果函数f(x)不是常数函数,当f(x)是奇函数时,它在两个对称的区间上具有相同的单调性;当f(x)是偶函数时,它在两个对称的区间上具有相反的单调性.(3)奇函数的导数是偶函数,偶函数的导数是奇函数.(4)如果f(x)=g(x)+m(m为常数)且g(x)为奇函数,那么f(x)+f(-x)=2m.(5)如果奇函数f(x)存在最大值与最小值,那么它的最大值与最小值之和等于零.
题组二回源教材5.(人教B版必修第一册习题3-1B第8题改编)已知函数f(x)=(x-1)2+ax+2是偶函数,则实数a=__________.
6.(人教A版必修第一册习题3.2第11题改编)已知函数f(x)是定义域为R的奇函数,当x≥0时,f(x)=x(1+x),则f(x)的解析式为____________________.
解析由于f(x)=(x-1)2+ax+2=x2+(a-2)x+3,而f(x)是偶函数,所以a-2=0,解得a=2.
考点一函数奇偶性的判断
解析易知函数f(x),g(x)分别为奇函数和偶函数.由于f(-x)+g(-x)=-f(x)+g(x),所以f(x)+g(x)是非奇非偶函数,故A选项错误;由于f(-x)·g(-x)=-f(x)·g(x),所以f(x)·g(x)是奇函数,故B选项正确;由于|f(-x)|-g(-x)=|-f(x)|-g(x)=|f(x)|-g(x),所以|f(x)|-g(x)是偶函数,故C选项正确;由于g[f(-x)]=g[-f(x)]=g[f(x)],所以g[f(x)]是偶函数,故D选项正确,故选BCD.
解 ①函数的定义域为{x|x≠2},关于原点不对称,所以f(x)为非奇非偶函数;②由4-x2>0得-20时,f(x)=-x2+2x+1,而-x<0,所以f(-x)=(-x)2+2(-x)-1=x2-2x-1=-f(x);当x<0时,f(x)=x2+2x-1,而-x>0,所以f(-x)=-(-x)2+2(-x)+1=-x2-2x+1=-f(x),所以当x∈(-∞,0)∪(0,+∞)时,都有f(-x)=-f(x),即函数为奇函数.
规律方法奇偶性判断方法(1)定义法
(2)图象法(3)性质法:若f(x),g(x)有相同的定义域,则
考点二函数奇偶性的应用(多考向探究预测)
所以g(x)为奇函数,因为f(a)=g(a)+1=5,所以g(a)=4,所以f(-a)=g(-a)+1=-g(a)+1=-3,即f(-a)=-3,故选D.
变式探究2在本例(2)中,若函数解析式不变,且已知该函数在区间[a,b]上的最大值为M,最小值为m,则M+m=__________.
规律方法利用奇偶性求解析式的方法技巧(1)区间变换法:已知函数的奇偶性和给定区间 M上的解析式,求对称区间 N上的解析式时,先设x∈N,则有-x∈M,可求得f(-x)表达式,再根据函数奇偶性得f(-x)与f(x)的关系,从而得到f(x)表达式.(2)构造方程组法:若已知奇函数f(x)与偶函数g(x)满足的一个方程,可在方程中令-x替换x,然后将f(-x),g(-x)根据奇偶性转化为-f(x),g(x),这又得到一个f(x)与g(x)满足的方程,通过解方程组即可得到f(x),g(x)的解析式.
(2)(2024·安徽定远模拟)已知函数f(x)是定义在[-1,1]上的奇函数,当0≤x≤1时,f(x)=x(x-1),则当-1≤x<0时,f(x)=__________.
解析设-1≤x<0,则0<-x≤1,于是f(-x)=-x(-x-1)=x2+x,由于f(x)是定义在[-1,1]上的奇函数,所以f(x)=-f(-x)=-x2-x.
规律方法函数周期性的判定与应用(1)判定:由f(x+T)=f(x)可得函数为周期函数且周期为T,同时要熟记关于函数周期的几个常用结论,能够根据f(x+T)与f(x)的关系快速得到函数周期.(2)应用:周期性的应用主要有两个方面.①求值:借助周期将自变量的值转化为已知的函数值或转化到解析式已知的区间上,代入求值;②求解析式:求函数在某一区间上的解析式时,可先设自变量在该区间上,然后利用函数的周期将自变量的值转化到解析式已知的区间上,同时结合函数的奇偶性得到所求解析式.
[对点训练2](2024·江苏八市模拟)已知函数f(x)的定义域为R,y=f(x)+ex是偶函数,y=f(x)-3ex是奇函数,则f(x)的最小值为(　　)
考点三函数的周期性及其应用
变式探究本例(2)中,条件不变,则f(2 023)=__________.
所以f(x)是周期为4的周期函数,且当2

相关课件更多