第4章一元函数的导数及其应用 第3节利用导数研究函数的极值、最值 2025年高考总复习数学配人教版(适用于新高考新教材)ppt

这是一份第4章一元函数的导数及其应用 第3节利用导数研究函数的极值、最值 2025年高考总复习数学配人教版(适用于新高考新教材)ppt，共44页。PPT课件主要包含了强基础固本增分，研考点精准突破，目录索引，极值点是一个实数，连续不断，最大值，fafb，最小值，-∞0，题组三连线高考等内容，欢迎下载使用。

1.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.2.能利用导数求某些函数的极大值、极小值以及给定闭区间上不超过三次的多项式函数的最大值、最小值.3.体会导数与极值、最大(小)值的关系.
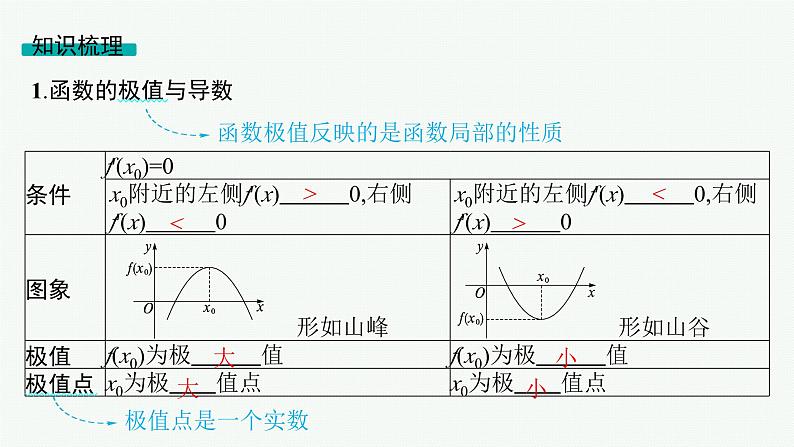
1.函数的极值与导数
函数极值反映的是函数局部的性质
微点拨对函数极值的理解(1)函数在一个区间的端点处一定不可能取得极值,即端点一定不是函数的极值点.(2)在一个给定的区间上,函数可能有若干个极值点,也可能不存在极值点;函数可以只有极大值没有极小值,或者只有极小值没有极大值,也可能既有极大值又有极小值.
微思考若函数f(x)可导,则当f'(x0)=0时,f(x)一定在x=x0处取得极值吗?
提示 不一定.f'(x0)=0是f(x)在x=x0处取得极值的必要不充分条件,例如f(x)=x3,满足f'(0)=0,但f(x)=x3在x=0处不取得极值.
2.函数的最值与导数
　反映的是函数整体的性质
(1)一般地,如果在区间[a,b]上函数y=f(x)的图象是一条　　　　　　的曲线,那么它必有最大值和最小值. (2)一般地,求函数y=f(x)在闭区间[a,b]上的最大值与最小值的步骤如下:①求函数y=f(x)在区间(a,b)上的　　　; ②将函数y=f(x)的各极值与端点处的函数值　　　　　比较,其中最大的一个是　　　　　　,最小的一个是　　　　　　. 
微点拨对函数最值的理解(1)函数在其定义域上或在某给定区间上若存在最大(小)值,则其具有唯一性,即只能有一个最大(小)值;(2)函数的最值可以在区间端点处取得,但极值不能在区间端点处取得;(3)函数有最值时,不一定有极值;有极值时,不一定有最值;(4)若f(x)在[a,b]上单调递增,则f(a),f(b)分别是f(x)在[a,b]上的最小值、最大值;若f(x)在[a,b]上单调递减,则f(a),f(b)分别是f(x)在[a,b]上的最大值、最小值.
常用结论1.有极值的函数一定不是单调函数.2.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),其导数f'(x)=3ax2+2bx+c,方程3ax2+2bx+c=0的判别式Δ=4b2-12ac,有以下结论:
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)1.一个函数的极大值一定比极小值大.(　　)2.函数在闭区间上的最值一定在端点处取得.(　　)3.函数在开区间上的最值一定是相应的极值.(　　)
题组二回源教材4.(人教B版选择性必修第三册6.2.2节练习B第3题改编)设函数f(x)=ax3+3x+2有极值,则实数a的取值范围是　　　　　　　,函数的极值点是　　　　. 
解析 当a=0时,f(x)=3x+2没有极值,不合题意;当a≠0时,f'(x)=3ax2+3,则f'(x)=3ax2+3=0应有两个不相等的实数根,所以Δ=-36a>0,解得a<0,此时f'(x)=0的根是x=± ,此即为极值点.
5.(人教A版选择性必修第二册5.3.2节例7改编)给定函数f(x)=(x+1)ex,则函数的最小值为　　　　. 
解析 由已知得f'(x)=(x+2)ex,令f'(x)=0,得x=-2,当x<-2时,f'(x)<0,f(x)单调递减,当x>-2时,f'(x)>0,f(x)单调递增,因此f(x)在x=-2处取得极小值f(-2)= ,所以由f(x)的图象(图略)可知,函数的最小值为 .
7.(2021·全国乙,文12)设a≠0,若x=a为函数f(x)=a(x-a)2(x-b)的极大值点,则(　　)A.abC.aba2
8.(2021·新高考Ⅰ,15)函数f(x)=|2x-1|-2ln x的最小值为　　　　　. 
考点一 利用导数研究函数的极值(多考向探究预测)
考向1求函数的极值(极值点)例1(1)(2024·浙江杭州模拟)设函数f(x)=2ln x-x2,则(　　)A.x=e为极大值点B.x=1为极大值点C.x=1为极小值点D.无极值点
时,f'(x)<0,当00,故f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,故x=1是极大值点,故选B.
01时,f'(x)>0,f(x)单调递增,所以当x=1时,函数f(x)取得极小值,且极小值f(1)=e-3,故选A.
考向2已知极值(极值点)求参数值(范围)例2(1)(2024·湖南长沙模拟)已知函数f(x)的导函数g(x)=(x-1)(x2-3x+a),若1不是函数f(x)的极值点,则实数a的值为(　　)A.-1B.0C.1D.2
解析 由题意f'(x)=g(x)=(x-1)(x2-3x+a),若1不是函数f(x)的极值点,设h(x)=x2-3x+a,则h(1)=0,即1-3+a=0⇒a=2,当a=2时,f'(x)=(x-1)(x2-3x+2)=(x-1)2(x-2),故当x>2时,f'(x)>0;当x<2且x≠1时,f'(x)<0,因此x=2是f(x)的极值点,1不是极值点,所以a=2满足题意,故选D.
(2)(2024·安徽合肥模拟)函数f(x)=x3+3ax2+bx+a2在x=-1处有极小值0,则a+b=(　　)A.7B.6C.5D.11
解析 因为f(x)=x3+3ax2+bx+a2,所以f'(x)=3x2+6ax+b,由题意可知
当a=1,b=3时,f'(x)=3x2+6x+3=3(x+1)2≥0,函数f(x)为R上的增函数,此时f(x)无极值,不合题意;当a=2,b=9时,f'(x)=3x2+12x+9=3(x+1)(x+3),令f'(x)>0,得x<-3或x>-1,令f'(x)<0,得-3(3)(多选题)(2023·新高考Ⅱ,11)若函数f(x)=aln x+ (a≠0)既有极大值也有极小值,则(　 　)A.bc>0B.ab>0C.b2+8ac>0D.ac<0
变式探究1(变条件)本例(1)中,其他条件不变,将“若1不是函数f(x)的极值点”改为“若-1是函数f(x)的极值点”,则实数a的值为　　　　. 
解析 由于-1是函数f(x)的极值点,所以f'(-1)=g(-1)=0,即(-1-1)(1+3+a)=0,解得a=-4,此时f'(x)=(x-1)(x2-3x-4)=(x-1)(x+1)(x-4),经验证符合题意,故实数a的值为-4.
变式探究2(变条件变结论)本例(1)中,其他条件不变,将“若1不是函数f(x)的极值点”改为“若1是函数f(x)的极大值点”,则实数a的取值范围为　　　　. 
解析 由题意f'(x)=(x-1)(x2-3x+a),令h(x)=x2-3x+a,当h(x)≥0恒成立时,有Δ=9-4a≤0,则a ,此时,若x∈(-∞,1),则f'(x)<0,若x∈(1,+∞),则f'(x)>0,所以1是f(x)的极小值点,不合题意;设h(x)=x2-3x+a=0的两个实数根分别为x1,x2,且x10,当x∈(1,x2)时,f'(x)<0,所以x=1是f(x)的极大值点,符合题意.所以实数a的取值范围为(-∞,2).
考点二利用导数研究函数的最值(多考向探究预测)
考向1求函数的最值例3(1)(2024·北京石景山区模拟)已知x=1是函数f(x)=ax3-3x的一个极值点,其中a为实数,则f(x)在区间[-2,2]上的最大值为(　　)A.0B.1C.2D.3
解析 f'(x)=3ax2-3,因为x=1是y=f(x)的一个极值点,所以f'(1)=3a-3=0,解得a=1,则f'(x)=3x2-3=3(x-1)(x+1),x∈[-2,2].当x∈(-2,-1)时,f'(x)>0,f(x)单调递增;当x∈(-1,1)时,f'(x)<0,f(x)单调递减;当x∈(1,2)时,f'(x)>0,f(x)单调递增,符合题意,所以当x=-1时,函数f(x)取得极大值,极大值为f(-1)=-1+3=2,又f(2)=23-3×2=2,所以函数f(x)在[-2,2]上的最大值为2,故选C.
(2)(2024·河北邢台模拟)函数f(x)= +x-ln x的最小值为(　　)A.eB.e+1C.1D.e-1
x>0,所以ex+x>0,当x∈(0,1)时,f'(x)<0,即f(x)在(0,1)内单调递减,当x∈(1,+∞)时,f'(x)>0,即f(x)在(1,+∞)上单调递增,所以f(x)在x=1处取得极小值且极小值为最小值,故f(x)的最小值为f(x)min=f(1)=e+1,故选B.
考向2根据函数的最值求参数值(范围)
[对点训练1](2024·山东省实验中学检测)若函数f(x)= x3+x2-2在区间(a-4,a)上存在最小值,则整数a的取值集合是　　　　　　　　. 
因为函数f(x)在区间(a-4,a)上存在最小值,
解得1≤a<4,所以整数a的取值集合为{1,2,3}.
考点三 利用导数解决实际问题
例5(2024·陕西西安模拟)从商业化书店到公益性城市书房,再到“会呼吸的文化森林”——图书馆,建设高水平、现代化、开放式的图书馆一直是大众的共同心声.现有一块不规则的地,其平面图形如图1所示,AC=8,建立如图2所示的平面直角坐标系,将曲线AB看成函数f(x)= 图象的一部分,BC为一次函数图象的一部分,若在此块地上建立一座图书馆,平面图为直角梯形CDEF(如图2),则图书馆占地面积的最大值为(　　)
设线段BC对应的函数解析式为y=mx+n(4≤x≤8),因为直线BC经过点B(4,4),C(8,0),所以m=-1,n=8,所以y=-x+8(4≤x≤8).
[对点训练2](2024·福建厦门模拟)某城市举办花市,如图,有一块半径为20米,圆心角∠AOB= 的扇形展示台,展示台分成了四个区域:三角形OCD摆放菊花“泥金香”,弓形CMD摆放菊花“紫龙卧雪”,扇形AOC和扇形BOD(其中∠AOC=∠BOD)摆放菊花“朱砂红霜”.预计这三种菊花展示带来的日效益分别是:泥金香50元/平方米,紫龙卧雪30元/平方米,朱砂红霜40元/平方米,则当∠COD=　　　　时,日效益总量达到最大值.