



所属成套资源:中考数学二轮重难点复习讲义(2份打包,原卷版+解析版)
中考数学二轮重难点复习讲义模型37 四边形对角互补模型(2份打包,原卷版+解析版)
展开
这是一份中考数学二轮重难点复习讲义模型37 四边形对角互补模型(2份打包,原卷版+解析版),文件包含中考数学二轮重难点复习讲义模型37四边形对角互补模型原卷版doc、中考数学二轮重难点复习讲义模型37四边形对角互补模型解析版doc等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
对角互补模型:即四边形或多边形构成的几何图形中,相对的角互补。主要分为含90°与120°的两种对角互补类型。该题型常用到的辅助线主要是顶定点向两边做垂线,从而证明两个三角形全等或者相似.
模型一、含90°的全等型
1.如图,已知∠AOB=∠DCE=90º,OC平分∠AOB.
则可以得到如下几个结论:①CD=CE,②OD+OE= SKIPIF 1 < 0 OC,
③ SKIPIF 1 < 0 .
2.如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90º,OC平分
∠AOB.
则可得到如下几个结论:①CD=CE,②OE-OD= SKIPIF 1 < 0 OC,③ SKIPIF 1 < 0 .
模型二、 含60°与120°的全等型
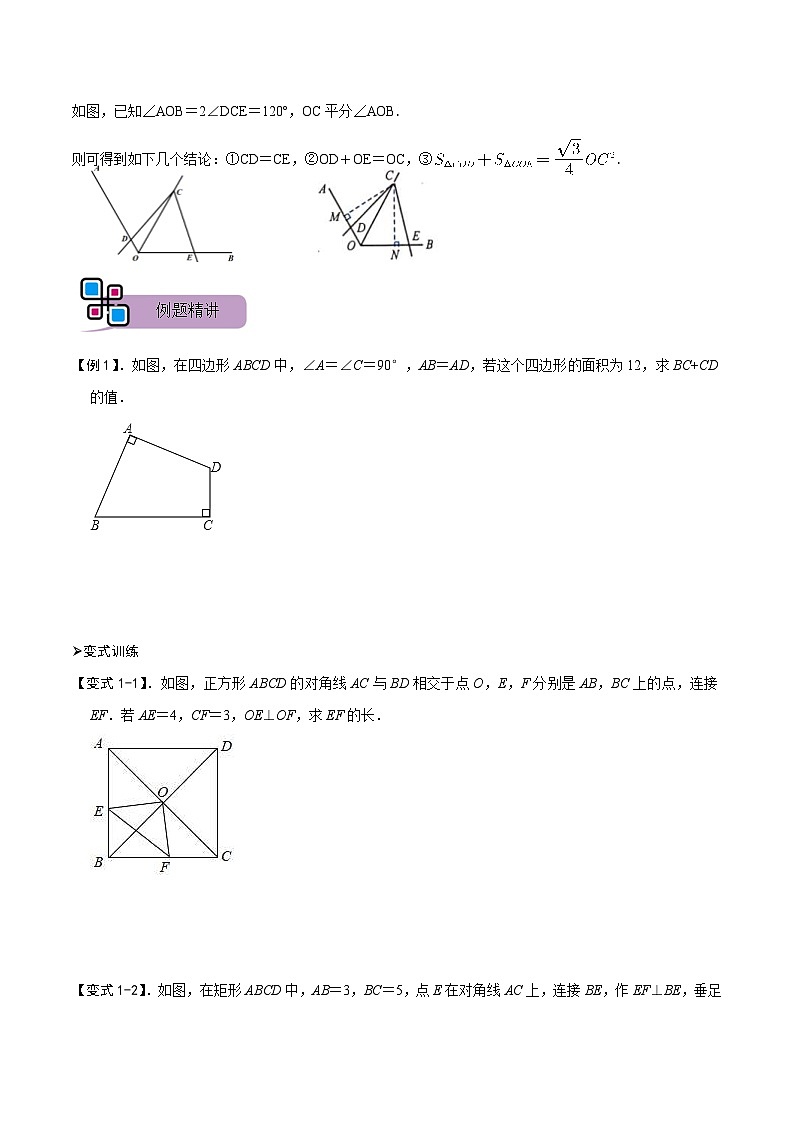
如图,已知∠AOB=2∠DCE=120º,OC平分∠AOB.
则可得到如下几个结论:①CD=CE,②OD+OE=OC,③ SKIPIF 1 < 0 .
例题精讲
【例1】.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,求BC+CD的值.
变式训练
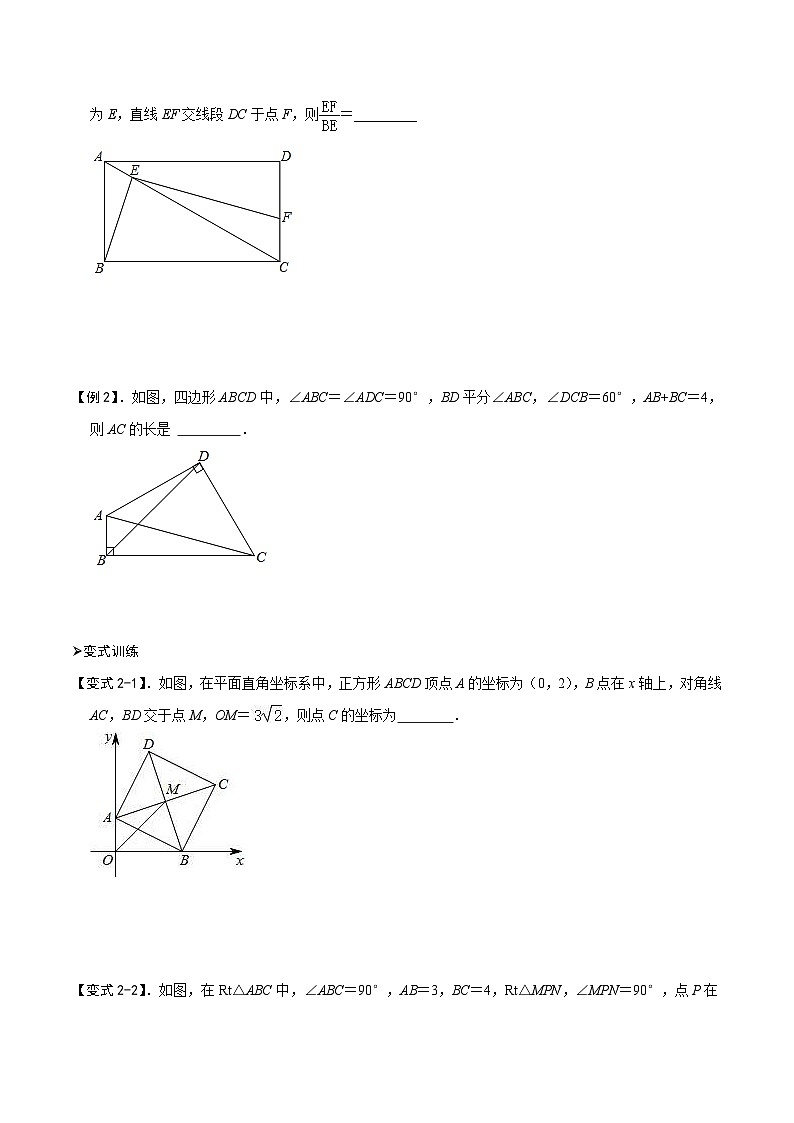
【变式1-1】.如图,正方形ABCD的对角线AC与BD相交于点O,E,F分别是AB,BC上的点,连接EF.若AE=4,CF=3,OE⊥OF,求EF的长.
【变式1-2】.如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=_________
【例2】.如图,四边形ABCD中,∠ABC=∠ADC=90°,BD平分∠ABC,∠DCB=60°,AB+BC=4,则AC的长是 .
变式训练
【变式2-1】.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点在x轴上,对角线AC,BD交于点M,OM=,则点C的坐标为 .
【变式2-2】.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= .
【变式2-3】.如图,正方形ABCD,点P是对角线AC上一点,连接BP,过P作PQ⊥BP,PQ交CD于Q,连接BQ交AC于G,若AP=,Q为CD中点,则下列结论:
①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形ABCD的面积是16;
其中正确结论是_________
1.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD= .
2.如图,在△ABC中,∠ABC=60°,AB=2,BC=8,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为 .
3.如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
4.四边形ABCD被对角线BD分为等腰直角△ABD和直角△CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.
5.如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,证明:无论正方形OMNP旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值.
6.基本模型
在任意四边形中,出现一组对角互补,则为对角互补模型.
解题思路:
1.过互补角的顶点作旋转构造全等或相似;
2过互补角的顶点作双垂线构造全等或相似.
问题:
如图,在四边形ABCD中,∠ABC=∠ADC=90°,BD平分∠ABC.
结论:①AD=CD;②AB+BC=BD;③S四边形ABCD=BD2
请证明【基本模型】中的结论.
求证:①AD=CD;②AB+BC=BD;③S四边形ABCD=BD2.
7.如图1,∠AOB=90°,OC平分∠AOB,以C为顶点作∠DCE=90°,交OA于点D,OB于点E.
(1)求证:CD=CE;
(2)图1中,若OC=3,求OD+OE的长;
(3)如图2,∠AOB=120°,OC平分∠AOB,以C为顶点作∠DCE=60°,交OA于点D,OB于点E.若OC=3,求四边形OECD的面积.
8.感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)
探究:
9.问题提出:
(1)如图1,已知线段AB=2,AC=4,连接BC,则三角形ABC面积最大为 ;
问题探究:
(2)如图2,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,若CD+BC=10,求四边形ABCD的面积;
问题解决:
(3)在四边形ABCD中,AB=AD,∠BAD+∠BCD=180°,AC=8,求四边形ABCD面积的最大值.
10.定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形ABCD中,∠A与∠C是一组对角,若∠B:∠C:∠D=2:3:4,则∠A= °;
②如图1,在△ABC中,点D,E分别在边AB,BC上,且BE•BC=AB•BD,求证:四边形ADEC是互补四边形.
(2)探究发现:如图2,在等腰△ABE中,AE=BE,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,求证:∠ABD=∠BAC=∠E.
11.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系;
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是 ;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
12.【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等边△AMN,连接CN.求证:BM=CN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,AB=6,AC=4,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连接CN.试探究BM与CN的数量关系,并说明理由.
13.定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有 ;
(2)性质探究:
①如图1,四边形ABCD是奇异四边形,AB=AD,求证:CA平分∠BCD;
②如图2,四边形ABCD是奇异四边形,AB=AD,∠BCD=2α,试说明:csα=;
(3)性质应用:
如图3,四边形ABCD是奇异四边形,四条边中仅有BC=CD,且四边形ABCD的周长为6+2,∠BAC=45°,AC=3,求奇异四边形ABCD的面积.
14.已知:在四边形ABCD中,∠A+∠C=180°,DB平分∠ADC.
(1)求证:AB=BC;
(2)如图2,若∠ADB=60°,试判断△ABC的形状,并说明理由;
(3)如图3,在(2)得条件下,在AB上取一点E,BC上取一点F,连接CE、AF交于点M,连接EF,若∠CMF=60°,AD=EF=7,CD=8(CF>BF),求AE的长.
15.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB.
(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
16.如图,已知∠DCE与∠AOB,OC平分∠AOB.
(1)如图1,∠DCE与∠AOB的两边分别相交于点D、E,∠AOB=∠DCE=90°,试判断线段CD与CE的数量关系,并说明理由.
以下是小宇同学给出如下正确的解法:
解:CD=CE.
理由如下:如图1,过点C作CF⊥OC,交OB于点F,则∠OCF=90°,…
请根据小宇同学的证明思路,写出该证明的剩余部分.
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
(3)若∠AOB=120°,∠DCE=60°.
①如图3,∠DCE与∠AOB的两边分别相交于点D、E时,(1)中的结论成立吗?为什么?
线段OD、OE、OC有什么数量关系?说明理由.
②如图4,∠DCE的一边与AO的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段OD、OE、OC有什么数量关系;如图5,∠DCE的一边与BO的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段OD、OE、OC有什么数量关系.
17.在⊙O中,弦CD平分圆周角∠ACB,连接AB,过点D作DE∥AB交CB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若tan∠CAB=,且B是CE的中点,⊙O的直径是,求DE的长.
(3)P是弦AB下方圆上的一个动点,连接AP和BP,过点D作DH⊥BP于点H,请探究点P在运动的过程中,
的比值是否改变,若改变,请说明理由;若不变,请直接写出比值.
18.(1)探究:如图1,在△ABC和△ADE都是等边三角形,点D在边BC上.
①求∠DCE的度数;
②直接写出线段CD,CE,AC之间的数量关系;
(2)应用:如图2,在四边形ABCD中,AB=BC,∠ABC=60°,P是四边形ABCD内一点,且∠APC=120°,求证:PA+PC+PD≥BD;
(3)拓展;如图3,在平面直角坐标系中,点A的坐标为(﹣4,0),点B是y轴上一个动点,以AB为边在AB的下方作等边△ABC,求OC的最小值.
19.有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.
(1)如图1,在等邻边互补四边形ABCD中,AD=CD,且AD∥BC,BC=2AD,求∠B的度数;
(2)如图2,四边形ABCD内接于⊙O,连接DO交AC于点E(不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;
(3)在(2)的条件下,延长DO交BC于点F,交⊙O于点G,若=,tan∠ABC=,AC=12,求FG的长;
(4)如图3,四边形ABCD内接于⊙O,AB=BC,BD为⊙O的直径,连接AO并延长交BC于点E,交⊙O于点F,连接FC,设tan∠BAF=x,=y,求y与x之间的函数关系式.
相关试卷
这是一份模型37 四边形对角互补模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型37四边形对角互补模型原卷版docx、模型37四边形对角互补模型解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
这是一份中考数学二轮复习几何模型归纳讲练专题17 全等与相似模型-对角互补模型(2份打包,原卷版+教师版),文件包含中考数学二轮复习几何模型归纳讲练专题17全等与相似模型-对角互补模型原卷版doc、中考数学二轮复习几何模型归纳讲练专题17全等与相似模型-对角互补模型教师版doc等2份试卷配套教学资源,其中试卷共74页, 欢迎下载使用。
这是一份中考数学二轮复习几何模型重点突破讲练专题22 对角互补模型(2份打包,原卷版+教师版),文件包含中考数学二轮复习几何模型重点突破讲练专题22对角互补模型原卷版doc、中考数学二轮复习几何模型重点突破讲练专题22对角互补模型教师版doc等2份试卷配套教学资源,其中试卷共10页, 欢迎下载使用。









