



模型37 四边形对角互补模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用)
展开对角互补模型:即四边形或多边形构成的几何图形中,相对的角互补。主要分为含90°与120°的两种对角互补类型。该题型常用到的辅助线主要是顶定点向两边做垂线,从而证明两个三角形全等或者相似.
模型一、含90°的全等型
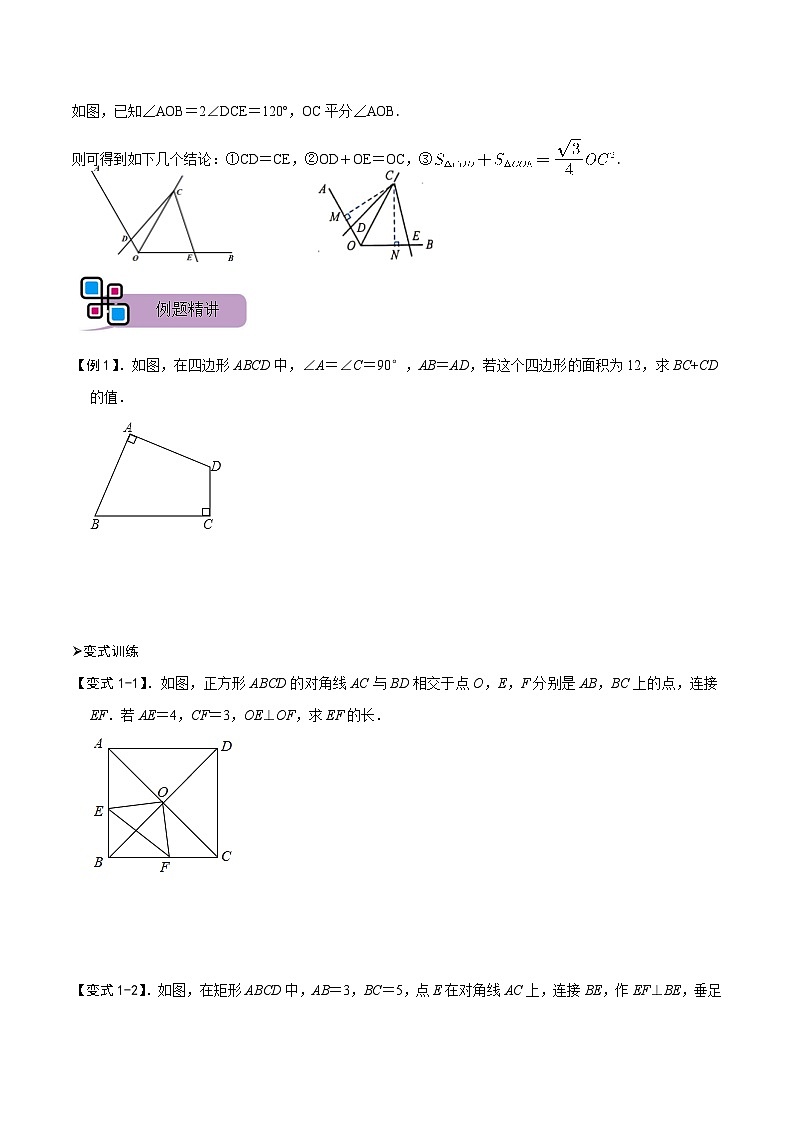
1.如图,已知∠AOB=∠DCE=90º,OC平分∠AOB.
则可以得到如下几个结论:①CD=CE,②OD+OE=OC,
③.
2.如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90º,OC平分
∠AOB.
则可得到如下几个结论:①CD=CE,②OE-OD=OC,③.
模型二、 含60°与120°的全等型
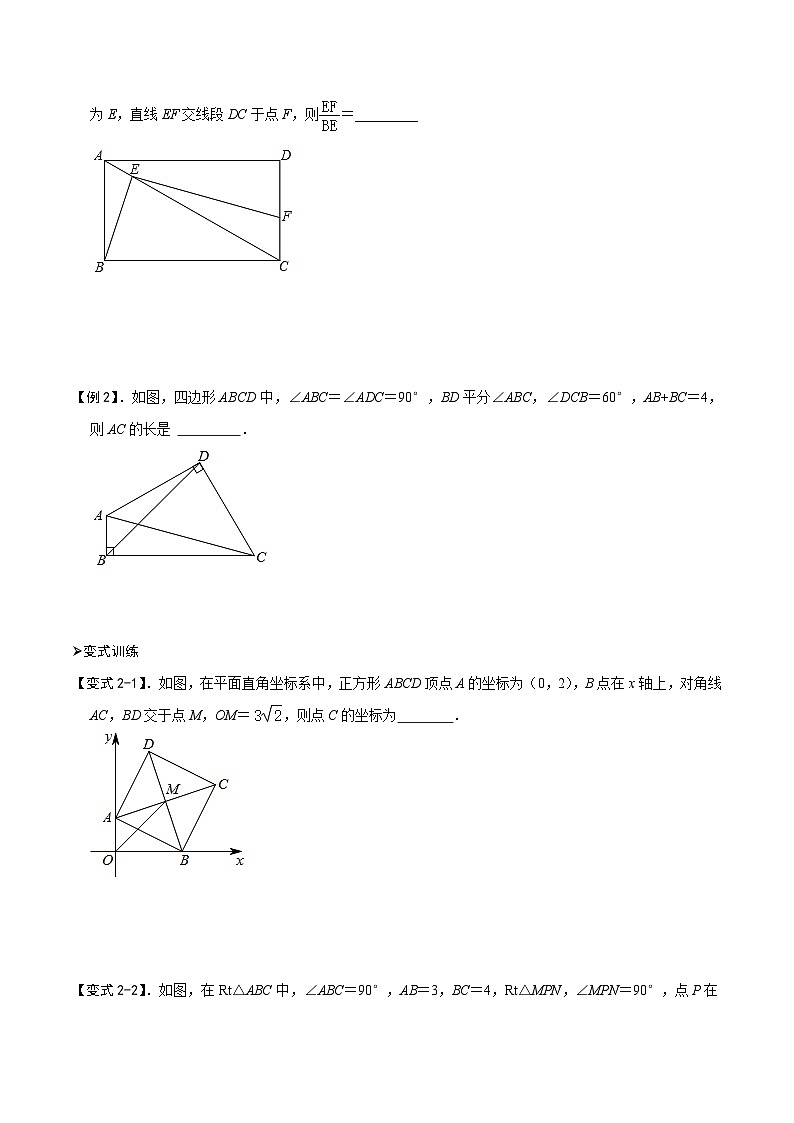
如图,已知∠AOB=2∠DCE=120º,OC平分∠AOB.
则可得到如下几个结论:①CD=CE,②OD+OE=OC,③.
例题精讲
【例1】.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,求BC+CD的值.
解:延长CB到E,使BE=DC,连接AE,AC,
∵∠ABE=∠BAC+∠ACB,
∠D=180°﹣∠DAC﹣∠DCA,
∵∠BAD=90°,∠BCD=90°,
∴∠BAC+∠ACB=90°+90°﹣∠DAC﹣∠DCA=180°﹣∠DAC﹣∠DCA,
∴∠ABE=∠D,
又∵BE=DC,AB=AD,
∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,
∴S△AEC=AE2=EC2,
∵S△AEC=S四边形ABCD=12,
∴EC2=12,
∴EC=4 ,
∴BC+CD=BC+BE=EC=4.
变式训练
【变式1-1】.如图,正方形ABCD的对角线AC与BD相交于点O,E,F分别是AB,BC上的点,连接EF.若AE=4,CF=3,OE⊥OF,求EF的长.
解:∵四边形ABCD是正方形,
∴OB=OC,∠BOC=∠EOF=90°,∠ABO=∠ACB=45°,
∴∠EOB=∠FOC,
在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF.BE=CF=3,
∵AB=BC,
∴BF=AE=4,
在Rt△BEF中,BF=4,BE=3,
∴EF=5.
【变式1-2】.如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,作EF⊥BE,垂足为E,直线EF交线段DC于点F,则=_________
解:如图,连接BF,取BF的中点O,连接OE,OC.
∵四边形ABCD是矩形,EF⊥BE,
∴四边形EFCB对角互补,
∴B,C,F,E四点共圆,
∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5,
∵OB=OF,
∴OE=OB=OF=OC,
∴B,C,F,E四点在以O为圆心的圆上,
∴∠EBF=∠ECF,
∴tan∠EBF=tan∠ACD,
∴==,
【例2】.如图,四边形ABCD中,∠ABC=∠ADC=90°,BD平分∠ABC,∠DCB=60°,AB+BC=4,则AC的长是 .
解:设点O是AC的中点,
以O为圆心,OA为半径作圆O,
∵∠ABC=∠ADC=90°,
∴由圆周角定理可知:点D与B在圆O上,
∵BD平分∠ABC,
∴AD=CD,
∴∠DCA=45°,
∴∠ACB=∠DCB﹣∠DCA=15°,
连接OB,过点E作BE⊥AC于点E,
∴由圆周角定理可知:∠AOB=2∠ACB=30°,
∴OB=2BE,
∴AC=2OB=4BE,
设AB=x,
∴BC=4﹣x,
∵AB•BC=BE•AC,
∴4BE2=x(4﹣x),
∴AC2=16BE2=4x(4﹣x),
由勾股定理可知:AC2=x2+(4﹣x)2,
∴4x(4﹣x)=x2+(4﹣x)2,
解得:x=2±,
当x=2+时,
∴BC=4﹣x=2﹣,
∴AC==,
当x=2﹣时,
BC=4﹣x=2+时,
∴AC==,
故答案为:.
变式训练
【变式2-1】.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点在x轴上,对角线AC,BD交于点M,OM=,则点C的坐标为 (6,4) .
解:过点C作CE⊥x轴于点E,过点M作MF⊥x轴于点F,连接EM,
∴∠MFO=∠CEO=∠AOB=90°,AO∥MF∥CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,AM=CM,
∴∠OAB=∠EBC,OF=EF,
∴MF是梯形AOEC的中位线,
∴MF=(AO+EC),
∵MF⊥OE,
∴MO=ME.
∵在△AOB和△BEC中,
,
∴△AOB≌△BEC(AAS),
∴OB=CE,AO=BE.
∴MF=(BE+OB),
又∵OF=FE,
∴△MOE是直角三角形,
∵MO=ME,
∴△MOE是等腰直角三角形,
∴OE==6,
∵A(0,2),
∴OA=2,
∴BE=2,
∴OB=CE=4.
∴C(6,4).
故答案为:(6,4).
【变式2-2】.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= 3 .
解:如图作PQ⊥AB于Q,PR⊥BC于R.
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,
∴==2,
∴PQ=2PR=2BQ,
∵PQ∥BC,
∴AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴2x+3x=3,
∴x=,
∴AP=5x=3.
故答案为3.
【变式2-3】.如图,正方形ABCD,点P是对角线AC上一点,连接BP,过P作PQ⊥BP,PQ交CD于Q,连接BQ交AC于G,若AP=,Q为CD中点,则下列结论:
①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形ABCD的面积是16;
其中正确结论是_________
解:
∵四边形ABCD是正方形,
∴∠BCQ=90°,
∵PQ⊥PB,
∴∠BPQ=90°,
∴∠BPQ+∠BCQ=180°,
∴B、C、Q、P四点共圆,
∴∠PBC=∠PQD,∠BPC=∠BQC,∴①正确;③正确;
过P作PM⊥AD于M,PE⊥AB于E,PF⊥DC于F,则E、P、F三点共线,
∵四边形ABCD是正方形,
∴AB=AD=DC=BC,∠DAC=∠BAC,∠DAB=90°,
∴∠MAE=∠PEA=∠PMA=90°,PM=PE,
∴四边形AMPE是正方形,
∴AM=PM=PE=AE,
∵AP=,
∴在Rt△AEP中,由勾股定理得:AE2+PE2=()2,
解得:AE=AM=PE=PM=1,
∴DF=1,
设AB=BC=CD=AD=a,
则BE=PF=a﹣1,
∵∠BEP=∠PFQ=∠BPQ=90°,
∴∠BPE+∠EBP=90°,∠EPB+∠FPQ=90°,
∴∠EBP=∠FPQ,
在△BEP和△PFQ中
,
∴△BEP≌△PFQ(ASA),
∴PE=FQ=1,BP=PQ,∴②正确;
∴DQ=1+1=2,
∵Q为CD中点,
∴DC=2DQ=4,
∴正方形ABCD的面积是4×4=16,∴④正确;故答案为:①②③④
1.如图,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD= 4 .
解:延长CB到E,使BE=DC,连接AE,AC,
∵∠ABE=∠BAC+∠ACB,
∠D=180°﹣∠DAC﹣∠DCA,
∵∠BAD=90°,∠BCD=90°,
∴∠BAC+∠ACB=90°+90°﹣∠DAC﹣∠DCA=180°﹣∠DAC﹣∠DCA,
∴∠ABE=∠D,
又∵BE=DC,AB=AD,
∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,
∴S△AEC=AE2=,
∵S△AEC=S四边形ABCD=12,
∴=12,
∴EC=4,
∴BC+CD=BC+BE=EC=4.
故答案为:4.
2.如图,在△ABC中,∠ABC=60°,AB=2,BC=8,以AC为腰,点A为顶点作等腰△ACD,且∠DAC=120°,则BD的长为 10 .
解:以A为旋转中心,把△BAC逆时针旋转120°,得到△EAD,连接BE,作AP⊥BE于P,
则∠BAE=120°,AB=AE,
∴∠ABE=∠AEB=30°,
∴BP=AB•cs∠ABP=3,∠DEA=∠ABC=60°,
∴∠DEB=30°+60°=90°,
∴BE=2BP=6,
在Rt△BED中,BD==10,
故答案为:10.
3.如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:
∵∠BAC+∠CAD=∠DAD′+∠CAD,
即∠BAD=∠CAD′,
在△BAD与△CAD′中,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD′,∠DAD′=90°,
由勾股定理得DD′==3,∠D′DA+∠ADC=90°,
由勾股定理得CD′==,
∴BD=CD′=.
故答案为:.
4.四边形ABCD被对角线BD分为等腰直角△ABD和直角△CBD,其中∠A和∠C都是直角,另一条对角线AC的长度为2,求四边形ABCD的面积.
解:将△ABC绕点A旋转90°,使B与D重合,C到C′点,
则有∠CDC′=∠ADC+∠ADC′=∠ADC+∠ABC=180°,
所以C、D、C′在同一直线上,
又因为AC=AC′,
所以△ACC′是等腰直角三角形,
在△ABC和△ADC′中
∴△ABC≌△ADC′(SAS),
∴四边形ABCD的面积等于等腰直角三角形ACC′的面积,
所以S四边形ABCD=S△ACC′=×2×2=2.
5.如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正方形OMNP绕O点旋转,证明:无论正方形OMNP旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值.
解:当OP∥AD或OP经过C点,重叠部分的面积显然为正方形的面积的,
即25,当OP在如图位置时,过O分别作CD,BC的垂线垂足分别为E、F,
如图在Rt△OEG与Rt△OFH中,∠EOG=∠HOF,OE=OF=5,
∴△OEG≌△OFH,
∴S四边形OHCG=S四边形OECF=25,即两个正方形重叠部分的面积为25.
6.基本模型
在任意四边形中,出现一组对角互补,则为对角互补模型.
解题思路:
1.过互补角的顶点作旋转构造全等或相似;
2过互补角的顶点作双垂线构造全等或相似.
问题:
如图,在四边形ABCD中,∠ABC=∠ADC=90°,BD平分∠ABC.
结论:①AD=CD;②AB+BC=BD;③S四边形ABCD=BD2
请证明【基本模型】中的结论.
求证:①AD=CD;②AB+BC=BD;③S四边形ABCD=BD2.
①证明:如图,
过点D作DF⊥BC于点F,DE⊥BA交BA的延长线于点E,
∵BD平分∠ABC,
∴DE=DF,
∵∠ABC=∠ADC=90°,∠DAB+∠ABC+∠C+∠ADC=360°,
∴∠DAB+∠C=180°,
∵∠DAB+∠DAE=180°,
∴∠C=∠DAE,
∴△EAD≌△FCD(AAS),
∴AD=CD;
②证明:如图,
以D为中心将△DAB逆时针旋转90°得到△DCE,
由旋转的性质可得,∠A=∠DCE,∠BDE=90°,DB=DE,AB=CE,
∵∠A+∠BCD=180°,
∴∠DCE+∠BCD=180°,
∴点B,C,E在同一直线上,
∴BE=BC+CE,
∵AB=CE,
∴BE=BC+AB,
∵∠BDE=90°,
∴BE2=DB2+DE2=2BD2,
∴BE=BD,
∴BC+AB=BD;
③证明:如②图,
由旋转的性质可得:△DAB≌△DCE,
∴S四边形ABCD=S△DBE,
∵DB=DE,∠DBE=90°,
∴,
∴.
7.如图1,∠AOB=90°,OC平分∠AOB,以C为顶点作∠DCE=90°,交OA于点D,OB于点E.
(1)求证:CD=CE;
(2)图1中,若OC=3,求OD+OE的长;
(3)如图2,∠AOB=120°,OC平分∠AOB,以C为顶点作∠DCE=60°,交OA于点D,OB于点E.若OC=3,求四边形OECD的面积.
(1)证明:如图1,过点C作CG⊥OA于G,CH⊥OB于H,
∵OC平分∠AOB,
∴CG=CH
∵∠AOB=90°,∠DCE=90°,
∴∠CDO+∠CEO=180°,
∵∠CDG+∠CDO=180°,
∴∠CDG=∠CEO,
在△CDG与△CEH中
,
∴△CDG≌△CEH(AAS),
∴CD=CE;
(2)解:由(1)得△CDG≌△CEH,
∴DG=HE,
由题易得△OCG与△OCH是全等的等腰直角三角形,且OG=OH,
∴OD+OE=OD+OH+HE=OG+OH=2OH,
设OH=CH=x,在Rt△OCH中,由勾股定理,得:
OH2+CH2=OC2
∴x2+x2=32
∴(舍负)
∴OH=
∴OD+OE=2OH=;
(3)解:如图,过点C作CG⊥OA于G,CH⊥OB于H,
∵OC平分∠AOB,
∴CG=CH,
∵∠A0B=120°,∠DCE=60°,
∴∠CDO+∠CEO=180°,
∵∠CDG+∠CDO=180°,
∴∠CDG=∠CEO,
在△CDG与△CEH中
,
∴△CDG≌△CEH(AAS),
∴DG=HE,
由题易得△OCG与△OCH是全等的直角三角形,且OG=OH,
∴OD+OE=OD+OH+HE=OG+OH=2OH,
∴S四边形OECD=S四边形OHCG=2S△OCG
在Rt△OCH中,有∠COH=60°,OC=3,
∴OH=,CH=
∴,
∴S四边形OECD=2S△OCG=.
8.感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= a (用含a的代数式表示)
探究:
证明:如图②中,DE⊥AB于E,DF⊥AC于F,
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DC=DB.
应用:解:如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
,
∴△ADF≌△ADE(HL),
∴AF=AE,
∴AB﹣AC=(AE+BE)﹣(AF﹣CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=45°,BD=a,
∴BE=a,
∴AB﹣AC=a.
故答案为a.
9.问题提出:
(1)如图1,已知线段AB=2,AC=4,连接BC,则三角形ABC面积最大为 4 ;
问题探究:
(2)如图2,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,若CD+BC=10,求四边形ABCD的面积;
问题解决:
(3)在四边形ABCD中,AB=AD,∠BAD+∠BCD=180°,AC=8,求四边形ABCD面积的最大值.
解:(1)如图1,作BG⊥AC于点G,
∵S△ABC=AC•BG,AC=4,
∴S△ABC=×4BG=2BG,
∴当BG最大时,S△ABC的值最大,
∵BG≤AB,AB=2,
∴BG≤2,
∴BG的最大值为2,
∴当BG=2时,S△ABC最大=4,
∴三角形ABC面积最大为4,
故答案为:4.
(2)如图2,连接BD,
∵CD+BC=10,
∴(CD+BC)2=100,
∴CD2+BC2+2CD•BC=100,
∵∠BAD=∠BCD=90°,AB=AD,
∴CD2+BC2=AB2+AD2=BD2,
∴CD2+BC2=2AD2,
∴2AD2+2CD•BC=100,
∴AD2+CD•BC=25,
∵S△ABD=AD2,S△CBD=CD•BC,
∴S四边形ABCD=S△ABD+S△CBD=AD2+CD•BC=25,
∴四边形ABCD的面积为25.
(3)如图3,作AE⊥BC于点E,AF⊥CD交CD的延长线于点F,
∵∠BAD+∠BCD=180°,
∴∠B+∠ADC=180°,
∴∠ADF+∠ADC=180°,
∴∠B=∠ADF,
∵∠AEB=∠F=90°,AB=AD,
∴△ABE≌△ADF(AAS),
∴AE=AF,CE=CF,S△ABE=S△ADF,
∵∠AEC=∠F=90°,AC=AC,
∴Rt△ACE≌Rt△ACF(HL),
∴S△ACE=S△ACF,
∴S四边形ABCD=S△ABE+S四边形AECD=S△ADF+S四边形AECD=S△ACE+S△ACF=2S△ACE,
设AE=m,CE=n,则S四边形ABCD=2S△ACE=2×AE•CE=mn,
∵AE2+CE2=AC2,AC=8,
∴m2+n2=64,
由(m﹣n)2≥0得mn≤(m2+n2),
∴mn≤32,
∴S四边形ABCD≤32,
∴S四边形ABCD最大=32,
∴四边形ABCD面积的最大值是32.
10.定义:有一组对角互补的四边形叫做互补四边形.
(1)概念理解:
①在互补四边形ABCD中,∠A与∠C是一组对角,若∠B:∠C:∠D=2:3:4,则∠A= 90 °;
②如图1,在△ABC中,点D,E分别在边AB,BC上,且BE•BC=AB•BD,求证:四边形ADEC是互补四边形.
(2)探究发现:如图2,在等腰△ABE中,AE=BE,点C,D分别在边BE,AE上,AD=BC,四边形CEDH是互补四边形,求证:∠ABD=∠BAC=∠E.
(1)①解:∵四边形ABCD是互补四边形,∠A与∠C是一组对角,
∴∠C=180°﹣∠A,
∵∠B:∠C:∠D=2:3:4,
∴∠B=,∠D=,
∵∠A+∠B+∠C+∠D=360°,
∴+(180°﹣∠A)+=360°,
∴∠A=90°,
故答案为:90;
②证明:∵BE•BC=AB•BD,
∴,
又∵∠B=∠B,
∴△BDE∽△BCA,
∴∠BED=∠A,
∴∠A+∠CED=∠BED+∠CED=180°,
∴四边形ADEC是互补四边形;
(2)证明:∵AE=BE,AD=BC,
∴ED=EC,
在△EAC和△EBD中,
,
∴△EAC≌△EBD(SAS),
∴∠EBD=∠EAC,
∵AE=BE,
∴∠EAB=∠EBA,
∴∠ABD=∠BAC,
∵四边形CEDH是互补四边形,
∴∠E+∠DHC=180°,
∵∠AHB=∠DHC,
∴∠E+∠AHB=180°,
∴∠ABD+∠BAC=∠E,
∴∠ABD=∠BAC=∠E.
11.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系;
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是 PB=PQ ;
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
解:(1)结论:PB=PQ,
理由:过P作PF⊥BC,PE⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠QPF+∠QPE=90°,
∴∠BPF=∠QPE,
在△PEQ和△PFB中,
,
∴Rt△PQE≌Rt△PBF,
∴PB=PQ;
故答案为PB=PQ.
(2)PB=PQ,
证明:过P作PE⊥BC,PF⊥CD,
∵P,C为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
12.【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等边△AMN,连接CN.求证:BM=CN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论BM=CN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,AB=6,AC=4,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连接CN.试探究BM与CN的数量关系,并说明理由.
解:
(1)证明:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中
∴△ABM≌△ACN(SAS),
∴BM=CN;
(2)成立,理由如下:
∵△ABC和△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠CAM=∠CAM+∠MAN,
∴∠BAM=∠CAN,
在△ABM和△ACN中
∴△ABM≌△ACN(SAS),
∴BM=CN;
(3)=.
理由如下:
∵AB=BC,AM=MN,
∴=,
∵∠AMN=∠ABC,
∴△ABC∽△AMN,
∴=,即=,
∵∠AMN=∠ABC,
∴∠BAC=∠MAN,
∴∠BAM+∠MAC=∠MAC+∠CAN,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴===.
13.定义:对角互补且有一组邻边相等的四边形称为奇异四边形.
(1)概念理解:在平行四边形、菱形、矩形、正方形中,你认为属于奇异四边形的有 正方形 ;
(2)性质探究:
①如图1,四边形ABCD是奇异四边形,AB=AD,求证:CA平分∠BCD;
②如图2,四边形ABCD是奇异四边形,AB=AD,∠BCD=2α,试说明:csα=;
(3)性质应用:
如图3,四边形ABCD是奇异四边形,四条边中仅有BC=CD,且四边形ABCD的周长为6+2,∠BAC=45°,AC=3,求奇异四边形ABCD的面积.
解:(1)根据奇异四边形的定义可知:正方形是奇异四边形,
故答案为正方形.
(2)①过点A作AM⊥CB于M,AN⊥CD于N.
∵∠ABC+∠D=180°,∠ABM+∠ABC=180°,
∴∠ABM=∠D,
∵∠AMB=∠AND=90°,AB=AD,
∴△AMB≌△AND,
∴AM=AN,∵AM⊥CB于M,AN⊥CD于N,
∴CA平分∠BCD.
②由①可知:∠ACD=∠BCD=α,
∵CN=CD﹣DN=CD﹣BM=CD﹣(CM﹣BC)=CD﹣(CN﹣BC),
∴CN=,
在Rt△ACN中,csα==.
(3)如图3中,
由(2)可知:cs45°=,
∴AD+AB=2AC×=6,
∵四边形ABCD的周长为6+2,
∴BC=CD=,
∵∠BAC=∠DAC=45°,
∴∠DAB=90°,
∵四边形是奇异四边形,
∴∠BCD=90°,
∵AD+AB=6,
∴(AD+AB)2=AD2+2AD•AB+AB2=36,
∵AD2+AB2=BD2=BC2+CD2=20,
∴AD•AB=8,
∴S四边形ABCD=S△ADB+S△BDC=•AD•AB+•CD•BC=9.
14.已知:在四边形ABCD中,∠A+∠C=180°,DB平分∠ADC.
(1)求证:AB=BC;
(2)如图2,若∠ADB=60°,试判断△ABC的形状,并说明理由;
(3)如图3,在(2)得条件下,在AB上取一点E,BC上取一点F,连接CE、AF交于点M,连接EF,若∠CMF=60°,AD=EF=7,CD=8(CF>BF),求AE的长.
解:(1)如图,过点B作BF⊥DC于点F,过点B作BE⊥DA,交DA延长线于点E,
则∠BEA=∠BFC=90°,
∵DB平分∠ADC,
∴BE=BF,
又∵∠BAD+∠C=∠BAD+∠BAE=180°,
∴∠C=∠BAE,
在△BEA和△BFC中,
∵,
∴△BEA≌△BFC(AAS),
∴AB=CB;
(2)如图2,连接AC,
∵∠BDA=60°,DB平分∠ADC,
∴∠ADC=2∠ADB=120°,
∵∠BAD+∠C=180°,
∴∠ABC=180°﹣∠ADC=60°,
又AB=BC,
∴△ABC是等边三角形;
(3)如图3,作FG⊥AB于G,EH⊥AF于H,CN⊥AD交AD的延长线于N.
在Rt△CDN中,∵∠CDN=60°,CD=8,
∴∠DCN=30°,
∴DN=CD=4,CN=4,
∴AC===13,
∵AB=BC,∠B=60°,
∴∠ABC是等边三角形,
∴AC=CB=AB=13,∠CAB=60°,
∵∠CMF=∠ACM+∠MAC=60°,
∠MAE+∠MAC=60°,
∴∠ACE=∠BAF,
∵∠CAE=∠B,
∴△ACE≌△BAF(ASA),
∴AE=BF,设AE=BF=x,
则BE=13﹣x,BG=x,EG=13﹣x,FG=x,
在Rt△EFG中,72=(13﹣x)2+(x)2,
解得x=5或x=8,
当x=8时,AE=BF=8,
∵AB=BC=13,
∴CF=BE=5,
此时CF<BF,不符合题意,舍去;
∴AE=BF=5.
15.在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=AB.
(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
解:(1)如图1中,
∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴∠B=∠C=60°,BC=AC=AB=4,
∵点D是线段BC的中点,
∴BD=DC=BC=2,
∵DF⊥AC,即∠CFD=90°,
∴∠CDF=30°,
又∵∠EDF=120°,
∴∠EDB=30°,
∴∠BED=90°
∴BE=BD=1.
(2)如图2中,过点D作DM⊥AB于M,作DN⊥AC于N.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD=AB.
(3)结论不成立.结论:BE﹣CF=AB.
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD=AB.
16.如图,已知∠DCE与∠AOB,OC平分∠AOB.
(1)如图1,∠DCE与∠AOB的两边分别相交于点D、E,∠AOB=∠DCE=90°,试判断线段CD与CE的数量关系,并说明理由.
以下是小宇同学给出如下正确的解法:
解:CD=CE.
理由如下:如图1,过点C作CF⊥OC,交OB于点F,则∠OCF=90°,…
请根据小宇同学的证明思路,写出该证明的剩余部分.
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
(3)若∠AOB=120°,∠DCE=60°.
①如图3,∠DCE与∠AOB的两边分别相交于点D、E时,(1)中的结论成立吗?为什么?
线段OD、OE、OC有什么数量关系?说明理由.
②如图4,∠DCE的一边与AO的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段OD、OE、OC有什么数量关系;如图5,∠DCE的一边与BO的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段OD、OE、OC有什么数量关系.
解:(1)∵OC平分∠AOB,
∴∠AOC=∠BOC=45°,且∠OCF=90°,
∴∠OFC=45°=∠BOC,
∴OC=FC,
∵∠DCE=∠OCF=90°,
∴∠DCO=∠ECF,且CO=CF,∠AOC=∠CFE=45°,
∴△CDO≌△CEF(ASA)
∴CD=CE
(2)如图2,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N,
∴∠CMD=∠CNE=90°,
又∵OC平分∠AOB,
∴CM=CN,
在四边形ODCE中,∠AOB+∠DCE+∠CDO+∠CEO=360°,
又∵∠AOB=∠DCE=90°,
∴∠CDO+∠CEO=180°,
又∵∠CDO+∠CDM=180°,
∴∠CEO=∠CDM,且∠CMD=∠CNE,CM=CN,
∴△CMD≌△CNE(AAS),
∴CD=CE.
(3)①(1)中的结论仍成立.OE+OD=OC.
理由如下:
如图3,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N,
∴∠CMD=∠CNE=90°,
又∵OC平分∠AOB,
∴CM=CN,∠AOC=∠BOC=60°,
在四边形ODCE中,∠AOB+∠DCE+∠CDO+∠CEO=360°,
又∵∠AOB+∠DCE=60°+120°=180°,
∴∠CDO+∠CEO=180°,
又∵∠CEO+∠CEN=180°,
∴∠CDO=∠CEN,且CM=CN,∠CMD=∠CNE,
∴△CMD≌△CNE(AAS),
∴CD=CE,DM=EN.
∴OE+OD=OE+OM+DM=OE+OM+EN=ON+OM.
∵∠AOC=60°,CM⊥AO,
∴∠MCO=30°,
∴,同理可得ON=OC,
∴.
②在图4中,(1)中的结论成立,OE﹣OD=OC,
如图4,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N,
∴∠CMD=∠CNE=90°,
又∵OC平分∠AOB,
∴CM=CN,∠AOC=∠BOC=60°,
∵∠COE+∠CEO+∠DCE+∠OCD=180°,
∴∠OCD+∠CEO=60°,
∵∠AOC=∠CDO+∠OCD=60°,
∴∠CDO=∠CEN,且CM=CN,∠CMD=∠CNE,
∴△CMD≌△CNE(AAS),
∴CD=CE,DM=EN.
∴OE﹣OD=ON+NE﹣(MD﹣OM)=ON+OM.
∵∠AOC=60°,CM⊥AO,
∴∠MCO=30°,
∴,同理可得ON=OC,
∴OE﹣OD=ON+OM=OC;
在图5中,(1)中的结论成立,OD﹣OE=OC,
如图5,过点C作CM⊥OA,CN⊥OB,垂足分别为M,N,
∴∠CMD=∠CNE=90°,
又∵OC平分∠AOB,
∴CM=CN,∠AOC=∠BOC=60°,
∵∠COA+∠CDO+∠DCE+∠OCE=180°,
∴∠OCE+∠CDO=60°,
∵∠NOC=∠CEO+∠OCE=60°,
∴∠CDO=∠CEO,且CM=CN,∠CMD=∠CNE,
∴△CMD≌△CNE(AAS),
∴CD=CE,DM=EN.
∴OD﹣OE=DM+OM﹣(EN﹣ON)=ON+OM.
∵∠AOC=60°,CM⊥AO,
∴∠MCO=30°,
∴,同理可得ON=OC,
∴OD﹣OE=ON+OM=OC;
17.在⊙O中,弦CD平分圆周角∠ACB,连接AB,过点D作DE∥AB交CB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若tan∠CAB=,且B是CE的中点,⊙O的直径是,求DE的长.
(3)P是弦AB下方圆上的一个动点,连接AP和BP,过点D作DH⊥BP于点H,请探究点P在运动的过程中,
的比值是否改变,若改变,请说明理由;若不变,请直接写出比值.
证明:(1)如图1,连接OD交AB于点F,连接OA,OB,AD,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴=,
∴∠AOD=∠BOD,
∵OA=OB,
∴OD⊥AB,
∵AB∥DE,
∴OD⊥DE,
∴DE是⊙O的切线.
解:(2)如图2,连接OC,OD,OE,过点O作OF⊥BC于点F,
∴∠BOC=2∠BAC,
∵OB=OC,OF⊥BC,
∴∠COF=∠∠COB=∠CAB,
∴tan∠COF==tan∠CAB=,
设CF=x,OF=3x,
∵⊙O的直径是,
∴OC=,
∵OC2=OF2+CF2,
∴()2=(3x)2+x2,
解得:x=,
∴CF=,OF=,
∴BC=1,
∵B是CE的中点,
∴BE=BC=1,
∴EF=,
∵OE2=OF2+EF2,
∴OE2=()2+()2=,
∵OD2+DE2=OE2,
∴DE===.
(3)解法一:如图3,延长BP至Q使得PQ=AP,连接AQ,OC,连接OB,BD,连接OD交AB于点K,连接HK,
∵A,P,B,C四点共圆,
∴∠APQ=∠ACB,
∵AP=PQ,
∴∠Q=∠QAP,
∴∠Q=90°﹣∠ACB,
∵DE是⊙O的切线,
∴OD⊥DE,
∵DE∥AB,
∴OD⊥AB,
∴K是AB的中点,
∵DH⊥BH,
∴∠BHD=90°,
∵∠BKD=90°,
∴B,K,H,D四点共圆,
∴∠BHK=∠ODB,
∵∠BOD=∠ACB,OB=OD,
∴∠ODB=90°﹣∠ACB,
∴∠ODB=∠Q,
∴∠BHK=∠Q,
∴AQ∥HK,
∴==,
∵BQ=BP+QP,QP=AP,
∴BQ=BP+AP,
∴=.
解法二:如图4,在BP上截取BM=AP,连接DM,BD,DP,AD,
∵弦CD平分圆周角∠ACB,
∴AD=BD,
∵=,
∴∠PAD=∠PBD=∠MBD,
∴△APD≌△BMD(SAS),
∴DP=DM,AP=BM,
∵DH⊥BP,
∴DH为△PDM的中线,
∴HP=HM,
∴BP=BM+PM=BM+2HM,
∵BH=BM+HM,
∴==.
解法三:如图:连接DA,DB,DP,CD,将△APD沿PD翻折得到△A'PD,
∵∠APD+∠ACD=180°,=,
∴∠BPD=∠ACD,
∴∠BPD+∠APD=180°,
由翻折得△APD≌△A'PD,
∴∠A'PD=∠APD,AD=A'D,
∴∠A'PD+∠BPD=180°,
∴A',P,B三点共线,
∵=,
∴AD=BD,
∴A'D=BD,
又∵DH⊥A'B,
∴A'H=HB=A'B,
∴AP+PH=AP+PB,
∴比值不变,恒为.
18.(1)探究:如图1,在△ABC和△ADE都是等边三角形,点D在边BC上.
①求∠DCE的度数;
②直接写出线段CD,CE,AC之间的数量关系;
(2)应用:如图2,在四边形ABCD中,AB=BC,∠ABC=60°,P是四边形ABCD内一点,且∠APC=120°,求证:PA+PC+PD≥BD;
(3)拓展;如图3,在平面直角坐标系中,点A的坐标为(﹣4,0),点B是y轴上一个动点,以AB为边在AB的下方作等边△ABC,求OC的最小值.
解:(1)①∵△ABC和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
∴∠DCE=∠ACB+∠ACE=120°;
②线段AC、CD、CE之间的数量关系为:AC=CD+CE;
理由是:由①得:△BAD≌△CAE,
∴BD=CE,
∵AC=BC=BD+CD,
∴AC=CD+CE;
(2)如图2,把线段AP绕点A逆时针旋转60度,到AQ.连接AC、PQ,
∴AP=AQ,△APQ为正三角形,
∴∠QAP=60°,QP=AP,
又∵∠APC=120°,
∴∠APC+∠APQ=180°,则C,P,Q在同一条直线上.
∵AB=BC,∠ABC=60°,
∴△ABC为正三角形,
∴∠BAC=60°,AB=AC,
∴∠ABC+∠PAC=∠QAP+∠PAC,
即∠QAC=∠PAB,
∴△ABP≌△ACQ(SAS),
∴PB=QC=PA+PC,
在△PDB中,PB+PD≥BD,即PA+PC+PD≥BD;
(3)如图3,以OA为对称轴作等边△ADE,连接EC,并延长EC交x轴于点F.
在△AEC与△ADB中,,
∴△AEC≌△ADB(SAS),
∴∠AEC=∠ADB=120°,
∴∠OEF=60°,
∴OF=OA=4,
∴点C在直线EF上运动,
当OC⊥EF时,OC最小,
∴OC=OF=2
则OC的最小值为2.
19.有一组邻边相等且对角互补的四边形叫做等邻边互补四边形.
(1)如图1,在等邻边互补四边形ABCD中,AD=CD,且AD∥BC,BC=2AD,求∠B的度数;
(2)如图2,四边形ABCD内接于⊙O,连接DO交AC于点E(不与点O重合),若E是AC的中点,求证:四边形ABCD是等邻边互补四边形;
(3)在(2)的条件下,延长DO交BC于点F,交⊙O于点G,若=,tan∠ABC=,AC=12,求FG的长;
(4)如图3,四边形ABCD内接于⊙O,AB=BC,BD为⊙O的直径,连接AO并延长交BC于点E,交⊙O于点F,连接FC,设tan∠BAF=x,=y,求y与x之间的函数关系式.
(1)解:如图1中,作AH∥CD交BC于H.
∵AD∥BC,AH∥CD,
∴四边形AHCD是平行四边形,
∴AH=CD,AD=BC,
∵AB=CD,AB=AD,BC=2AD,
∴AB=BH=AH,
∴△ABH是等边三角形,
∴∠B=60°.
(2)证明:如图2中,连接CD.
∵ABCD是⊙O的内接四边形,
∴∠B+∠ADC=180°,
∵AE=EC,
∴OD⊥AC,
∴DA=DC,
∴四边形ABCD是等邻边互补四边形.
(3)解:如图2﹣1中,连接OA,OC,AG,CG,作FM⊥CG于M,FN⊥AG于N.
∵AE=EC=6,
∴OD⊥AC,=,
∴∠AOE=∠COE,GA=GC,
∵∠AOC=2∠ABC,
∴∠AOE=∠ABC,
∴tan∠AOE=tan∠ABC==,
∴OE=,OA==,
∴GD=2OA=,DE=OD﹣OE=,
∴AD==,
∴GA=GC==10,
∵=,
∴∠ACB=∠BCG,
∵∠AGF=∠CGF,
∴点F是△AGC的内心,
∴FM=FN=FE,设FM=FN=FE=d,
∵S△ACG=(AC+AG+GC)•d=•AC•EG,
∴d=3,
∴EF=3,
∴GF=EG﹣EF=8﹣3=5.
(4)解:如图3中,连接AC,作AM⊥BC于M,FN⊥BC于N,设AC交BD于K.
∵BD是直径,
∴∠BAD=∠BCD=90°,
∵BA=BC,BD=BD,
∴Rt△ABD≌Rt△CBD(HL),
∴∠ABD=∠CBD,
∵OA=OB,
∴∠BAF=∠ABD=∠CBD,设∠BAF=α,则∠BCF=∠BAF=α,
∵BA=BC,∠DBA=∠DBC,
∴BD⊥AC,
∠BKC=90°,
∴∠ACM+∠CBD=90°,
∵AM⊥BC,
∴∠ACM+∠CAM=90°,
∴∠CAM=∠CBD=α,
∵AM⊥BC,FN⊥BC,
∴AM∥FN,
∴y====•tanα=•x,
设OK=m,AK=n,OB=OA=r,则CF=2m,AC=2n,
在Rt△AOK中,m2+n2=r2,
tan∠ABK=tanα=x==,
∴r=,
∴m2+n2=()2,
整理得:=,
∴y=•x==﹣x2+x,
∴y=﹣x2+(x>0).
模型35 垂美四边形模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型35 垂美四边形模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型35垂美四边形模型原卷版docx、模型35垂美四边形模型解析版docx等2份试卷配套教学资源,其中试卷共49页, 欢迎下载使用。
模型45 折叠变换模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型45 折叠变换模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型45折叠变换模型原卷版docx、模型45折叠变换模型解析版docx等2份试卷配套教学资源,其中试卷共65页, 欢迎下载使用。
模型37 四边形对角互补模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用): 这是一份模型37 四边形对角互补模型(讲+练)-备战2023年中考数学解题大招复习讲义(全国通用),文件包含模型37四边形对角互补模型原卷版docx、模型37四边形对角互补模型解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。












