
所属成套资源:中考数学二轮重难点复习讲义(2份打包,原卷版+解析版)
中考数学二轮重难点复习讲义模型07 将军饮马模型(2份打包,原卷版+解析版)
展开这是一份中考数学二轮重难点复习讲义模型07 将军饮马模型(2份打包,原卷版+解析版),文件包含中考数学二轮重难点复习讲义模型07将军饮马模型原卷版doc、中考数学二轮重难点复习讲义模型07将军饮马模型解析版doc等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
一、两条线段和的最小值。
基本图形解析:
(一)、已知两个定点:
1、在一条直线m上,求一点P,使PA+PB最小;
(1)点A、B在直线m两侧:
(2)点A、B在直线同侧:
A、A’ 是关于直线m的对称点。
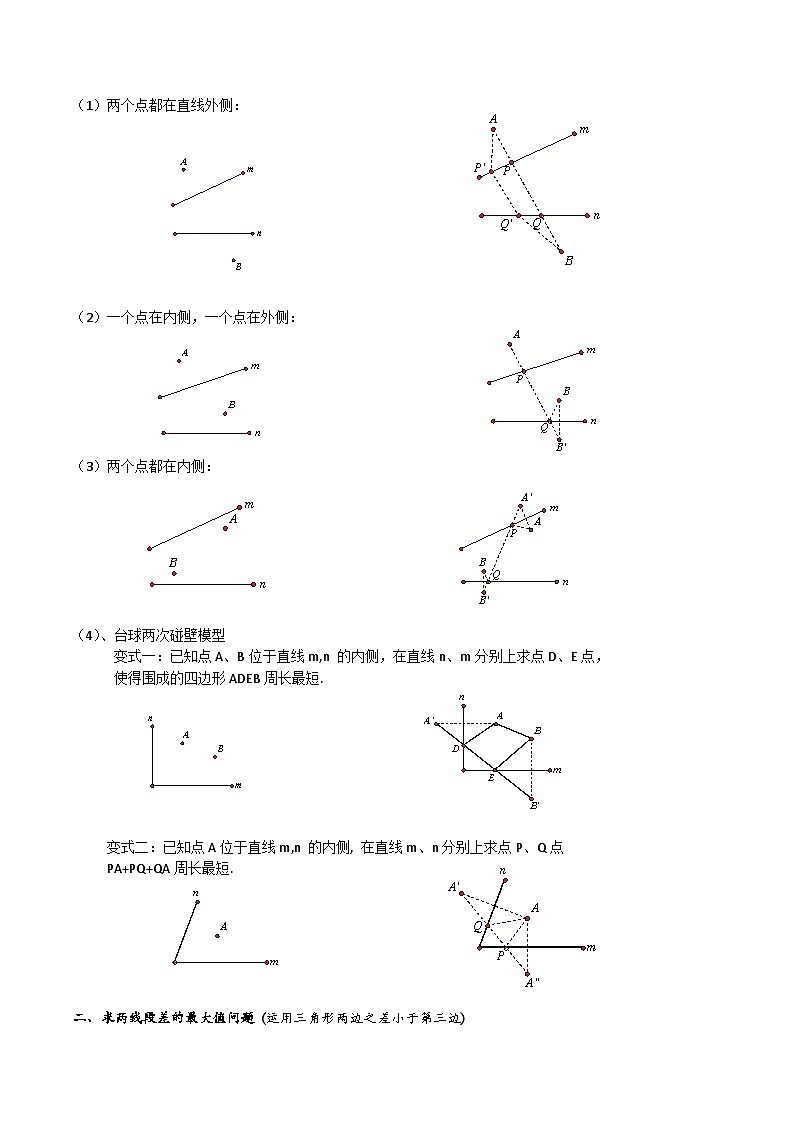
2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。
(1)两个点都在直线外侧:
(2)一个点在内侧,一个点在外侧:
(3)两个点都在内侧:
(4)、台球两次碰壁模型
变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,
使得围成的四边形ADEB周长最短.
变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别上求点P、Q点
PA+PQ+QA周长最短.
二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)
基本图形解析:
1、在一条直线m上,求一点P,使PA与PB的差最大;
(1)点A、B在直线m同侧:
解:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A—P’B<AB,
而PA—PB=AB此时最大,因此点P为所求的点。
(2)点A、B在直线m异侧:
解:过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’,PA-PB最大值为AB’
例题精讲
考点一、两定一动模型
【例1】.如图,在△ABC中,AB的垂直平分线DE交BC于点D,垂足为E,M为DE上任意一点,BA=3,AC=4,BC=6,则△AMC周长的最小值为( )
A.7B.6C.9D.10
解:如图所示,连接BM,
∵DE是AB的垂直平分线,
∴AM=BM,
∴AM+CM=BM+CM,
当B,M,C在同一直线上时,AM+CM的最小值为BC的长,
又∵AC=4,BC=6,
∴△AMC周长的最小值=6+4=10,故选:D.
变式训练
【变式1-1】.如图,Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是( )
A.2B.C.D.4
解:如图,连接BE,则BE就是PA+PE的最小值,
∵Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,
∴CE=2cm,
∴BE==2,
∴PA+PE的最小值是2.
故选:C.
【变式1-2】.如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为 .
解:设△ABP中AB边上的高是h.
∵S△PAB=S矩形ABCD,
∴AB•h=AB•AD,
∴h=AD=2,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=5,AE=2+2=4,
∴BE===,
即PA+PB的最小值为.
故答案为:.
【变式1-3】.如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(5,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为 .
解:作N关于OA的对称点N',连接N'M交OA于P,
则此时,PM+PN最小,
∵OA垂直平分NN',
∴ON=ON',∠N'ON=2∠AON=60°,
∴△NON'是等边三角形,
∵点M是ON的中点,
∴N'M⊥ON,
∵点N(5,0),∴ON=5,
∵点M是ON的中点,∴,
∴,∴.
故答案为:.
考点二、一定两动模型
【例2】.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,AD平分∠CAB交BC于D点,E、F分别是AD,AC上的动点,则CE+EF的最小值为________.
解:在AB上取一点G,使AG=AF,
∵∠CAD=∠BAD,AE=AE,
∴△AEF≌△AEG(SAS),
∴FE=EG,
∴CE+EF=CE+EG,
则最小值时CG垂直AB时,CG的长度,
CG=.
变式训练
【变式2-1】.如图,在Rt△ABC中,∠A=90°,∠B=60°,BC=4,若E是BC上的动点,F是AC上的动点,则AE+EF的最小值为 3 .
解:∵∠A=90°,∠B=60°,
∴∠C=30°,
作A关于BC的对称点D,交BC于H,过D作DF⊥AC于F,交BC于E,
则此时AE+EF的值最小,且AE+EF的最小值=DF,
连接CD,
则△ACD是等边三角形,
∵S△ADC=AC•DF=AD•CH,
∵AD=AC,∴DF=CH,
∵∠BAC=90°,∠ACB=30°,
∴AB=BC=2,
同理BH=AB=1,
∴CH=BC﹣B=3,∴DF=CH=3,
∴AE+EF的最小值为3,
故答案为:3.
【变式2-2】.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是 2 .
解:作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=16,
∴P′D′=2,
即DQ+PQ的最小值为2,
故答案为:2.
【变式2-3】.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 100° .
解:如图,作点A关于BC的对称点A′,关于CD的对称点A″,
连接A′A″与BC、CD的交点即为所求的点M、N,
∵∠BAD=130°,∠B=∠D=90°,
∴∠A′+∠A″=180°﹣∠130°=50°,
由轴对称的性质得:∠A′=∠A′AM,∠A″=∠A″AN,
∴∠AMN+∠ANM=2(∠A′+∠A″)=2×50°=100°.
故答案为:100°.
考点三、线段差最大值模型
【例3】.如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点N,交AB于点M,AB=12cm,△BMC的周长是20cm,若点P在直线MN上,则PA﹣PB的最大值为_______.
解:∵MN垂直平分AC,
∴MA=MC,
又∵C△BMC=BM+MC+BC=20cm,BM+MA=AB=12cm,
∴BC=20﹣12=8(cm),
在MN上取点P,
∵MN垂直平分AC
连接PA、PB、PC
∴PA=PC
∴PA﹣PB=PC﹣PB
在△PBC中PC﹣PB<BC
当P、B、C共线时,即P运动到与P'重合时,(PC﹣PB)有最大值,此时PC﹣PB=BC=8cm.
变式训练
【变式3-1】.如图,已知点A的坐标为(0,1),点B的坐标为(,﹣2),点P在直线y=﹣x上运动,当|PA﹣PB|最大时点P的坐标为_________.
解:作A关于直线y=﹣x对称点C,易得C的坐标为(﹣1,0);连接BC,可得直线BC的方程为y=﹣x﹣;
求BC与直线y=﹣x的交点,可得交点坐标为(4,﹣4);
此时|PA﹣PB|=|PC﹣PB|=BC取得最大值,其他BCP不共线的情况,根据三角形三边的关系可得|PC﹣PB|<BC;
【变式3-2】.如图,两点A、B在直线MN外的同侧,A到MN的距离AC=16,B到MN的距离BD=10,CD=8,点P在直线MN上运动,则|PA﹣PB|的最大值等于 10 .
解:延长AB交MN于点P′,
∵P′A﹣P′B=AB,AB>|PA﹣PB|,
∴当点P运动到P′点时,|PA﹣PB|最大,
∵BD=10,CD=8,AC=16,
过点B作BE⊥AC,则BE=CD=8,AE=AC﹣BD=16﹣10=6,
∴AB===10,
∴|PA﹣PB|的最大值等于10,
故答案为:10.
【变式3-3】.如图,在菱形ABCD中,对角线AC=6,BD=8,点E为AB边的中点,点P为对角线BD上一动点,连接PC,PE,求|PC﹣PE|的最大值.
解:由菱形性质可知,C点关于BD的对称点A,连接AP,则AP=CP,
在△APE中,
|PE﹣PA|<EA,
则当点P、E、A三点共线时,|PE﹣PA|取最大值,最大值为AE.
∴|PC﹣PE|的最大值为AE.
∵菱形ABCD中,对角线AC=6,BD=8,
∴OA=3,OB=4, ∴AB=5,
∵点E为AB边的中点 ∴AE=2.5,
∴|PC﹣PE|的最大值为2.5.
模型四、造桥选址模型(即动线段类型)
【例4】.如图,在矩形ABCD中,AB=5,BC=4,E、F分别是AD、BC的中点,点P、Q在EF上.且满足PQ=2,则四边形APQB周长的最小值为 12 .
解:∵AB=5,PQ=2,
∴四边形APQB的周长为AP+PQ+BQ+AB=AP+BQ+7,
则要使四边形APQB的周长最小,只要AP+BQ最小即可.
在AB边上截取AM=PQ,
∵点F是BC的中点,
∴点B关于EF的对称点为点C,
连接CM,交EF于点Q,
则CM即为AP+BQ的最小值.
在Rt△BCM中,MB=AB﹣AM=5﹣2=3,BC=4,
∴CM==5, ∴四边形APQB的周长最小值为5+7=12. 故答案为:12.
变式训练
【变式4-1】.如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点A、C在坐标轴上,点D的坐标为(6,4),E为CD的中点,点P、Q为BC边上两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标应为 (,0) .
解:点A向右平移2个单位到M,点E关于BC的对称点F,连接MF,交BC于Q,
此时MQ+EQ最小,
∵PQ=2,DE=CE=2,AE=,
∴要使四边形APQE的周长最小,只要AP+EQ最小就行,
即AP+EQ=MQ+EQ,过M作MN⊥BC于N,
设CQ=x,则NQ=6﹣2﹣x=4﹣x,
∵△MNQ∽△FCQ,
∴
∵MN=AB=4,CF=CE=2,CQ=x,QN=4﹣x,
∴,
解得:x=,
∴BP=6﹣2﹣=, 故点P的坐标为:(,0). 故答案为:(,0).
【变式4-2】.如图,正方形ABCD的边长为3,E、F是对角线BD上的两个动点,且EF=,连接CE、CF,则△CEF周长的最小值为 .
解:如图所示,连接AE,AC,以AE,EF为邻边作平行四边形AEFG,
则AE=FG,EF=AG=,∠GAD=∠ADF=45°=∠DAC,
∴∠GAC=90°,
∵AB=CB,∠ABE=∠CBE,BE=BE,
∴△ABE≌△CBE(SAS),
∴CE=AE=GF,
∴CE+CF=GF+CF,
∴当G,F,C在同一直线上时,CF+FG的最小值等于CG的长,
此时,Rt△ACG中,CG===2,
∴CF+FG的最小值等于2,
又∵EF=,
∴△CEF周长的最小值为,
故答案为:.
【变式4-3】.在直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A,B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点,线段EF在边OA上移动,保持EF=2,当四边形CDEF的周长最小时,求点E,F的坐标.
解:如图,作点D关于x轴的对称点D′,在CB边上截取CG=2,
连接D′G与x轴交于点E,在EA上截EF=2,
∵GC∥EF,GC=EF,
∴四边形GEFC为平行四边形,有GE=CF,
又DC、EF的长为定值,
∴此时得到的点E、F使四边形CDEF的周长最小,
∵OE∥BC,
∴Rt△D′OE∽Rt△D′BG,有=,
∴OE====,
∴OF=OE+EF=2=,
∴点E的坐标为( ,0),点F的坐标为( ,0).
实战演练
1.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A.B.4C.5D.
解:作点Q关于AD的对称点Q′,连接PQ′,如图2所示.
∵AD平分∠BAC,
∴点Q′在直线AB上,PQ=PQ′,
∴PC+PQ=PC+PQ′,
∴当CQ′⊥AB,点P为CQ′与AD的交点时,PC+PQ′取得最小值,最小值为CQ′.
在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10,
∴AC•BC=AB•CQ′,即×6×8=×10•CQ′,
∴CQ′=,
∴PC+PQ的最小值为.
故选:D.
2.如图,正方形ABEF的面积为4,△BCE是等边三角形,点C在正方形ABEF外,在对角线BF上有一点P,使PC+PE最小,则这个最小值的平方为( )
A.B.C.12D.
解:连接AC,AE,过C作CG⊥AB,
∵正方形ABEF,
∴AE⊥BF,OA=OE,
即可得:E关于BF的对称点是A,连接AC交BF于P,则此时EP+CP的值最小,
EP+CP=AC,
∵正方形ABEF的面积为4,△BCE是等边三角形,
∴AB=BE=2,BE=BC=2,
在Rt△BCG中,∠CBG=90°﹣60°=30°,BC=2,
∴CG=1,BG=,
∴AC=,
∴AC2=8+4,
即这个最小值的平方为8+4,
故选:B.
3.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A.B.C.D.2
解:法一:
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,),
∴AB=,OA=3,∠B=60°,由勾股定理得:OB=2,
由三角形面积公式得:×OA×AB=×OB×AM,
∴AM=,
∴AD=2×=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=AD=,由勾股定理得:DN=,
∵C(,0),
∴CN=3﹣﹣=1,
在Rt△DNC中,由勾股定理得:DC==,
即PA+PC的最小值是,
法二:
如图,作点C关于OB的对称点D,连接AD,过点D作DM⊥OA于M.
∵AB=,OA=3
∴∠AOB=30°,
∴∠DOC=2∠AOB=60°
∵OC=OD
∴△OCD是等边三角形
∴DM=CD•sin60°=,OM=CM=CD•cs60°=
∴AM=OA﹣OM=3﹣=
∴AD==
即PA+PC的最小值为
故选:B.
4.如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM﹣PN的最大值为( )
A.2B.3C.D.
解:如图所示,以BD为对称轴作N的对称点N',连接MN′并延长交BD于P,连NP,
根据轴对称性质可知,PN=PN',
∴PM﹣PN=PM﹣PN'≤MN',
当P,M,N'三点共线时,取“=”,
∵正方形边长为8,
∴AC=AB=8,
∵O为AC中点,
∴AO=OC=4,
∵N为OA中点,
∴ON=2,
∴ON'=CN'=2,
∴AN'=6,
∵BM=6,
∴CM=AB﹣BM=8﹣6=2,
∴==,
∴PM∥AB∥CD,∠CMN'=90°,
∵∠N'CM=45°,
∴△N'CM为等腰直角三角形,
∴CM=MN'=2,
即PM﹣PN的最大值为2, 故选:A.
5.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是( )
A.0B.4C.6D.8
解:如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H
∵点E,F将对角线AC三等分,且AC=12,
∴EC=8,FC=4=AE,
∵点M与点F关于BC对称
∴CF=CM=4,∠ACB=∠BCM=45°
∴∠ACM=90°
∴EM==4
则在线段BC存在点H到点E和点F的距离之和最小为4<9
在点H右侧,当点P与点C重合时,则PE+PF=12
∴点P在CH上时,4<PE+PF≤12
在点H左侧,当点P与点B重合时,BF==2
∵AB=BC,AE=CF,∠BAE=∠BCF
∴△ABE≌△CBF(SAS)
∴BE=BF=2
∴PE+PF=4
∴点P在BH上时,4<PE+PF≤4
∴在线段BC上点H的左右两边各有一个点P使PE+PF=9,
同理在线段AB,AD,CD上都存在两个点使PE+PF=9.
即共有8个点P满足PE+PF=9,
故选:D.
6.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,当|BC﹣AC|最大时,点C的坐标是 (0,6) .
解:∵A(1,4),B(3,0),
∴直线AB的解析式为y=﹣2x+6,
∵|BC﹣AC|≤AB,
∴当A、B、C三点共线时,|BC﹣AC|的值最大,
此时C(0,6)
故答案为(0,6)
7.如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使三角形AMN周长最小时,则∠MAN的度数为 80° .
解:延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD分别交于点M、N.
∵∠ABC=∠ADC=90°,
∴A、A′关于BC对称,A、A″关于CD对称,
此时△AMN的周长最小,
∵BA=BA′,MB⊥AB,
∴MA=MA′,同理:NA=NA″,
∴∠A′=∠MAB,∠A″=∠NAD,
∵∠AMN=∠A′+∠MAB=2∠A′,∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A′+∠A″),
∵∠BAD=130°,
∴∠A′+∠A″=180°﹣∠BAD=50°,
∴∠AMN+∠ANM=2×50°=100°.
∴∠MAN=180°﹣100°=80°,
故答案为:80°
8.如图,在△ABC中,∠ACB=90°,AC+BC=14,tanB=0.75,点D,E分别是边AB,BC上的动点,则DC+DE的最小值为 .
解:作C关于AB的对称点C',过C'作C'E⊥BC,与AB交于点D,
则DC+DE的最小值即为C'E;
∵∠ACB=90°,AC+BC=14,tanB=0.75,
∴AC=6,BC=8,AB=10,
∴CC'=,
∵∠B=∠C',
∴,
∴C'E=, 故答案为;
9.如图,在▱ABCD中,点M、N分别是AC和BC上的动点,AB=3,BC=6,∠D=60°,在点M、N运动的过程中,BM+MN的最小值为 3 .
解:延长BA到E,使EA=AB,过点E作EN⊥BC于N,交AC于M,连接BM,
在▱ABCD中,∠D=60°,
∴∠ABC=∠D=60°,
∵△ABC中,AB=3,EA=AB,
∴BE=BC=6,△EBC是等边三角形,
∴点E和点B关于AC对称,
∴BM+MN的最小值即为EN的长,
Rt△EBN中,∠BNE=90°,∠ABC=60°,BE=6,
∴BM+MN=EN=BE×sin60°=3.
故答案为:3.
10.如图,在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接 AC,BD,则AC+BD的最小值为 2 .
解:如图,将线段DB向左平移到CE的位置,作点A关于原点的对称点A′,连接CA′,EA′.
则E(﹣2,4),A′(0,﹣2),AC+BD=CA′+CE≥EA′,
EA′==2,
∴AC+BD的最小值为2. 故答案为:2.
11.如图,在等边△ABC中,E是AC边的中点,P是△ABC的中线AD上的动点,且AB=6,则BP﹣PE的最大值是 3 .
解:如图,连接PC,
∵△ABC是等边三角形,AD是中线,
∴AD⊥BC,
∴PC=PB,
∵E是AC边的中点,AB=6,
∴EC=3,
在△PCE中,CP﹣PE<EC,
∴CP﹣PE<3,
∴当P与A重合时,CP﹣PE的值最大为3,
BP﹣PE的最大值是3.故答案为:3.
12.如图,在平面直角坐标系中,点P(4,5),点Q(0,2),当腰长为2的等腰直角三角形ABC在x轴上滑动时,AQ+PC的最小值为 .
解:连接QC、AQ、CO、OP,如右图所示,
∵Q(0,2),△ABC是腰长为2的等腰直角三角形,
∴∠CAO=∠QOA=∠OQC=90°,
∴四边形QOAC是矩形,
∴AQ=OC,
∴AQ+PC=OC+PC,
∵OP<OC+PC,等腰直角三角形ABC在x轴上滑动,
∴当OC+PC等于OP时,取得最小值,
∵点P(4,5),
∴OP==,
∴AQ+PC的最小值是,
故答案为:.
13.如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为 2 .
解:取AB与CD的中点M,N,连接MN,作点B关于MN的对称点E',连接E'C,E'B,
此时CE的长就是GB+GC的最小值;
∵MN∥AD,
∴HM=AE,
∵HB⊥HM,AB=4,∠A=60°,
∴MB=2,∠HMB=60°,
∴HM=1,
∴AE'=2,
∴E点与E'点重合,
∵∠AEB=∠MHB=90°,
∴∠CBE=90°,
在Rt△EBC中,EB=2,BC=4,
∴EC=2,
故答案为2;
14.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值为 4 .
解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故答案为:4.
15.如图抛物线y=x2+2x﹣3与x轴交于A、B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为 .
解:抛物线的对称轴为直线x=﹣1,
当x=0时,y=x2+2x﹣3=﹣3,则C(0,﹣3),
当y=0时,x2+2x﹣3=0,解得x1=﹣3,x2=1,则A(﹣3,0),B(1,0),
∵点D、E、F分别是BC、BP、PC的中点,
∴DE和DF都为△PBC的中位线,
∴DE=PC,DF=PB,
∴DE+DF=(PC+PB),
连接AC交直线x=﹣1于P,如图,
∵PA=PB,
∴PB+PC=PA+PC=AC,
∴此时PB+PC的值最小,其最小值为3,
∴DE+DF的最小值为.
故答案为.
16.如图,正方形ABCD边长为4,DE=1,M,N在BC上,且MN=2.求四边形AMNE周长的最小值.
解:在AD上取一点A′,使得AA′=MN=2,作A′关于BC的对称点A″,连接A″E交BC于N.此时四边形AMNE的周长最短.
由题意AE==,A″E==,
∴四边形AMNE的周长的最小值为2++.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/3/1 9:58:15;用户:初中数学;邮箱:lsjycs@xyh.cm;学号:30145887
17.(1)如图1,OC平分∠AOB,点D是射线OA边上一点,点P、Q分别在射线OC、OB上运动,已知OD=10,∠AOC=30°,则DP+PQ的最小值是 10 ;
(2)如图2,在菱形ABCD中,AB=8,∠DAB=60°,点E是AB边上的动点,点F是对角线AC上的动点,求EF+BF的最小值;
(3)如图3,在矩形ABCD中,AB=8,AD=4,点M是AB上一动点,点N是对角线AC上一动点,请直接写出MN+BN的最小值.
解:(1)当D、P、Q共线且DQ⊥OB时,DP+PQ的值最小,
∴DP+PQ的最小值是5,
故答案为:5;
(2)连接DE、BD,
由菱形的对角线互相垂直平分,可得B、D关于AC对称,则FD=FB,
∴FE+FB=EF+FD=DE,
即DE就是FE+FB的最小值,
∵∠BAD=60°,AD=AB,
∴△ABD是等边三角形,
∵AE=BE,
∴DE⊥AB(等腰三角形三线合一的性质),
在Rt△ADE中,DE===4,
∴EF+BF的最小值=4;
(3)如图3,作点B关于AC的对称点B′,过点B′作B′M⊥AB于M,交AC于N,
连接AB′交DC于P,连接BN,
∵四边形ABCD是矩形,
∴DC∥AB,
∴∠BAC=∠PCA,
∵点B关于AC的对称点是B′,
∴∠PAC=∠BAC,
∴∠PAC=∠PCA,
∴PA=PC.
令PA=x,则PC=x,PD=8﹣x.
在Rt△ADP中,∵PA2=PD2+AD2,
∴x2=(8﹣x)2+42,
∴x=5,
∵cs∠B′AM=cs∠APD,
∴AM:AB′=DP:AP,
∴AM:8=3:5,
∴AM=,
∴B′M===,
∴MN+BN的最小值=.
18.(1)如图①,点P为直线l上一个动点,点A,B是直线l外同侧的两个定点,连接PA,PB,AB.若AB=2,则PA﹣PB的最大值为 2 .
(2)如图②,在四边形ABCD中,AB=AD,∠BAD=90°,对角线AC⊥BD,垂足为点O,OA=2OC,点E为OC中点,点F在AB上,且BF=3AF,点P为BD上一动点,连接PE,PF,若AC=6,求PF﹣PE的最大值.
(3)如图③,在△ABC中,AB=AC=3,∠BAC=150°,点P为平面内一动点,连接PA,PB,PC.若PA=2,求PB﹣PC的最大值.
解:(1)根据三角形三边关系两边之差小于第三边,
∴只有当A、B、P共线时PA﹣PB有最大值为AB=2,
故答案为:2;
(2)如图②,作点E关于BD的对称点E',连接FE'并延长交BD于P',
同理(1)可知,此时F、E、P共线PF﹣PE有最大值为FE',
∵AC=6,OA=2OC,OA+OC=AC,
∴OA=4,OC=2,
∵点E为OC中点,
∴OE=OC=1,
根据对称性得:OE'=OE=1,
∵AB=AD,∠BAD=90°,AC⊥BD,
∴△AOB为等腰直角三角形,
∴AB=AO=4,
∵BF=3AF,AF+BF=AB,
∴AF=,
作FH⊥AC于H,
∵△AOB为等腰直角三角形,
∴∠BAE=45°,
即△AFH也为等腰直角三角形,
∴AH=FH=AF=1,
∴HE'=AO﹣AH﹣OE'=4﹣1﹣1=2,
∴FE'===,
故PF﹣PE的最大值为;
(3)如图③,将△APC绕A点顺时针旋转150°得到△AP'B,则PC=P'B,
∴当点P、P'、B三点共线时,PB﹣PC有最大值为PP',
作PO⊥P'A延长线于O,
∵∠BAC=150°,
∴∠OAP=30°,
∴OP=AP=1,
∴OA===,
∴P'O=2+,
∴P'P====,
∴P'B﹣P'C=,
故PB﹣PC的最大值为.
19.如图所示,抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标;
(2)在抛物线的对称轴上找一点P,使得△ACP的周长最小,请求出点P的坐标;
(3)若点N是第四象限内抛物线上的一个动点,连接BN、CN,求△BCN面积的最大值及此时点N的坐标.
解:(1)抛物线y=x2﹣2x﹣3,当x=0时,y=﹣3,
∴C(0,﹣3),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为M(1,﹣4).
(2)如图1,由(1)得,抛物线的对称轴为直线x=1,
设直线x=1交BC于点D,点P为直线x=1上任意一点,连接AD、PB,
∵AC为定值,
∴当PA+PC的值最小时,△ACP的周长最小,
∵点B与点A关于直线x=1对称,
∴PA=PB,
∴PA+PC=PB+PC,
∵PB+PC≥BC,
∴当点P与点D重合时,PA+PC=PB+PC=BC,
此时PB+PC的值最小,PA+PC的值也最小,
抛物线y=x2﹣2x﹣3,当y=0时,则x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
设直线BC的解析式为y=kx﹣3,则3k﹣3=0,
解得k=1,
∴直线BC的解析式为y=x﹣3,
当x=1时,y=﹣2,
∴P(1,﹣2).
(3)如图2,过点N作NF⊥x轴于点F,交BC于点E,
设点N的坐标为(x,x2﹣2x﹣3),则E(x,x﹣3),
∴EN=(x﹣3)﹣(x2﹣2x﹣3)=﹣x2+3x,
∵S△BCN=S△CEN+S△BEN=EN•OF+EN•BF=OB•EN,
∴S△BCN=×3(﹣x2+3x)=﹣(x﹣)2+,
∴当x=时,S△BCN最大=,此时N(,﹣),
∴△BCN面积的最大值为,N(,﹣).
20.如图,已知直线与y轴交于点A,与x轴交于点D,抛物线与直线交于A、E两点,与x轴交于B、C两点,且线段OA=OB.
(1)求该抛物线的解析式;
(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标;
(3)在抛物线的对称轴上找一点M,使|AM﹣CM|的值最大,求点M的坐标.
(注:抛物线y=ax2+bx+c的对称轴为)
解:(1)∵直线与y轴交于点A,
∴A点坐标为;(0,1),
∵线段OA=OB,
∴B(1,0),
将A(0,1)、B(1,0)坐标代入y=x2+bx+c
得,
解得,
∴抛物线的解析式为y=x2﹣x+1;
(2)设点E的横坐标为m,则它的纵坐标为m2﹣m+1,
即E点的坐标(m,m2﹣m+1),
又∵点E在直线y=x+1上,
∴m2﹣m+1=m+1
解得m1=0(舍去),m2=4,
∴E的坐标为(4,3).
(Ⅰ)当A为直角顶点时,
过A作AP1⊥DE交x轴于P1点,设P1(a,0)易知D点坐标为(﹣2,0),
由Rt△AOD∽Rt△P1OA得=即=,
∴a=,
∴P1(,0).
(Ⅱ)同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,
由Rt△AOD∽Rt△P2ED得,=即=,
∴EP2=,
∴DP2==,
∴a=﹣2=,
P2点坐标为(,0).
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(t,0),
由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,
由=得=,
解得t1=3,t2=1,
∴此时的点P3的坐标为(1,0)或(3,0),
综上所述,满足条件的点P的坐标为(,0)或(1,0)或(3,0)或(,0);
(3)抛物线的对称轴为x=,
∵B、C关于x=对称,
∴MC=MB,
要使|AM﹣MC|最大,即是使|AM﹣MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大.
易知直线AB的解析式为y=﹣x+1
∴由,
得,
∴M(,﹣).
相关试卷
这是一份中考数学二轮重难点复习讲义模型17 阿氏圆最值问题(2份打包,原卷版+解析版),文件包含中考数学二轮重难点复习讲义模型17阿氏圆最值问题原卷版doc、中考数学二轮重难点复习讲义模型17阿氏圆最值问题解析版doc等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
这是一份中考数学常见几何模型全归纳提分精练专题09最值模型-将军饮马(原卷版+解析),共54页。试卷主要包含了求两条线段和的最小值,平移型将军饮马,修桥选址模型, 求多条线段和最小值,求两条线段差最大值等内容,欢迎下载使用。
这是一份2024年中考数学二轮复习 最值模型之将军饮马模型(原卷版+解析版),共30页。












