初中数学北师大版八年级下册3 中心对称图片ppt课件

这是一份初中数学北师大版八年级下册3 中心对称图片ppt课件，共24页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，中心对称，中心对称的性质，中心对称图形，答案B等内容，欢迎下载使用。
中心对称中心对称的性质中心对称图形
1. 定义 如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做它们的对称中心. 这两个图形在旋转前后能重合的对应点叫做关于对称中心的对称点.
特别解读♦中心对称是指两个图形的位置关系，必须涉及两个图形；♦中心对称的两个图形，只有一个对称中心.这个对称中心可能在每个图形的外部，也可能在每个图形的内部或边上.
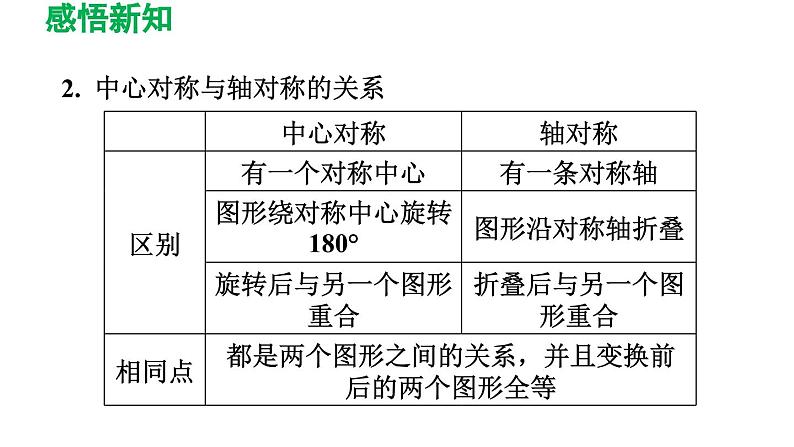
2. 中心对称与轴对称的关系
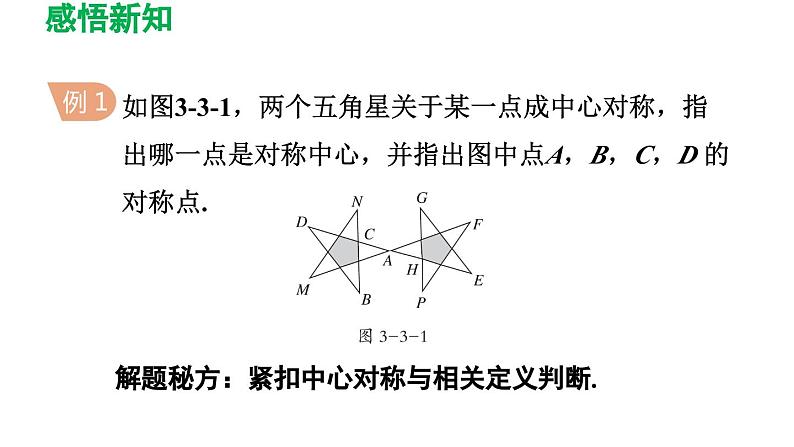
如图3-3-1，两个五角星关于某一点成中心对称，指出哪一点是对称中心，并指出图中点A，B，C，D 的对称点.
解题秘方：紧扣中心对称与相关定义判断.
解：从图中易看出旋转中心为点A，故点A 为对称中心；点A，B，C，D 绕点A 旋转180°后的位置分别在点A，G，H，E 处，故点A，B，C，D 关于点A 的对称点分别是点A，G，H，E.
1-1. 下列四组图形中，右边图形与左边图形成中心对称的有________(填序号).
1. 中心对称的性质(1)成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分；反之，如果两个图形的对应点的连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点中心对称，利用这一性质可以识别中心对称.(2)中心对称的两个图形是全等图形，对应角相等，对应线段平行(或在一条直线上)且相等.
2. 利用中心对称的性质作图的步骤(1)将原图形上的所有关键点与对称中心连接；(2)将以上连线延长找对称点，使得对称点与对称中心的距离和关键点与对称中心的距离相等；(3)将对称点按原图形的形状顺次连接起来，即可得出关于对称中心对称的图形.
特别解读♦由性质可以得到如下结论：1. 对称中心在一对对称点的连线上;2. 对称中心到一对对称点的距离相等.♦全等的图形不一定成中心对称，而成中心对称的两个图形一定是全等的图形.
如图3-3-2，已知四边形ABCD和点O，画四边形A′B′C′D′，使四边形A′B′C′D′与四边形ABCD 关于点O成中心对称．
解题秘方：要作四边形ABCD 关于点O 成中心对称的图形，只要作出点A，B，C，D 关于点O 的对称点，然后顺次连接即可.
解：(1)连接AO 并延长AO 到A′，使OA′= OA，于是得到点A 关于点O 的对称点A′.(2)同样画出点B，C和点D关于点O的对称点B′，C′和D′.(3)连接A′B′，B′C′，C′D′，D′A′，则四边形A′B′C′D′即为所求作的图形．如图3-3-2 所示.
2-1. 如图， 已知△ABC，以点O为对称中心，求作与△ABC 成中心对称的图形.
1. 中心对称图形 把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心.
特别提醒判断中心对称图形的方法：1. 中心对称图形的“三要素”(1) 对称中心；(2) 旋转180°；(3) 与本身重合.2. 常见的中心对称图形线段、平行四边形、长方形、正方形、边数是偶数的正多边形、圆等.
2. 中心对称与中心对称图形的区别和联系
[中考·恩施州] 下列图形中，既是轴对称图形又是中心对称图形的是( )
解题秘方：紧扣中心对称图形和轴对称图形的定义进行识别，掌握轴对称图形和中心对称图形的特征是解题的关键.
解：A. 是轴对称图形, 不是中心对称图形，故本选项不合题意；B. 既是轴对称图形, 又是中心对称图形, 故本选项符合题意；C. 不是轴对称图形, 是中心对称图形，故本选项不合题意；D. 不是轴对称图形, 是中心对称图形, 故本选项不合题意.
3-1. [中考· 山西]为推动世界冰雪运动的发展， 我国于2022 年举办北京冬奥会，在此之前进行了冬奥会会标的征集活动， 以下是部分参选作品，其文字上方的图案既是轴对称图形又是中心对称图形的是( )