2023年河南省郑州市第一中学中考数学二模试题（含答案）

这是一份2023年河南省郑州市第一中学中考数学二模试题（含答案），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列各数中，最大的是（ ）
A． B．0 C． D．
2．（3分）据中国教育报2023年3月14日公布的数据显示，今年高校毕业生达1158万人，比去年增加80余万人，创历史新高，将数据“80万”用科学记数法表示为（ ）
A． B． C． D．
3．（3分）《天净沙·秋思》中的词句意境幽远．如图所示，该图形经过折叠可以围成一个正方体，折好以后，与“小”字相对的字是（ ）
A．流 B．水 C．人 D．家
4．（3分）如图所示，，将一块三角板如图所示放置（直角顶点C在上），若，则的度数为（ ）
A． B． C． D．
5．（3分）下列计算正确的是（ ）
A． B． C． D．
6．（3分）关于x的一元二次方程有实数根，则k可能是（ ）
A． B． C．1 D．
27．（3分）某数学兴趣小组准备了4张卡片，正面依次书写“备”“战”“中”“考”，它们除此之外完全相同，把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片的正面汉字恰能组成“备考”的概率是（ ）
A． B． C． D．
8．（3分）如图所示，在中，，以点B为圆心，长为半径弧，与交于点D，再分别以A、D为同心，大于的长为平径画弧，两弧交于点E、F，作直线，分别交于点P、Q，则的长度为（ ）
A． B． C． D．
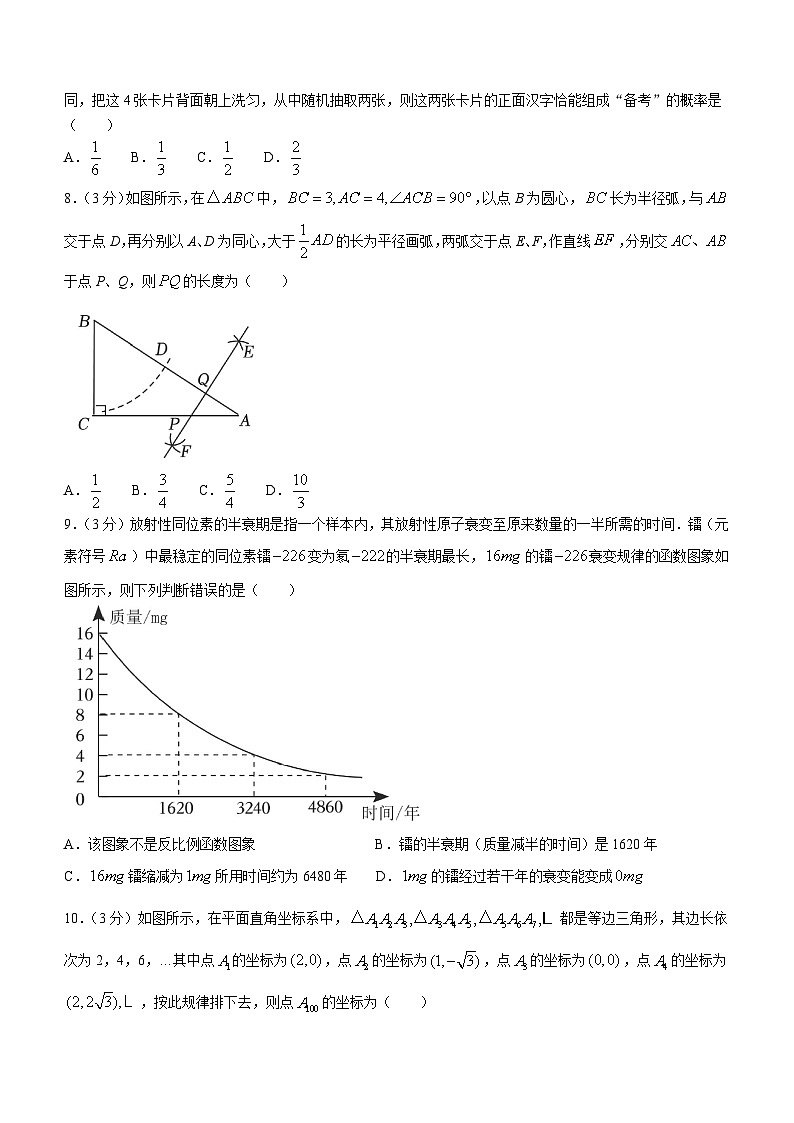
9．（3分）放射性同位素的半衰期是指一个样本内，其放射性原子衰变至原来数量的一半所需的时间．镭（元素符号）中最稳定的同位素镭变为氡的半衰期最长，的镭衰变规律的函数图象如图所示，则下列判断错误的是（ ）
A．该图象不是反比例函数图象 B．镭的半衰期（质量减半的时间）是1620年
C．镭缩减为所用时间约为6480年 D．的镭经过若干年的衰变能变成
10．（3分）如图所示，在平面直角坐标系中，都是等边三角形，其边长依次为2，4，6，…其中点的坐标为，点的坐标为，点的坐标为，点的坐标为，按此规律排下去，则点的坐标为（ ）
A． B． C． D．
二、填空题（每小题3分，共15分）
11．（3分）比较大小：_____________2（填“>”或“<”或“=”）
12．（3分）不等式组的解集是_____________．
13．（3分）甲、乙两名学生5次立定跳远成绩的平均数相同，若甲5次立定跳远成绩的方差为，乙5次立定跳远成绩的方差为，则甲、乙两名学生5次立定跳远成绩比较稳定的是_____________．（选填“甲”或“乙”）
14．（3分）如图所示，扇形中，点C为的中点，点D为的中点，连接交于点P，则阴影部分图形的面积是__________________________（结果保留π）．
15．（3分）如图所示，在中，，点P、O分别为上两点，且，将绕点C在平面内旋转，连接．当时，的长为____________________．
三、解答题（本大题共8个小题，满分75分）
16．（10分）（1）计算：；
（2）化简：．
17．（9分）2022年，教育部正式印发《义务教育课程方案》，将劳动从原来的综合实践活动课程中完全独立出来，并发布《义务教育劳动课程标准（2022年版）》，文中对家务劳动的时间做了细致要求．某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在本校随机调查了25名学生的“劳动时间”，并进行统计，绘制了如下统计表：
根据上述信息，回答下列问题：
（1）此次调查属于_____________调查，样本容量为_____________，个体为____________________；
（2）这25名学生的“劳动时间”的中位数落在_____________组；若要绘制扇形图，C组学生所对圆心角的度数为_____________；
（3）若该校有1400名学生，请估计在该校学生中，“劳动时间”不少于90分钟的人数．
18．（9分）如图所示，一次函数反比例函数的图象在第象限交于点P，且点P的横坐标为2．
（1）求反比例函数的解析式；
（2）在第一象限内是否存在点Q，使得以B、O、P、Q为顶点的四边形为平行四边形，若存在，请求出点Q坐标，若不存在，请说明理由．
19．（9分）大汉雄风（图2）坐落于河南省永城市芒砀山主峰，是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建，是亚洲最大的历史人物雕像，外为塑铜焊接，内是钢架结构，雄浑庄重．如图1所示，小敏在数学实践活动中，利用所学知识对刘邦雕像的高度进行测量，她在与雕像底部平齐的水平线上放置一无人机，且无人机所在的位置D与B的距离为，将无人机从D点垂直上升到C处，测得点A的仰角为，测得点B的俯角为，求刘邦雕像的高度．（结果保留整数．参考数据：）
图1 图2
20．（9分）已知一个零刻度落在点A的量角器（半圆O）的直径为，一等腰直角三角板绕点B旋转．
图1 图2
（1）如图1所示，当等腰直角三角板的斜边交半圆于C点，一直边交半圆于D点，另一直边交半圆于E点，若点C在量角器上的读数为，求此时点E在量角器上的读数：
（2）如图2所示，当点C、D在量角器上的读数满足什么关系时，直角边与半圆O相切于点D？请说明理由．
21．（9分）某校体育社团由于报名人数激增，决定从某体育用品店购买若干足球和篮球，用于日常训练，已知每个篮球的价格比每个足球的价格多30元，用900元购买足球的数量是用720元购买篮球数量的2倍．
（1）求篮球和足球的单价各是多少？
（2）根据学生报名情况，社团需一次性购买篮球和足球共80个，且要求购买足球数量不超过篮球数量的，请你设计一个购买方案使得购买费用最少，最少费用为多少元？
22．（10分）己知二次函数的图象与x轴交于点A、（点A在点B的左侧）两点，与y轴交于点．点P是直线上的一动点．
图1 备用图
（1）求该二次函数的解析式；
（2）过点P作轴，交抛物线于点Q，设的长度为h，点P的横坐标为，若h值随的增大而增大，请确定P的横坐标的取值范围．
23．（10分）【问题发现】如图1所示，将绕点A逆时针旋转得，连接根据条件填空：
图1 图2 图3
①的度数为_____________°;②若，则的值为_____________；
【类比探究】如图2所示，在正方形中，点E在边上，点F在边上，且满足，求正方形的边长；
【拓展延伸】如图3所示，在四边形中，为对角线，且满足，若，请直接写出的值．
2023年河南省郑州一中中考数学二模试卷
参考答案与试题解析
一、选择题（每小题3分，共30分．下列各小题均有四个答案，其中只有一个是正确的．）
1．【解答】解：，
，
，
∴所给的各数中，最大的是．
故选：D．
2．【解答】解：80万．
故选：C．
3．【解答】解：根据“Z”与形法则，可得与“小”字相对的字是”家，
故选：D．
4．【解答】解：过点B作，
，
，
，
，
，
故选：B．
15．【解答】解：A、，故A选项不符合题意；
B、不能合并，故B选项不符合题意；
C、，故C选项不符合题意；
D、，故D选项符合题意．
故选：D．
6．【解答】解：根据题意得，
即，
只有满足，而、1、都不满足．
故选：A．
7．【解答】解：列表如下：
由表知，共有12种等可能结果，其中这两张卡片的正面汉字恰能组成“备考”的有2种结果，所以这两张卡片的正面汉字恰能组成“备考”的概率为，
故选：A．
8．【解答】解：由题意得，，直线为的垂直平分线，
，
，
，
，
，即，
，
故选：B．
9．【解答】解：由图象知，图象过点，该图象不是反比例函数图象，故A不符合题意；每过1620年镭质量减少一半，故B不符合题意；
的镭缩减为需要四次衰变，（年），故C不符合题意；
的镭经过n年的衰变质量为，故D符合题意．
故选：D．
10．【解答】解：观察所给图形，发现x轴上方的点是4的倍数，
，
∴点在x轴上方，
，
，
，
，
，
∴点的坐标为，
同理可知，点的坐标为，
∴点的坐标为．
故选：C．
二、填空题（每小题3分，共15分）
11．【解答】解：，
，
故答案为：>．
12．【解答】解：由得：，
由得：，
则不等式组的解集为，
故答案为：．
13．【解答】解：∵甲、乙两名学生5次立定跳远成绩的平均数相同，甲5次立定跳远成绩的方差为，乙5次立定跳远成绩的方差为，
，
∴甲、乙两名学生5次立定跳远成绩比较稳定的是甲，
故答案为：甲．
14．【解答】
解：连接交于点Q，
∵点C为的中点，
，
，
，
，
是等边三角形
，
∵点D为的中点，
，
，
，
，
．
故答案为：．
15．【解答】解：，
，
，
，
，
∵将绕点C在平面内旋转，点P的对应点为点，
∴点在以点C圆心，为半径的圆上，
当时，存在两种情况，
当点P在线段上时，;
当点P与延长线上时，连接，如图，
过点B作于点H，则，
，
，
综上，的长为2或．
故答案为：2或．
三、解答题（本大题共8个小题，满分75分）
16．【解答】解：（1）原式
；
（2）原式
．
17．【解答】解：（1）此次调查属于抽样调查，样本容量为25，个体为每名学生的劳动时间；故答案为：抽样；25；个体为每名学生的劳动；
（2）把25名学生的“劳动时间”从小到大排列，第13个数位于C组，
所以这25名学生的“劳动时间”的中位数落在C组；
若要绘制扇形图，C组学生所对圆心角的度数为．
故答案为：C;；
（3）（人），
答：估计在该校学生中，“劳动时间”不少于90分钟的人数大约为1064人．
18．【解答】（1）解：与的图象在第一象限交于点P，且点P的横坐标为2，
∴当时，，
，
，
，
∴反比例函数的解析式为；
（2）解：存在，理由如下：
在中，当时，，
，
，
当以B，O，P，Q为顶点的四边形为平行四边形时，分两种情况：
①当为平行四边形的边时，
∵点Q在第一象限，
，
∵点P的坐标为，且，
∴点Q在点P的下方，
∴点Q坐标为；
②当为平行四边形的对角线时，点在点P的上方，可得点的坐标为，
或．
19．【解答】解：如图所示，点C作于点E，
由题意得，，
，
在中，，
，
．
答：刘邦雕像的高度约为．
20．【解答】解：（1）如图1，连接，∵点C在量角器上的读数为，
，
，
，
；
（2）．理由：如图2，连接，
∵直角边与半圆O相切于点D，
，
，
，
，
，
．
图1 图2
21．【解答】解：（1）设足球的单价是x元，则篮球的单价是元，
根据题意，得，
解得，
经检验，是原方程的解，且符合题意，
．
答：篮球的单价是80元，足球的单价是50元；
（2）设学校购买m个篮球，则购买足球个，购买费用为w元，
则，
∵购买足球数量不超过篮球数量的，
，
解得，
，
∴当时，w有最小值，最小值为5800元，
此时，
答：社团购买60个篮球，20个足球费用最少，最少费用为5800元．
22．【解答】解：（1）把分别代入得，
解得，
∴二次函数解析式为;
（2）设直线的解析式为，
把分别代入得，
解得，
∴直线的解析式为，
设，则，
当时，，
，
∴当时，h值随的增大而增大；
当或时，，
当时，，
解得或，
或，
，
∴当时，h值随的增大而增大，
，
综上所述，P的横坐标的取值范围为或．
23．【解答】【问题发现】解：①将绕点A逆时针旋转得，
，
，
故答案为：45；
②是等腰直角三角形，，
，
故答案为：；
【类比探究】解：将绕A逆时针旋转得，如图所示：
绕A逆时针旋转得，
，
，
∴G、D、C共线，
，
，
即，
在与中，
，
，
，
，
设正方形边长为x，则，
在中，，
，
解得：或（舍去），
∴正方形的边长为；
【拓展延伸】解：将绕C逆时针旋转至，连接，如图所示：
，
，
，
，
，
，
，
，
，
，
，
．
组别
“劳动时间”/分钟
频数
A
2
B
4
C
10
D
9
备
战
中
考
备
战备
中备
考备
战
备战
中战
考战
中
备中
战中
考中
考
备考
战考
中考