




沪科版九年级下册24.1.2 中心对称作业ppt课件
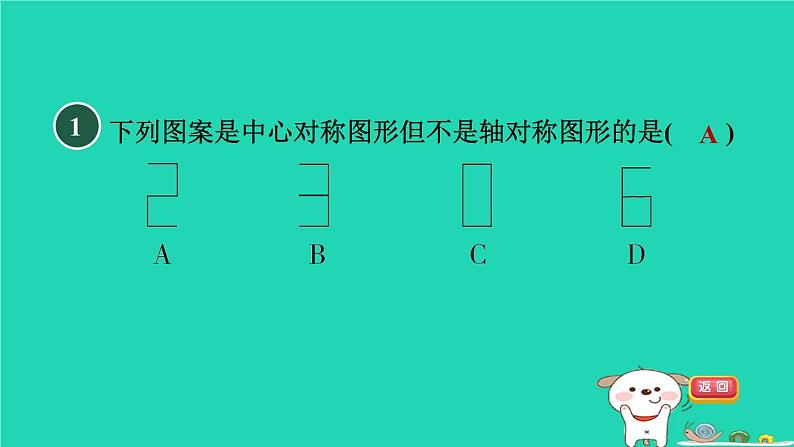
展开下列图案是中心对称图形但不是轴对称图形的是( )
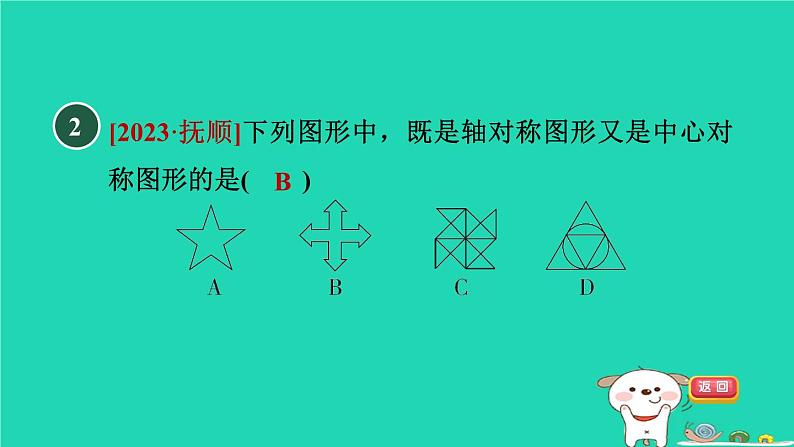
[2023·抚顺]下列图形中,既是轴对称图形又是中心对称图形的是( )
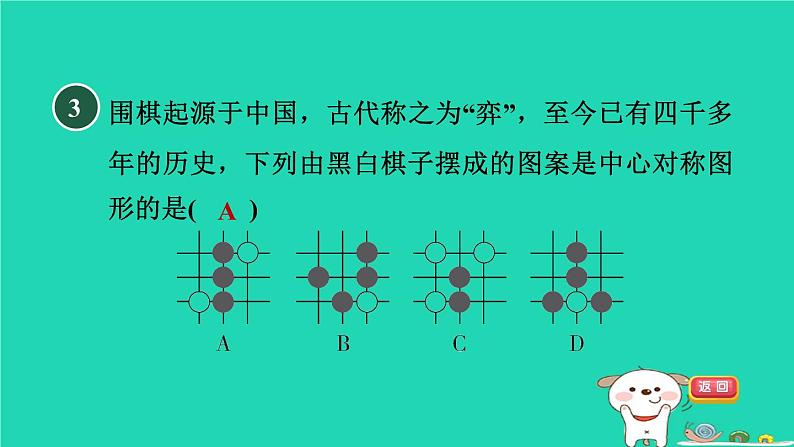
围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是中心对称图形的是( )
如图,△ABC与△CDA关于点O成中心对称,过点O任意作直线EF,分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D分别关于点O成中心对称;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为( )A.2 B.3 C.4 D.5
在Rt△AOC中,∠A=30°,OC=1,∴OA=2OC=2.根据中心对称图形的性质可知OB=OA=2,点A,O,B共线,∴AB=4.
如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,修路的方法有( )A.1种 B.2种 C.4种 D.无数种
∵正方形是中心对称图形,∴过正方形的对称中心作互相垂直的两条直线,则这两条直线把草地分成的四部分面积相等,故选D.
图a和图b中所有的小正方形都全等,将图a的正方形放在图b中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是_______.
当小正方形放在③的位置时,组成的图形是中心对称图形.
下列图案中是旋转对称图形,但不是中心对称图形的是( )
A选项中的图案是旋转对称图形,不是中心对称图形,故本选项符合题意;B,C,D选项中的图案是旋转对称图形,也是中心对称图形,不符合题意.故选A.
注意中心对称图形是旋转对称图形的特例,当旋转对称图形绕某一个定点旋转180°后能与原图形重合时,该图形是中心对称图形.
图①,图②均是4×4的正方形网格,每个小正方形的顶点称为格点,其中点A,B,C均在格点上,请在给定的网格中按要求画四边形.
(1)在图①中,找一格点D,使以点A,B,C,D为顶点的四边形是轴对称图形;
【解】如图①,四边形ABCD即为所求.(答案不唯一)
(2)在图②中,找一格点E,使以点A,B,C,E为顶点的四边形是中心对称图形.
【解】如图②,四边形ABCE即为所求.(答案不唯一)
如图,点O是▱ABCD的对称中心,连接AC,DB,将DB绕点O按顺时针方向旋转,分别交DC,AB于点E,F,连接AE,CF.
(1)求证:△DEO≌△BFO;
【证明】∵四边形ABCD是平行四边形,∴CD∥AB.∴∠EDO=∠FBO.∵点O是▱ABCD的对称中心,∴OD=OB.又∵∠EOD=∠FOB,∴△DEO≌△BFO.
当DB绕点O按顺时针方向旋转45°,即∠DOE=45°时,∠AOE=∠AOD+∠DOE=90°.∴AC⊥EF.由(1)得△DEO≌△BFO.∴OE=OF.又∵点O是▱ABCD的对称中心,∴OA=OC.∴四边形AECF是平行四边形.又∵AC⊥EF,∴四边形AECF是菱形.
知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.(1)如图①,直线m经过平行四边形ABCD对角线的交点O,试判断S四边形AEFB与S四边形DEFC的数量关系;
【解】S四边形AEFB=S四边形DEFC.
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).
【解】如图②③④所示.
数学九年级下册24.1.3 中心对称图形作业ppt课件: 这是一份数学九年级下册<a href="/sx/tb_c102897_t3/?tag_id=26" target="_blank">24.1.3 中心对称图形作业ppt课件</a>,共21页。PPT课件主要包含了解如图所示,①②③等内容,欢迎下载使用。
沪科版九年级下册24.1.1 图形的旋转作业课件ppt: 这是一份沪科版九年级下册<a href="/sx/tb_c102895_t3/?tag_id=26" target="_blank">24.1.1 图形的旋转作业课件ppt</a>,共20页。PPT课件主要包含了点B′,∠A′,OB′等内容,欢迎下载使用。
沪科版九年级下册第24章 圆24.1 旋转24.1.3 中心对称图形作业ppt课件: 这是一份沪科版九年级下册第24章 圆24.1 旋转24.1.3 中心对称图形作业ppt课件,共12页。













