
北师大版七年级数学下册同步精讲精练专题全等三角形模型——手拉手模型与半角模型(原卷版+解析)
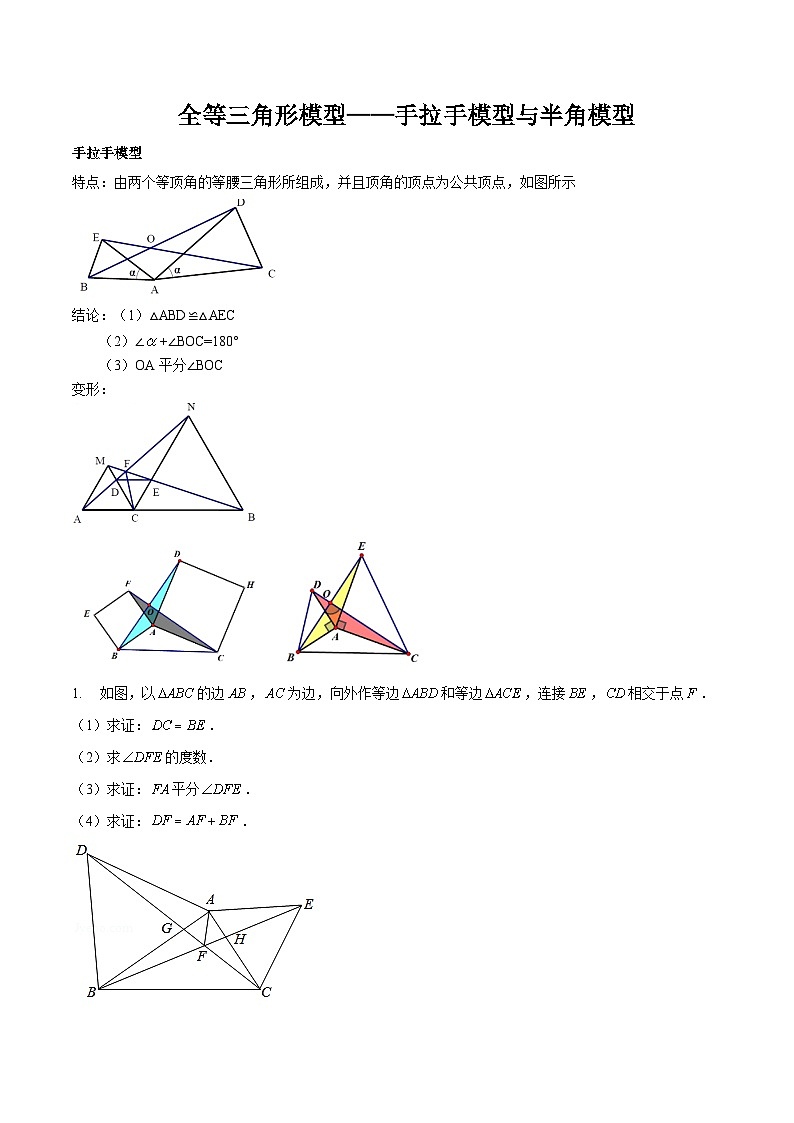
展开特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点,如图所示
结论:(1)△ABD≌△AEC
(2)∠+∠BOC=180°
(3)OA平分∠BOC
变形:
如图,以的边,为边,向外作等边和等边,连接,相交于点.
(1)求证:.
(2)求的度数.
(3)求证:平分.
(4)求证:.
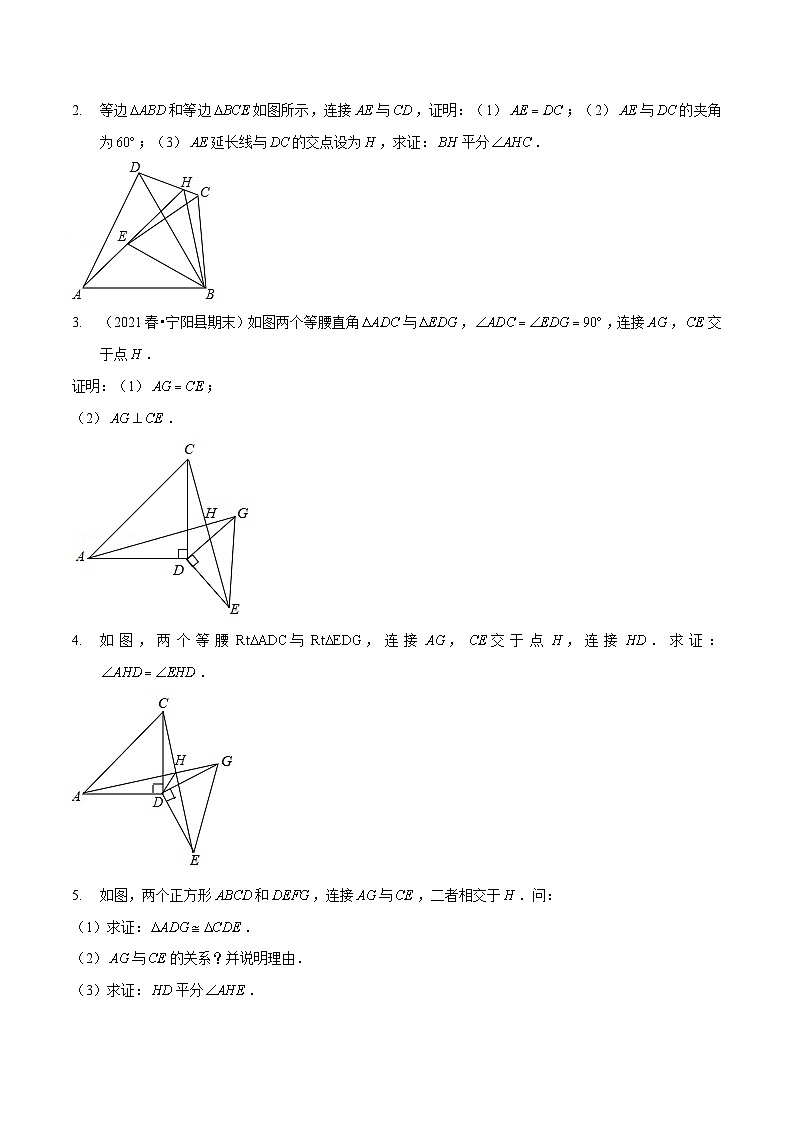
等边和等边如图所示,连接与,证明:(1);(2)与的夹角为;(3)延长线与的交点设为,求证:平分.
(2021春•宁阳县期末)如图两个等腰直角与,,连接,交于点.
证明:(1);
(2).
如图,两个等腰与,连接,交于点,连接.求证:.
如图,两个正方形和,连接与,二者相交于.问:
(1)求证:.
(2)与的关系?并说明理由.
(3)求证:平分.
(2021秋•南岗区校级期中)已知:,,.
(1)如图1,求证:;
(2)如图2,当时,、交于点,连接,求证:;
(3)如图3,在(2)的条件下,过作于,在上取点,连接并延长至,使,连接,若,求的度数.
(2021秋•天河区期末)是等边三角形,点是边上动点,,把沿对折,得到△.
(1)如图1,若,则 .
(2)如图2,点在延长线上,且.
①试探究,,之间是否存在一定数量关系,猜想并说明理由.
②若,,求的长.(用含的式子表示)
半角模型
图形中,往往出现90°套45°的情况,或者120°套60°的情况。还有套的情况。求证的结论一般是线段的和与差。解决的方法是:截长补短构造全等三角形。旋转移位造全等,翻折分割构全等。截长法,补短法。
(2021秋•东坡区期末)如图,是边长为6的等边三角形,,,以点为顶点作一个角,使其两边分别交于点,交于点,连结,则的周长是 .
已知,如图,四边形是正方形,、分别在边、上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法
(1)在图1中,连接,为了证明结论“”,小明将绕点顺时针旋转后解答了这个问题,请按小明的思路写出证明过程;
(2)如图2,当的两边分别与、的延长线交于点、,连接,试探究线段、、之间的数量关系,并证明.
(2020秋•荔湾区期末)如图,在四边形中,,,,分别是边,上的点,且,求证:.
已知:边长为1的正方形中,、分别是、上的点.
(1)若,求证:;
(2)若得周长为2,求的度数.
(2020秋•新建区校级期中)(1)如图(1),在中,是边上的中点,,交于点,交于点,连接.若,探索线段、、之间的数量关系,并加以证明;
(2)如图(2),在四边形中,,,,以为顶点作一个角,角的两边分别交、于、两点,连接,探索线段、、之间的数量关系,并加以证明.
【感知】如图①,点是正方形的边上一点,点是延长线上一点,且,易证,进而证得(不要求证明)
【应用】如图②,在正方形中,点、分别在边、上,且.求证:.
【拓展】如图③,在四边形中,,,,点、分别在边、上,且,若,,则四边形的周长为 .
问题背景:“半角问题”
(1)如图:在四边形中,,,.,分别是,上的点.且.探究图中线段,,之间的数量关系.
小明同学探究此“半角问题”的方法是:延长到点.使.连接,先证明,再证明,可得出结论,他的结论应是 ;(直接写结论,不需证明)
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“,”换为.其它条件不变.如图1,试问线段、、具有怎样的数量关系,并证明.
(3)如图2,在四边形中,,,、分别是边、上的点,且,请直接写出线段、、它们之间的数量关系.(不需要证明)
(4)如图3,在四边形中,,,、分别是边、延长线上的点,且,试问线段、、具有怎样的数量关系,并证明.
全等三角形模型——手拉手模型与半角模型
手拉手模型
特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点,如图所示
结论:(1)△ABD≌△AEC
(2)∠+∠BOC=180°
(3)OA平分∠BOC
变形:
如图,以的边,为边,向外作等边和等边,连接,相交于点.
(1)求证:.
(2)求的度数.
(3)求证:平分.
(4)求证:.
【分析】(1)根据等边三角形的性质和全等三角形的判定和性质得出即可;
(2)根据全等三角形的性质和角的关系得出即可;
(3)过点作于,于,根据三角形面积公式和角平分线的性质解答即可;
(4)在上截取,连接,根据全等三角形的判定和性质解答即可.
【解答】证明:(1)和是等边三角形,
,,,
,
即,
在与中,
,
,
;
(2),
,
,
,
;
(3)过点作于,于,
,
,
,
,
,,
平分;
(4)在上截取,连接,
在与中,
,
,
,,
,
,
,
即,
是等边三角形,
,
.
等边和等边如图所示,连接与,证明:(1);(2)与的夹角为;(3)延长线与的交点设为,求证:平分.
【分析】(1)根据和都是等边三角形,即可得到,进而得出;
(2)根据全等三角形的性质以及三角形内角和定理,即可得到中,,进而得到与的夹角为;
(3)过作于,于,根据全等三角形的面积相等,即可得到,再根据于,于,可得平分.
【解答】证明:(1)和都是等边三角形,
,,,
,
在和中,
,
,
;
(2),
,
又,
,
中,,
即与的夹角为;
(3)如图,过作于,于,
,
,即,
又,
,
又于,于,
平分.
(2021春•宁阳县期末)如图两个等腰直角与,,连接,交于点.
证明:(1);
(2).
【分析】(1)由两个等腰直角与,可得,,,进而得出,然后由即可判定,进而可得结论;
(2)根据全等三角形的性质则可证得,再根据直角三角形的两锐角互余进而证出即可得解.
【解答】解:(1)证明:与是等腰直角三角形,
,,且,
,
即,
在与中,
,
,
;
(2)证明:设与相交于点,由(1)知,,
,
,
,
,
,
,
.
如图,两个等腰与,连接,交于点,连接.求证:.
【分析】由“”可证,可得,,由面积公式可得,由角平分线的判定定理可得结论.
【解答】证明:如图,过点作于,于,
,
,
在和中,
,
,
,,
,
,
又,,
.
如图,两个正方形和,连接与,二者相交于.问:
(1)求证:.
(2)与的关系?并说明理由.
(3)求证:平分.
【分析】(1)由四边形与是正方形,可得,,进而得出,,然后由即可判定;
(2)根据全等三角形的性质则可证得,,进而证出即可;
(3)根据全等三角形的性质和三角形的面积解答即可.
【解答】(1)证明:四边形和四边形是正方形,
,,且,
,
在与中,,
,
(2)解:,,理由如下:
由(1)得:,
,,
,
,
;
(3)证明:过点作于,于,如图:
,
,
,
,
,,
平分.
(2021秋•南岗区校级期中)已知:,,.
(1)如图1,求证:;
(2)如图2,当时,、交于点,连接,求证:;
(3)如图3,在(2)的条件下,过作于,在上取点,连接并延长至,使,连接,若,求的度数.
【分析】(1)证明即可;
(2)作,,截取,证明,可推出,从而可证,进而得证;
(3)作于,作交于,作于,证明,可推出,进而求得结果.
【解答】(1)证明:如图1,
,
,
,
,,
,
;
(2)证明:如图2,
设与交于,作于,于,在上截取,
,
由(1)知:,
,
,
,
,
,
,
,
是等边三角形,
,
,
,
,
即:;
(3)解:如图3,
作于,作交于,作于,
,,
,
,
,
,
,
,
,
,
,
,
由(2)知:,
,
,
,
,
,
,
,
,
,,
,
,
,
.
(2021秋•天河区期末)是等边三角形,点是边上动点,,把沿对折,得到△.
(1)如图1,若,则 .
(2)如图2,点在延长线上,且.
①试探究,,之间是否存在一定数量关系,猜想并说明理由.
②若,,求的长.(用含的式子表示)
【分析】(1)由是等边三角形知,,由,知,,代入值即可;
(2)①连接,在上取一点,使,根据证△,得,再证是等边三角形,即可得出;
②先证,即、、三点在同一直线上,得出,根据证△,得出,即可求出的值.
【解答】解:(1)是等边三角形,
,
,
,
,
,
,
故答案为:;
(2)①,理由如下:
连接,在上取一点,使,
是等边三角形,
,,
,
△,
,,
,
,
是等边三角形,
,,
,
即;
②如下图,
由①知,,
,
由(1)知,,
由折叠知,,
,
,
,
,
点、、在同一直线上,
即,
由折叠知,,,
,
,
,
△,
,
由①知,,
,,
,
,
.
半角模型
图形中,往往出现90°套45°的情况,或者120°套60°的情况。还有套的情况。求证的结论一般是线段的和与差。解决的方法是:截长补短构造全等三角形。旋转移位造全等,翻折分割构全等。截长法,补短法。
(2021秋•东坡区期末)如图,是边长为6的等边三角形,,,以点为顶点作一个角,使其两边分别交于点,交于点,连结,则的周长是 .
【分析】要求的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长至,使,连接,通过证明,及,从而得出,的周长等于的长.
【解答】解:是等腰三角形,且,
,
是边长为4的等边三角形,
,
,
延长至,使,连接,
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
的周长是:.
故答案为:12.
已知,如图,四边形是正方形,、分别在边、上,且,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法
(1)在图1中,连接,为了证明结论“”,小明将绕点顺时针旋转后解答了这个问题,请按小明的思路写出证明过程;
(2)如图2,当的两边分别与、的延长线交于点、,连接,试探究线段、、之间的数量关系,并证明.
【分析】(1)利用旋转的性质,证明即可;
(2)把绕点逆时针旋转到,交于点,证明即可求得.
【解答】(1)证明:由旋转可得,,,
四边形为正方形,
,
,
,
,
,
在和中,
,
,
,
,
;
(2)解:线段、、之间的数量关系是:,证明如下:
把绕点逆时针旋转,使与重合,点与点对应,如图:
同(1)可证得,
,且,
.
(2020秋•荔湾区期末)如图,在四边形中,,,,分别是边,上的点,且,求证:.
【分析】延长至,使,连接,先证,得,,再证,得,进而得出结论.
【解答】证明:延长至,使,连接,如图所示:
,,
,
在与中,
,
,
,,
,
,
,
即,
在与中,
,
,
,
,
.
已知:边长为1的正方形中,、分别是、上的点.
(1)若,求证:;
(2)若得周长为2,求的度数.
【分析】(1)延长到,使,连接,因为,,,所以,则有,,又因为,,所以,故,即;
(2)延长至,使,则,故,进而求证,即可求得.
【解答】(1)证明:延长到,使,连接,
,,,
,
.
,,
,,
,
.
,
,
.
(2)解:如图,延长到,使,连接,
,,,
,
.
,,
,
又,
,
.
(2020秋•新建区校级期中)(1)如图(1),在中,是边上的中点,,交于点,交于点,连接.若,探索线段、、之间的数量关系,并加以证明;
(2)如图(2),在四边形中,,,,以为顶点作一个角,角的两边分别交、于、两点,连接,探索线段、、之间的数量关系,并加以证明.
【分析】(1)如图(1)延长到,使,连接,,根据条件证明,得,,易证垂直平分线段,则,把问题转化到中,由勾股定理可求解;
(2)如图(2),结论:.延长到,使,根据条件证明,则,再证明,从而得.
【解答】证明:(1),
理由如下:如图(1)延长到,使,连接,,
在与中,
,
,
,,,
又,
垂直平分线段,
,
,
,
,
在中,,
;
(2)如图(2),结论:,
理由如下:延长到,使,
,又,
,
在和中,
,
,
,,
,
在和中,
,
,
,
.
【感知】如图①,点是正方形的边上一点,点是延长线上一点,且,易证,进而证得(不要求证明)
【应用】如图②,在正方形中,点、分别在边、上,且.求证:.
【拓展】如图③,在四边形中,,,,点、分别在边、上,且,若,,则四边形的周长为 .
【分析】【应用】如图②中,过点作交延长线于点.先证明,再证明,得到,由此即可证明.
【拓展】如图③中,如图③中,过点作交延长线于点.首先证明,由此即可计算四边形的周长.
【解答】【应用】如图②中,过点作交延长线于点.
四边形为正方形,
,.
,.
,.
.
在和中,
,
.
,.
,,
.
在和中,
,
.
.
,
.
【拓展】如图③中,过点作交延长线于点.
,,
,
,.
.
在和中,
,
.
,.
,,
.
在和中,
,
.
.
,
.
四边形的周长为,
故答案为6.4
问题背景:“半角问题”
(1)如图:在四边形中,,,.,分别是,上的点.且.探究图中线段,,之间的数量关系.
小明同学探究此“半角问题”的方法是:延长到点.使.连接,先证明,再证明,可得出结论,他的结论应是 ;(直接写结论,不需证明)
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“,”换为.其它条件不变.如图1,试问线段、、具有怎样的数量关系,并证明.
(3)如图2,在四边形中,,,、分别是边、上的点,且,请直接写出线段、、它们之间的数量关系.(不需要证明)
(4)如图3,在四边形中,,,、分别是边、延长线上的点,且,试问线段、、具有怎样的数量关系,并证明.
【分析】(1)延长到点.使.连接,即可证明,可得,再证明,可得,即可解题;
(2)如图1,延长到,使,连接,即可证明,可得,再证明,可得,即可解题;
(3)如图2,同理可得:;
(4)如图3,作辅助线,构建,同理证明和.可得新的结论:.
【解答】证明:(1)延长到点.使.连接,
在和中,
,
,
,,
,,
,
,
在和中,
,
,
,
;
故答案为:;
(2)如图1,延长到,使,连接.
在与中,
,
.
,,
.
.
又,
易证.
.
.
(3)(1)中的结论仍然成立.
理由是:如图2,延长到,使,连接.
,,
,
在与中,
,
.
,,
.
.
又,
.
.
.
(4)结论不成立,应当是.
证明:在上截取,使,连接.
,,
.
在与中,
,
.
,.
.
.
,
易证.
.
中考数学常见几何模型全归纳提分精练专题02全等模型-半角模型(原卷版+解析): 这是一份中考数学常见几何模型全归纳提分精练专题02全等模型-半角模型(原卷版+解析),共37页。试卷主要包含了半角模型,5=40,BD=90×0等内容,欢迎下载使用。
最新中考数学难点突破与经典模型精讲练 专题02 全等三角形中的半角模型 (全国通用): 这是一份最新中考数学难点突破与经典模型精讲练 专题02 全等三角形中的半角模型 (全国通用),文件包含专题02全等三角形中的半角模型原卷版docx、专题02全等三角形中的半角模型解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
2024年中考数学几何模型专项复习讲与练 模型12 全等三角形——手拉手模型-原卷版+解析: 这是一份2024年中考数学几何模型专项复习讲与练 模型12 全等三角形——手拉手模型-原卷版+解析,共19页。












