2023-2024学年江苏省连云港市灌云高级中学少年班七年级（上）期中数学试卷（含解析）

这是一份2023-2024学年江苏省连云港市灌云高级中学少年班七年级（上）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.计算1+(−2)的结果是( )
A. −1B. 1C. 3D. −3
2.在下列各数1.3⋅，π，0，227，1.010010001，−3.14，0.262662666…(每两个2之间依次增加一个数6)中，无理数的个数有( )
A. 4个B. 3个C. 2个D. 1个
3.下列各式运用等式的性质变形，正确的是( )
A. 若a=b，则a+c=b−cB. 若ac=bc，则a=b
C. 若ac=bc，则a=bD. 若(m2−1)a=(m2−1)b，则a=b
4.下列运算中，正确的是( )
A. 3a+b=3abB. −3a2−2a2=−5a4
C. −2(x−4)=−2x−4D. −3a2b+2a2b=−a2b
5.2023年歌曲《罗刹海市》席卷全球，据统计截止八月中旬，播放量突破惊人的358亿，数字35800000000用科学记数法表示为( )
A. 358×108B. 3.58×109C. 3.58×1010D. 35.8×109
6.若ab>0，则a|a|+b|b|+ab|ab|的值为( )
A. 3B. −1C. ±1或±3D. 3或−1
7.如图，将−3，−2，−1，0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a，b，c分别表示其中的一个数，则a−b+c的值为( )
A. −5
B. −4
C. 0
D. 5
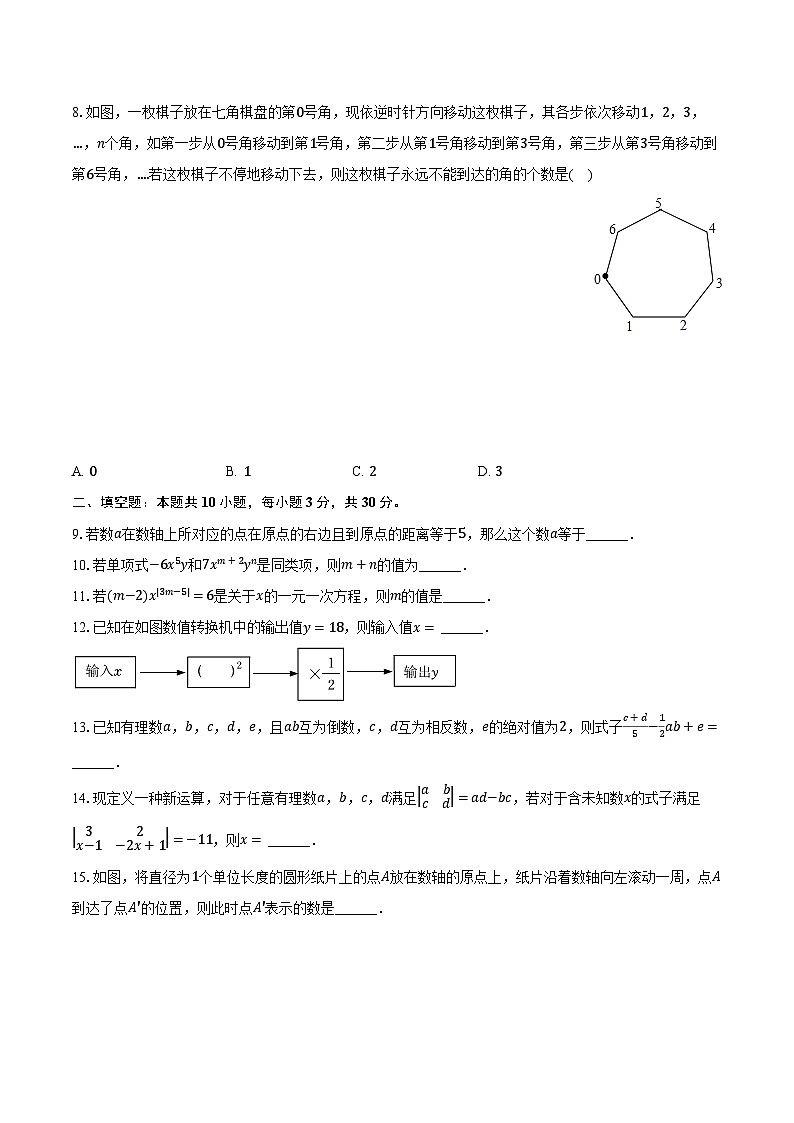
8.如图，一枚棋子放在七角棋盘的第0号角，现依逆时针方向移动这枚棋子，其各步依次移动1，2，3，…，n个角，如第一步从0号角移动到第1号角，第二步从第1号角移动到第3号角，第三步从第3号角移动到第6号角，….若这枚棋子不停地移动下去，则这枚棋子永远不能到达的角的个数是( )
A. 0B. 1C. 2D. 3
二、填空题：本题共10小题，每小题3分，共30分。
9.若数a在数轴上所对应的点在原点的右边且到原点的距离等于5，那么这个数a等于______．
10.若单项式−6x5y和7xm+2yn是同类项，则m+n的值为______．
11.若(m−2)x|3m−5|=6是关于x的一元一次方程，则m的值是______．
12.已知在如图数值转换机中的输出值y=18，则输入值x= ______．
13.已知有理数a，b，c，d，e，且ab互为倒数，c，d互为相反数，e的绝对值为2，则式子c+d5−12ab+e= ______．
14.现定义一种新运算，对于任意有理数a，b，c，d满足abcd=ad−bc，若对于含未知数x的式子满足32x−1−2x+1=−11，则x= ______．
15.如图，将直径为1个单位长度的圆形纸片上的点A放在数轴的原点上，纸片沿着数轴向左滚动一周，点A到达了点A′的位置，则此时点A′表示的数是______．
16.如果a，b为定值，关于x的一次方程kx+2a2−x−bk6=12，无论k为何值时，它的解总是1，则6a+b= ______．
17.若(3x−1)5=a0+a1x+a2x2+a3x3+a4x4+a5x5，则a1+a2+a3+a4+a5= ______．
18.如图，将一个边长为1的正方形纸片分割成7个图形，图形①面积是正方形纸片面积的13，图形②面积是图形①面积的2倍的13，图形③面积是图形②面积的2倍的13，…，图形⑥面积是图形⑤面积的2倍的13，图形⑦面积是图形⑥面积的2倍.计算13+29+427+⋯+2536的值为______．
三、解答题：本题共9小题，共96分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题16分)
计算题：
①(−3)−(−1.5)−(−3)+(+3.5)；
②(−34−59+712)÷(−136)；
③−32×[−32×(−23)2−2]；
④−16−16×[3−(−3)2]−2÷(−12).
20.(本小题8分)
解下列方程：
(1)2(3−x)=−4(x+5)；
(2)2y−14−1=5y−76．
21.(本小题12分)
(1)先化简再求值：2(x2+3y)−(2x2+3y−x)，其中x=1，y=−2．
(2)先化简，再求值：5(a2b−3ab2)−2(a2b−7ab2)，其中a=−1，b=1．
22.(本小题8分)
出租车司机小张某天下午的运营是在一条东西走向的大道上.如果规定向东为正，他这天下午的行程记录如下：(单位：千米)+15，−3，+14，−11，+10，−18，+14．
(1)将最后一名乘客送到目的地时，小张离下午出车点的距离是多少？
(2)若汽车的耗油量为0.06升/千米，油价为7.5元/升，这天下午共需支付多少油钱？
23.(本小题8分)
已知A=5x2−mx+n，B=3x2−2x+1．
(1)若m为最小的正整数，且m+n=0，求A−B；
(2)若A−B的结果中不含一次项和常数项，求m2+n2−2mn的值．
24.(本小题10分)
某中学库存若干套桌椅，准备修理后支援贫困山区学校．现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费．
(1)该中学库存多少套桌椅？
(2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案：a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理．你认为哪种方案省时又省钱？为什么？
25.(本小题8分)
关于x的整式，当x取任意一组相反数m与−m时，若整式的值相等，则该整式叫做“偶整式”；若整式的值互为相反数，则该整式叫做“奇整式”.例如：x2是“偶整式”，x3是“奇整式”．
(1)若整式A是关于x的“奇整式”，当x取1与−1时，对应的整式值分别为A1，A2，则A1+A2= ______；
(2)对于整式x5−x3+x2+x+1，可以看作一个“偶整式”与“奇整式”的和．
①这个“偶整式”是______，“奇整式”是______；
②当x分别取−3，−2，−1，0，1，2，3时，这七个整式的值之和是______．
26.(本小题12分)
将整数1，2，3…2009按下列方式排列成数表，用斜十字框“╳”框出任意的5个数(如下图)，如果用a、b、c、d、m(m处于斜十字中心)表示类似“╳”形框中的5个数．
(1)记S=a+b+c+d+m，若S最小，那么m= ______若S最大，那么m= ______．
(2)用等式表示a，b，c，d，m这5个数之间的关系并说明理由．
(3)若a+b+c+d=240.求m的值．
(4)框出的五个数中，a，b，c，d的和能等于588吗？若能，求出m的值；若不能，请说明理由．
27.(本小题14分)
已知a，b满足(a−4)2+|16−b|=0，a，b分别对应数轴上的A，B两点．
(1)直接写出a= ______，b= ______；
(2)若点P从点A出发，以每秒3个单位长度的速度向数轴正方向运动，求运动时间为多少时，点P到点A的距离是点P到点B的距离的2倍？
(3)数轴上还有一点C对应的数为30.若点P和点Q同时从点A和点B出发，分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动.P点到达C点后，再立刻以同样的速度返回，运动到终点A，点Q达到点C后继续向前运动.求点P和点Q运动多少秒时，P，Q两点之间的距离为4？
答案和解析
1.【答案】A
【解析】解：1+(−2)
=1−2
=−1．
故选：A．
直接利用有理数加减运算法则计算得出答案．
此题主要考查了有理数的加减运算，正确掌握运算法则是解题关键．
2.【答案】C
【解析】解：1.3⋅是循环小数，属于有理数；
0是整数，属于有理数；
227是分数，属于有理数；
1.010010001，−3.14是有限小数，属于有理数；
无理数有π，0.262662666…(每两个2之间依次增加一个数6)，共2个．
故选：C．
根据无理数是无限不循环小数，可得答案．
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．
3.【答案】C
【解析】解：A：只有当c=0时成立，故A不符合题意；
B：当c=0时不成立，故B不符合题意；
C：根据等式的性质，两边都乘以c，两边相等，故C不符合题意；
D：当m=±1时不成立，故D不符合题意；
故选：C．
根据等式的性质判断求解．
本题考查了等式的性质，理解等式的性质是解题的关键．
4.【答案】D
【解析】解：A.3a与b不是同类项，不能合并，此选项错误；
B.−3a2−2a2=−5a2，此选项错误；
C.−2(x−4)=−2x+8，此选项错误；
D.−3a2b+2a2b=−a2b，此选项正确；
故选：D．
根据同类项的定义、合并同类项法则、去括号法则及合并同类项法则逐一计算即可得．
本题主要考查整式的加减，解题的关键是掌握同类项的定义、合并同类项法则、去括号法则及合并同类项法则．
5.【答案】C
【解析】【分析】
本题主要考查科学记数法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．解题关键是正确确定a的值以及n的值．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同，据此进行解答即可．
【解答】
解：358亿=35800000000=3.58×1010．
6.【答案】D
【解析】解：因为ab>0，所以a，b同号．
①若a，b同正，则a|a|+b|b|+ab|ab|=1+1+1=3；
②若a，b同负，则a|a|+b|b|+ab|ab|=−1−1+1=−1．
故选：D．
首先根据两数相乘，同号得正，得到a，b符号相同；再根据同正、同负进行分情况讨论．
本题考查了绝对值的性质，要求绝对值里的相关性质要牢记：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0.该题易错点是分析a，b的符号不透彻，漏掉一种情况．
7.【答案】A
【解析】解：c=4+(−1)−5=−2，a=3+(−2)−4=−3，b=4+(−3)+2−1−2=0，
∴a−b+c
=−3−0+(−2)
=−5．
故选：A．
根据第3行和第1列的三个数之和相等，求出c的值是多少，然后根据第1行和第3列的三个数之和相等，求出a的值是多少，最后根据第1行和对角线上的三个数之和相等，求出b的值是多少，再根据有理数加减法的运算方法，求出a−b+c的值是多少即可．
本题考查了有理数的加减法的运算方法，掌握运算法则是解题的关键．
8.【答案】D
【解析】【分析】
本题考查理解题意能力，关键是知道棋子所停的规则，找到规律，然后得到不等式求解．
因棋子移动了k次后走过的总格数是1+2+3+…+k=12k(k+1)，然后根据题目中所给的第k次依次移动k个顶点的规则，可得到不等式最后求得解．
【解答】
解：因棋子移动了k次后走过的总格数是1+2+3+…+k=12k(k+1)，应停在第12k(k+1)−7p格，
这时p是整数，且使0≤12k(k+1)−7p≤6，分别取k=1，2，3，4，5，6，7时，
分别停在1，3，6，3，1，0，0处，发现第2，4，5格没有停棋，
若7由此可知，停棋的情形与k=t时相同，
故第2，4，5格没有停棋，
即：这枚棋子永远不能到达的角的个数是3．
故选D．
9.【答案】5
【解析】解：∵数a在数轴上所对应的点在原点的右边且到原点的距离等于5，
∴这个数a=5，
故答案为：5．
根据已知和点在数轴上的位置得出即可．
本题考查了数轴，能读懂题意是解此题的关键．
10.【答案】4
【解析】解：∵单项式−6x5y和7xm+2yn是同类项，
∴m+2=5，n=1，
解得：m=3，
∴m+n=3+1=4．
故答案为：4．
根据同类项的概念直接得到m、n的值，然后代入求解即可．
本题主要考查同类项的概念，熟记含有字母相同，相同字母的指数也相同的单项式叫做同类项是解题的关键．
11.【答案】43
【解析】解：由题意得：|3m−5|=1，m−2≠0，
解得：m=43．
故答案为：43．
直接利用一元一次方程的定义结合次数与系数的值分析得出答案．
此题主要考查了一元一次方程的定义，正确把握相关定义是解题关键．
12.【答案】±6
【解析】解：由题意得，x2×12=18，
解得x=±6，
故答案为：±6．
根据数值转换机的运算程序，列方程求解即可．
本题考查有理数的混合运算，正确列出方程是解答的前提，求解是解答的关键．
13.【答案】32或−52
【解析】解：∵ab互为倒数，c，d互为相反数，e的绝对值为2，
∴ab=1，c+d=0，e=±2，
当e=2时，c+d5−12ab+e
=05−12×1+2
=0−12+2
=32；
当e=−2时，c+d5−12ab+e
=05−12×1+(−2)
=0−12+(−2)
=−52；
故答案为：32或−52．
根据ab互为倒数，c，d互为相反数，e的绝对值为2，可以得到ab=1，c+d=0，e=±2，然后代入所求式子计算即可．
本题考查有理数的混合运算、绝对值，熟练掌握运算法则是解答本题的关键．
14.【答案】2
【解析】解：根据题意得：3(−2x+1)−2(x−1)=−11，
解得：x=2，．
故答案为：2．
根据新运算法则即可列出方程，求解即可．
本题主要考查新定义、解一元一次方程，解题关键是理解新运算的规律，以此列出方程并求解
15.【答案】−π
【解析】解：∵直径为1个单位长度的圆形纸片上的点A放在数轴的原点上，纸片沿着数轴向左滚动一周，
∴AA′之间的距离为圆的周长=π，
∴A点对应的数是−π．
故答案为：−π．
根据直径为1个单位长度的圆形纸片上的点A放在数轴的原点上，纸片沿着数轴向左滚动一周，得出AA′之间的距离，即可求出答案．
此题考查了数轴，用到的知识点是数轴的特点及圆的周长公式，关键是掌握点的移动与点表示的数之间的关系．
16.【答案】1
【解析】解：将x=1代入原方程得k+2a2−1−bk6=12，
∴3k+6a−1+bk=3，
∴3k+bk=4−6a，
∴(3+b)k=4−6a．
根据题意得：3+b=04−6a=0，
解得：a=23b=−3，
∴6a+b=6×23−3=1．
故答案为：1．
将x=1代入原方程，整理后可得出(3+b)k=4−6a，结合原方程的解与k值无关，可得出关于a，b的方程，解之即可得出a，b的值，再将其代入6a+b中，即可求出结论．
本题考查了一元一次方程的解，牢记“使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解”是解题的关键．
17.【答案】33
【解析】解：令x=1，
所以(3x−1)5=(2)5=32，
∴a0+a1+a2+a3+a4+a5=32，
∵a0=(−1)5=−1，
∴a1+a2+a3+a4+a5
=32−a0
=32−(−1)
=33．
故答案为：33．
求出(3x−1)5的结果，得到a1、a2、a3、a4、a5，计算出它们的和即可．
本题考查了多项式的乘法和有理数的加减运算，确定a1、a2、a3、a4、a5的值是解决本题的关键
18.【答案】665729
【解析】解：由题知，
S①=13；
S②=29=13×23；
S③=427=13×(23)2；
…，
S⑥=13×(23)5；
又因为图形⑦面积是图形⑥面积的2倍，
所以S⑦=2S⑥=64729；
又因为七部分的面积之和为1，
所以S①+S②+S③+…+S⑥=1−S⑦=665729，
即13+29+427+⋯+2536=665729．
故答案为：665729．
利用数形结合的思想即可解决问题．
本题考查图形变化的规律，巧妙利用数形结合的思想是解题的关键．
19.【答案】解：①(−3)−(−1.5)−(−3)+(+3.5)
=−3+1.5+3+3.5
=5；
②(−34−59+712)÷(−136)
=(−34−59+712)×(−36)
=36×34+36×59−36×712
=27+20−21
=47−21
=26；
③−32×[−32×(−23)2−2]
=−32×(−9×49−2)
=−32×(−4−2)
=−32×(−6)
=9；
④−16−16×[3−(−3)2]−2÷(−12)
=−1−16×(3−9)−2×(−2)
=−1−16×(−6)+4
=−1+1+4
=4．
【解析】①按照从左到右的顺序进行计算，即可解答；
②先把有理数的除法转化为乘法，然后再利用乘法分配律进行计算，即可解答；
③先算乘方，再算乘除，后算加减，有括号先算括号里，即可解答；
④先算乘方，再算乘除，后算加减，有括号先算括号里，即可解答．
本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
20.【答案】解：(1)去括号得：6−2x=−4x−20，
移项合并得：2x=−26，
解得：x=−13；
(2)去分母得：6y−3−12=10y−14，
移项合并得：4y=−1，
解得：y=−0.25．
【解析】(1)方程去括号，移项合并，把x系数化为1，即可求出解；
(2)方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．
21.【答案】解：(1)2(x2+3y)−(2x2+3y−x)
=2x2+6y−2x2−3y+x
=3y+x，
当x=1，y=−2时，原式=3×(−2)+1=−5；
(2)5(a2b−3ab2)−2(a2b−7ab2)
=5a2b−15ab2−2a2b+14ab2
=3a2b−ab2，
当a=−1，b=1时，原式=3×(−1)2×1−(−1)×12=3+1=4．
【解析】(1)去括号，合并同类项后代入求值即可；
(2)去括号合并同类项后代入求值即可．
本题考查了整式的加减．合并同类项是关键．
22.【答案】解：(1)15−3+14−11+10−18+14=21(千米)，
答：将最后一名乘客送到目的地时，小张在下午出车点东边，距出发点的距离是21千米．
(2)0.06×(15+3+14+11+10+18+14)×7.5
=0.06×85×7.5
=38.25(元)，
答：这天下午共需支付油费38.25元．
【解析】(1)计算出这些数据的和，即可判断将最后一名乘客送到目的地时，小张离下午出车点的方向和距离，
(2)求出所有数据绝对值的和，即行驶的总路程，再根据耗油量和单价求出总金额．
本题考查有理数的运算在实际中的应用，解答此类题目时要注意总路程为所走路程的绝对值的和．
23.【答案】解：(1)∵m为最小的正整数，且m+n=0，
∴m=1，n=−1，
故A=5x2−mx+n=5x2−x−1，
则A−B=5x2−x−1−(3x2−2x+1)
=5x2−x−1−3x2+2x−1
=2x2+x−2；
(2)A−B=5x2−mx+n−(3x2−2x+1)
=5x2−mx+n−3x2+2x−1
=2x2+(−m+2)x+n−1，
∵A−B的结果中不含一次项和常数项，
∴−m+2=0，n−1=0，
解得：m=2，n=1，
m2+n2−2mn
=22+12−2×2×1
=1．
【解析】(1)直接利用正整数的定义得出m的值，再利用整式的加减运算法则计算得出答案；
(2)整式的加减运算法则计算得出答案．
此题主要考查了整式的加减，正确合并同类项是解题关键．
24.【答案】解：(1)设该中学库存x套桌椅，则x16−20=x16+8；
解得x=960．
答：该中学库存960套桌椅．
(2)设a、b、c三种修理方案的费用分别为y1、y2、y3元，
则y1=(80+10)×96016=5400，
y2=(120+10)×96016+8=5200，
y3=(80+120+10)×96016+16+8=5040，
综上可知，选择方案c更省时省钱．
答：方案c省时省钱．
【解析】此题主要考查了一元一次方程的应用，关键是正确理解题意，找出题目中的等量关系，列出方程．此题要掌握工作量的有关公式：工作总量=工作时间×工作效率．
(1)通过理解题意可知本题的等量关系，即甲单独修完这些桌椅的天数=乙单独修完的天数+20天，列方程求解即可；
(2)分别计算，通过比较选择最省钱的方案．
25.【答案】0 x2+1 x5−x3+x 35
【解析】解：(1)∵整式A是关于x的“奇整式”，当x取1与−1时，对应的整式值分别为A1，A2，
∴A1=−A2，
∴A1+A2=0，
故答案为：0；
(2)①x5−x3+x2+x+1=(x5−x3+x)+(x2+1)，
∵x2+1=(−x)2+1，−(x5−x3+x)=(−x)5−(−x)3+(−x)，
∴x2+1“偶整式”，x5−x3+x是奇整式”，
故答案为：x2+1，x5−x3+x；
②由于x2+1是偶整式，x5−x3+x是奇整式，
∴当x分别取−3，−2，−1，0，1，2，3时，
x2+1的值分别为10，5，2，1，2，5，10；
当x取互为相反数的值时x5−x3+x的值也互为相反数，即和为0，
∴当x分别取−3，−2，−1，0，1，2，3时，x5−x3+x的所有值的和为0，，
∴这七个整式的值之和是10+5+2+1+2+5+10=35；
故答案为：35．
(1)根据定义得到A1=−A2，据此可得答案；
(2)①将原式各项中偶次项和常数项组合在一起即为偶整式，其余项的和即为奇整式；②将各数值依次代入偶整式和奇整式中，再相加即可求解．
本题考查了整式，涉及到了乘方的性质和运算等知识，解题关键是能正确理解偶整式和奇整式的定义，能对整式进行变形以及代入数值进行计算等．
26.【答案】9；2001
【解析】解：(1)由图中关系可得：当a=1，S取最小值，m=9；当d=2009时S取得最大值，m=2001．
(2)根据图中关系，可知a=m−8，b=m−6，c=m+6，d=m+8．
因为每排为7个数，m与上列正对的数表示为m−7，
所以可得与上列正对数相邻数的表示方法为m−6，m−8；
同理m与下列正对的数差为+7，即可得与下列正对数相邻数的表示方法m+6，m+8．
(3)由(2)题可知S=4m，当S=240，m=60．
(4)不能；设和等于588时，4m=588，解得m=147，
因为m为7的倍数时在最右列，故不符合要求，所以四数的和不能为488．
(1)当a=1，S取最小值，m=9；当d=2009时S取得最大值，m=2001．
(2)根据图中关系，可知a=m−8，b=m−6，c=m+6，d=m+8．
(3)由(2)题可知S=5m，当S=240，求m的值即可．
(4)同(3)理解得m的值，注意m不能为四个边上的任一数．
本题考查了列代数式的应用，并考查了学生的阅读理解及总结规律的能力，是一道综合性的题目．
27.【答案】4 16
【解析】解：(1)∵(a−4)2+|16−b|=0，
∴a−4=0，16−b=0，
∴a=4，b=16，
故答案为：4，16；
(2)设运动时间为t s，
由题意得，3t=2(16−4−3t)或3t=2(4+3t−16)，
解得t=83或8，
∴运动时间为83或8秒时，点P到点A的距离是点P到点B的距离的2倍；
(3)设点P和点Q运动t秒时，P、Q两点之间的距离为4，
如图1，当点Q在点P右侧，
12+t−3t=4，
解得t=4，
如图2，当点P在点Q的右侧，
3t−(12+t)=4，
解得t=8，
如图3，当点P从点C返回时，且点P在Q的右侧，
12+t+4+3t=52，
解得t=9，
如图4，当点P返回时，点Q在点P的右侧，
12+t+3t−4=52，
解得t=11，
即点P和点Q运动4或8或9或11秒时，P、Q两点之间的距离为4，
此时点Q表示的数为20、24、25、27．
(1)根据非负数的性质可得a−4=0，16−b=0，即可求解；
(2)设运动时间为t s，由题意构建方程求解即可；
(3)根据点P和点Q的位置分四种情况建立方程计算即可．
本题考查数轴及行程问题的应用，解题的关键是构建方程，运用分类讨论的思想解决问题．