22，河南省信阳市淮滨县2023-2024学年下学期入学学情调研测试八年级数学试题

这是一份22，河南省信阳市淮滨县2023-2024学年下学期入学学情调研测试八年级数学试题，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共30分）
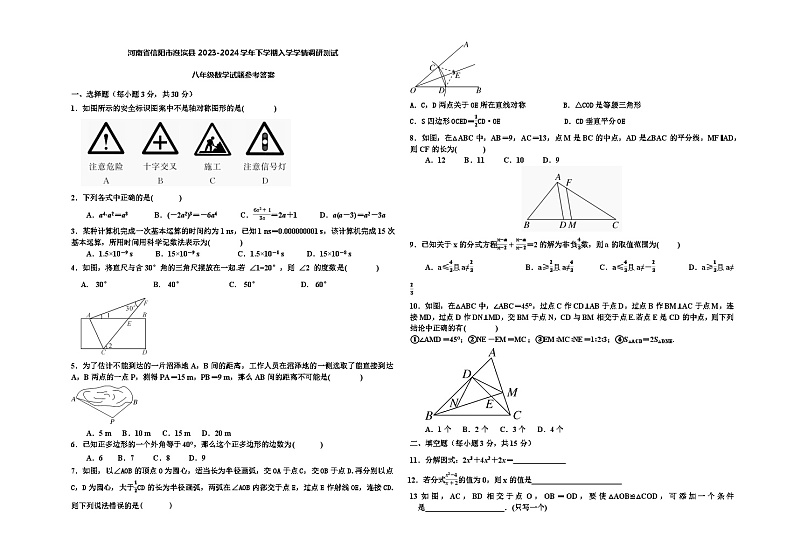
1．如图所示的安全标识图案中不是轴对称图形的是( )
2．下列各式中正确的是( )
A．a4·a2＝a8 B．(－2a2)3＝－6a6 C．6a²+13a＝2a＋1 D．a(a－3)＝a2－3a
3．某种计算机完成一次基本运算的时间约为1 ns，已知1 ns＝0.000000001 s，该计算机完成15次基本运算，所用时间用科学记数法表示为( )
A．1.5×10－9 s B．15×10－9 s C．1.5×10－8 s D．15×10－8 s
4．如图，将直尺与含30°角的三角尺摆放在一起.若 ∠1=20°，则 ∠2 的度数是( )
A. 30°B. 40°C. 50°D. 60°
5．为了估计不能到达的一片沼泽地A，B间的距离，工作人员在沼泽地的一侧选取了能直接到达A，B两点的一点P，测得PA＝15 m，PB＝9 m，那么AB间的距离不可能是( )
A．5 m B．10 m C．15 m D．20 m
6．已知正多边形的一个外角等于40°，那么这个正多边形的边数为( )
A．6 B．7 C．8 D．9
7．如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D.再分别以点C，D为圆心，大于12CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD.则下列说法错误的是( )
C，D两点关于OE所在直线对称 B．△COD是等腰三角形
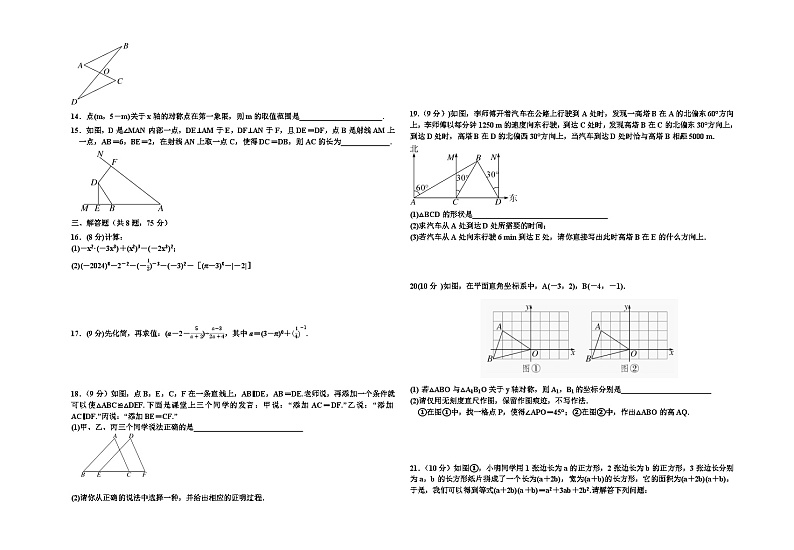
C．S四边形OCED＝12CD·OE D．CD垂直平分OE
8．如图，在△ABC中，AB＝9，AC＝13，点M是BC的中点，AD是∠BAC的平分线，MF∥AD，则CF的长为( )
A．12 B．11 C．10 D．9
9．已知关于x的分式方程x−ax−2+x−ax−2＝2的解为非负43数，则a的取值范围为( )
A．a≤43且a≠23 B．a≥23且a≠43 C．a≤43且a≠－23 D．a≥13且a≠23
10．如图，在△ABC中，∠ABC＝45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，连接MD，过点D作DN⊥MD，交BM于点N，CD与BM相交于点E.若点E是CD的中点，则下列结论中正确的有( )
①∠AMD＝45°；②NE－EM＝MC；③EM∶MC∶NE＝1∶2∶3；④S△ACD＝2S△DNE.
A．1个 B．2个 C．3个 D．4个
二、填空题（每小题3分，共15分）
11．分解因式：2x3＋4x2＋2x＝
12．若分式x²−4x+2的值为0，则x的值是
13如图，AC，BD相交于点O，OB＝OD，要使△AOB≌△COD，可添加一个条件是 ．(只写一个)
14．点(m，5－m)关于x轴的对称点在第一象限，则m的取值范围是 .
15．如图，D是∠MAN内部一点，DE⊥AM于E，DF⊥AN于F，且DE＝DF，点B是射线AM上一点，AB＝6，BE＝2，在射线AN上取一点C，使得DC＝DB，则AC的长为 .
三、解答题（共8题，75分）
16．(8分)计算：
(1)－x2·(－3x3)＋(x2)3－(－2x3)2；
(2)(－2024)0－2－2－(－12)－3－(－3)2－［(π－3)0－|－2|］
17．(9分)先化简，再求值：(a－2－5a+2)÷a−32a+4，其中a＝(3－π)0＋(14)−1.
18．（9分）如图，点B，E，C，F在一条直线上，AB∥DE，AB＝DE.老师说，再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言：甲说：“添加AC＝DF.”乙说：“添加AC∥DF.”丙说：“添加BE＝CF.”
(1)甲、乙、丙三个同学说法正确的是
(2)请你从正确的说法中选择一种，并给出相应的证明过程．
19.（9分）)如图，李师傅开着汽车在公路上行驶到A处时，发现一高塔B在A的北偏东60°方向上，李师傅以每分钟1250 m的速度向东行驶，到达C处时，发现高塔B在C的北偏东30°方向上，到达D处时，高塔B在D的北偏西30°方向上，当汽车到达D处时恰与高塔B相距5000 m.
(1)△BCD的形状是
(2)求汽车从A处到达D处所需要的时间；
(3)若汽车从A处向东行驶6 min到达E处，请你直接写出此时高塔B在E的什么方向上．
20(10分 )如图，在平面直角坐标系中，A(－3，2)，B(－4，－1)．
若△ABO与△A1B1O关于y轴对称，则A1，B1的坐标分别是
(2)请仅用无刻度直尺作图，保留作图痕迹，不写作法．
①在图①中，找一格点P，使得∠APO＝45°；②在图②中，作出△ABO的高AQ.
21．（10分）如图①，小明同学用1张边长为a的正方形，2张边长为b的正方形，3张边长分别为a，b的长方形纸片拼成了一个长为(a＋2b)，宽为(a＋b)的长方形，它的面积为(a＋2b)(a＋b)，于是，我们可以得到等式(a＋2b)(a＋b)＝a2＋3ab＋2b2.请解答下列问题：
根据图②，写出一个恒等式；
(2)利用(1)中所得到的结论，解决下面的问题：已知a＋b＋c＝10，a2＋b2＋c2＝40，求ab＋bc＋ac的值；
(3)小明同学又用4张边长为a的正方形，3张边长为b的正方形，8张边长分别为a，b的长方形纸片拼出了一个长方形，那么该长方形的长为 ，宽为
22．（10分）某校在商场购进A，B两种品牌的篮球，购买A品牌篮球花费了2500元，购买B品牌篮球花费了2000元，且购买A品牌篮球数量是购买B品牌篮球数量的2倍，已知购买一个B品牌篮球比购买一个A品牌篮球多花30元．
(1)购买一个A品牌、一个B品牌的篮球各需多少元？
(2)该校决定再次购进A，B两种品牌篮球共50个，恰逢商场对两种品牌篮球的售价进行调整，A品牌篮球的售价比第一次购买时提高了8%，B品牌篮球按第一次购买时售价的9折出售，如果该校此次购买A，B两种品牌篮球的总费用不超过3060元，那么该校此次最多可购买多少个B品牌篮球？
23．（10分）新知学习：若一条线段把一个平面图形分成面积相等的两部分，我们把这条线段叫做该平面图形的二分线．解决问题：
(1)①三角形的中线、高、角平分线中，一定是三角形的二分线的是
②如图①，已知△ABC中，AD是BC边上的中线，点E，F分别在AB，DC上，连接EF，与AD交于点G.若S△AEG＝S△DGF，则EF (选填“是”或“不是”)△ABC的一条二分线，并说明理由；
(2)如图②，四边形ABCD中，CD平行于AB，点G是AD的中点，射线CG交射线BA于点E，取EB的中点F，连接CF.求证：CF是四边形ABCD的二分线．
河南省信阳市淮滨县2023-2024学年下学期入学学情调研测试
八年级数学试题参考答案
一、选择题（每小题3分，共30分）
1．如图所示的安全标识图案中不是轴对称图形的是( C )
2．下列各式中正确的是( D )
A．a4·a2＝a8 B．(－2a2)3＝－6a6 C．6a²+13a＝2a＋1 D．a(a－3)＝a2－3a
3．某种计算机完成一次基本运算的时间约为1 ns，已知1 ns＝0.000000001 s，该计算机完成15次基本运算，所用时间用科学记数法表示为( C )
A．1.5×10－9 s B．15×10－9 s C．1.5×10－8 s D．15×10－8 s
4．如图，将直尺与含30°角的三角尺摆放在一起.若 ∠1=20°，则 ∠2 的度数是( C )
A. 30°B. 40°C. 50°D. 60°
5．为了估计不能到达的一片沼泽地A，B间的距离，工作人员在沼泽地的一侧选取了能直接到达A，B两点的一点P，测得PA＝15 m，PB＝9 m，那么AB间的距离不可能是( A )
A．5 m B．10 m C．15 m D．20 m
6．已知正多边形的一个外角等于40°，那么这个正多边形的边数为( D )
A．6 B．7 C．8 D．9
7．如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D.再分别以点C，D为圆心，大于12CD的长为半径画弧，两弧在∠AOB内部交于点E，过点E作射线OE，连接CD.则下列说法错误的是( D )
C，D两点关于OE所在直线对称 B．△COD是等腰三角形
C．S四边形OCED＝12CD·OE D．CD垂直平分OE
8．如图，在△ABC中，AB＝9，AC＝13，点M是BC的中点，AD是∠BAC的平分线，MF∥AD，则CF的长为( B )
A．12 B．11 C．10 D．9
9．已知关于x的分式方程x−ax−2+x−ax−2＝2的解为非负43数，则a的取值范围为( A )
A．a≤43且a≠23 B．a≥23且a≠43 C．a≤43且a≠－23 D．a≥13且a≠23
10．如图，在△ABC中，∠ABC＝45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，连接MD，过点D作DN⊥MD，交BM于点N，CD与BM相交于点E.若点E是CD的中点，则下列结论中正确的有( C )
①∠AMD＝45°；②NE－EM＝MC；③EM∶MC∶NE＝1∶2∶3；④S△ACD＝2S△DNE.
A．1个 B．2个 C．3个 D．4个
二、填空题（每小题3分，共15分）
11．分解因式：2x3＋4x2＋2x＝ 2x(x＋1)2
12．若分式x²−4x+2的值为0，则x的值是 2 .
13如图，AC，BD相交于点O，OB＝OD，要使△AOB≌△COD，可添加一个条件是 OA＝OC(答案不唯一) ．(只写一个)
14．点(m，5－m)关于x轴的对称点在第一象限，则m的取值范围是 m＞5 .
15．如图，D是∠MAN内部一点，DE⊥AM于E，DF⊥AN于F，且DE＝DF，点B是射线AM上一点，AB＝6，BE＝2，在射线AN上取一点C，使得DC＝DB，则AC的长为 6或10 .
三、解答题（共8题，75分）
16．(8分)计算：
(1)－x2·(－3x3)＋(x2)3－(－2x3)2；
解：原式＝3x5＋x6－4x6＝3x5－3x6.(4分)
(2)(－2024)0－2－2－(－12)－3－(－3)2－［(π－3)0－|－2|］＝34
解：原式＝－14－(－1)＝34 .(4分)
17．(9分)先化简，再求值：(a－2－5a+2)÷a−32a+4，其中a＝(3－π)0＋(14)−1.
解：原式＝2a＋6.∵a＝(3－π)0＋(14)−1＝1＋4＝5，∴原式＝2×5＋6＝16.(9分)
18．（9分）如图，点B，E，C，F在一条直线上，AB∥DE，AB＝DE.老师说，再添加一个条件就可以使△ABC≌△DEF.下面是课堂上三个同学的发言：甲说：“添加AC＝DF.”乙说：“添加AC∥DF.”丙说：“添加BE＝CF.”
(1)甲、乙、丙三个同学说法正确的是 乙、丙 ；(3分)
(2)请你从正确的说法中选择一种，并给出相应的证明过程．
解：选择乙同学的说法，证明：
∵AB∥DE，∴∠B＝∠DEF.
∵AC∥DF，∴∠F＝∠ACB.
在△ABC和△DEF中，
∴△ABC≌△DEF(AAS)．(9分)
19.（9分）)如图，李师傅开着汽车在公路上行驶到A处时，发现一高塔B在A的北偏东60°方向上，李师傅以每分钟1250 m的速度向东行驶，到达C处时，发现高塔B在C的北偏东30°方向上，到达D处时，高塔B在D的北偏西30°方向上，当汽车到达D处时恰与高塔B相距5000 m.
(1)△BCD的形状是 等边三角形 ；(2分)
(2)求汽车从A处到达D处所需要的时间；
解：由题意可知∠BAD＝90°－60°＝30°，
∠BDA＝90°－30°＝60°.
在△ABD中，∠ABD＝180°－∠BAD－∠BDA＝90°，∴AD＝2BD＝10000(m)．
∴汽车从A处到达D处所需要的时间为100001250＝8(min)．(6分)
(3)若汽车从A处向东行驶6 min到达E处，请你直接写出此时高塔B在E的什么方向上．
解：由题意可知∠BCD＝∠BDC＝60°，∴∠CBD＝60°.
∴△BCD是等边三角形．∴CD＝BD＝5000 m.
∵AE＝1250×6＝7500(m)，
∴DE＝AD－AE＝2500 m.
∴CE＝CD－DE＝2500 m．
∴E为CD的中点．
∴BE⊥CD，即高塔B在E的正北方向上．(9分)
20(10分 )如图，在平面直角坐标系中，A(－3，2)，B(－4，－1)．
(1)若△ABO与△A1B1O关于y轴对称，则A1，B1的坐标分别是 (3，2)，(4，－1) ；(2分)
(2)请仅用无刻度直尺作图，保留作图痕迹，不写作法．
①在图①中，找一格点P，使得∠APO＝45°；②在图②中，作出△ABO的高AQ.
解：(2)①如图①所示，点P即为所求．(6分)
②如图②所示，线段AQ即为所求．(10分)
21．（10分）如图①，小明同学用1张边长为a的正方形，2张边长为b的正方形，3张边长分别为a，b的长方形纸片拼成了一个长为(a＋2b)，宽为(a＋b)的长方形，它的面积为(a＋2b)(a＋b)，于是，我们可以得到等式(a＋2b)(a＋b)＝a2＋3ab＋2b2.请解答下列问题：
(1)根据图②，写出一个恒等式；
解：(a＋b＋c)2＝a2＋b2＋c2＋2ab＋2bc＋2ac.(2分)
(2)利用(1)中所得到的结论，解决下面的问题：已知a＋b＋c＝10，a2＋b2＋c2＝40，求ab＋bc＋ac的值；
解：∵a＋b＋c＝10，∴(a＋b＋c)2＝100.
又∵(a＋b＋c)2＝a2＋b2＋c2＋2ab＋2bc＋2ac，
∴ab＋bc＋ac＝12[(a＋b＋c)2－(a2＋b2＋c2)]＝12×(100－40)＝30.(8分)
(3)小明同学又用4张边长为a的正方形，3张边长为b的正方形，8张边长分别为a，b的长方形纸片拼出了一个长方形，那么该长方形的长为 2a＋3b ，宽为 2a＋b . (10分)
22．（10分）某校在商场购进A，B两种品牌的篮球，购买A品牌篮球花费了2500元，购买B品牌篮球花费了2000元，且购买A品牌篮球数量是购买B品牌篮球数量的2倍，已知购买一个B品牌篮球比购买一个A品牌篮球多花30元．
(1)购买一个A品牌、一个B品牌的篮球各需多少元？
解：设购买一个A品牌的篮球需x元，
则购买一个B品牌的篮球需(x＋30)元，由题意得2500x＝2×2000x+30，解得x＝50，
经检验，x＝50是原方程的解，且符合题意，
则x＋30＝80.
答：购买一个A品牌的篮球需50元，购买一个B品牌的篮球需80元．(5分)
(2)该校决定再次购进A，B两种品牌篮球共50个，恰逢商场对两种品牌篮球的售价进行调整，A品牌篮球的售价比第一次购买时提高了8%，B品牌篮球按第一次购买时售价的9折出售，如果该校此次购买A，B两种品牌篮球的总费用不超过3060元，那么该校此次最多可购买多少个B品牌篮球？
解：设该校此次可购买a个B品牌篮球，则购进A品牌篮球(50－a)个，由题意得50×(1＋8%)(50－a)＋80×0.9a≤3060，解得a≤20.
答：该校此次最多可购买20个B品牌篮球．(10分)
23．（10分）新知学习：若一条线段把一个平面图形分成面积相等的两部分，我们把这条线段叫做该平面图形的二分线．解决问题：
(1)①三角形的中线、高、角平分线中，一定是三角形的二分线的是 三角形的中线 ；(2分)
②如图①，已知△ABC中，AD是BC边上的中线，点E，F分别在AB，DC上，连接EF，与AD交于点G.若S△AEG＝S△DGF，则EF 是 (选填“是”或“不是”)△ABC的一条二分线，并说明理由；(3分)
解：理由如下：
∵AD是BC边上的中线，
∴S△ABD＝S△ACD＝12S△ABC.
∵S△AEG＝S△DGF，
∴S四边形BDGE＋S△AEG＝S四边形BDGE＋S△DGF.
∴S△BEF＝S△ABD＝12S△ABC.
∴EF是△ABC的一条二分线．(6分)
(2)如图②，四边形ABCD中，CD平行于AB，点G是AD的中点，射线CG交射线BA于点E，取EB的中点F，连接CF.求证：CF是四边形ABCD的二分线．
证明：∵F是EB的中点，
∴S△CBF＝S△CEF.
∵AB∥DC，∴∠E＝∠DCG.
∵G是AD的中点，∴DG＝AG.
在△EAG和△CDG中，
∴△EAG≌△CDG(AAS)．
∴S△AEG＝S△DCG.
∴S四边形AFCD＝S△CEF.
∴S四边形AFCD＝S△CBF.
∴CF是四边形ABCD的二分线．(10分)