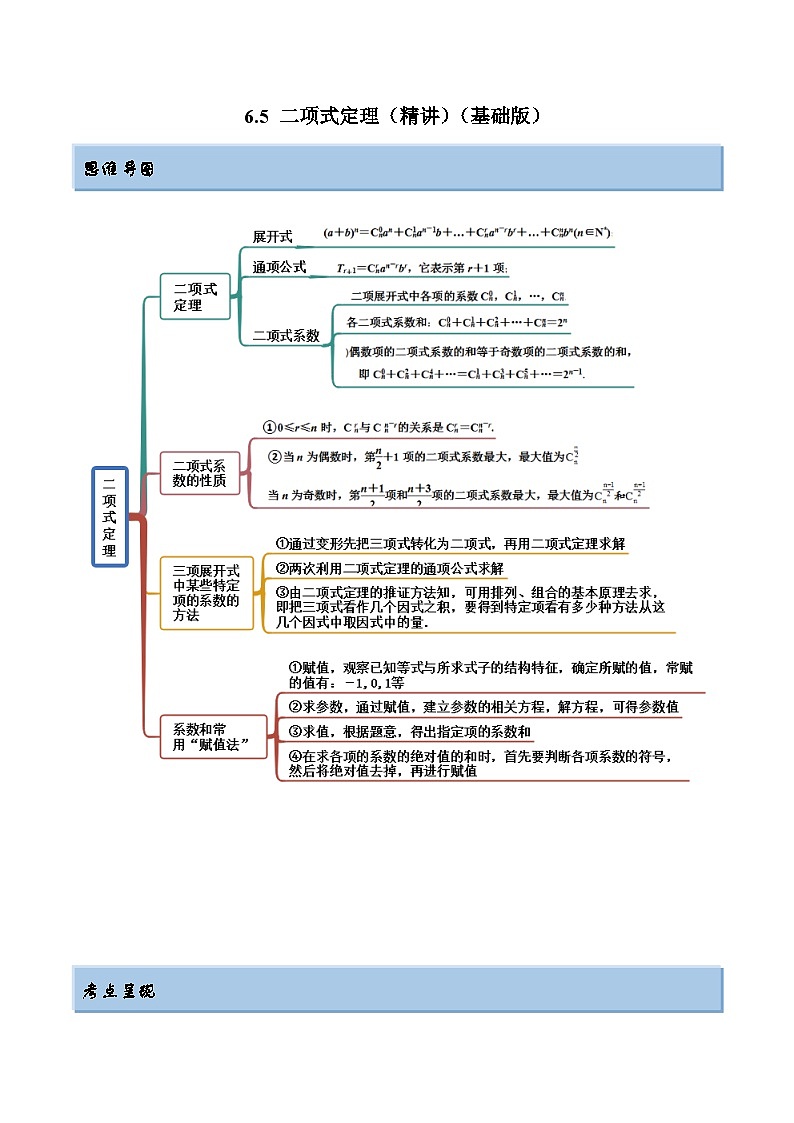
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.5 二项式定理（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.5 二项式定理（精讲）（基础版）（原卷版+解析版），共15页。试卷主要包含了指定项系数，二项式相乘的系数，三项式的系数，系数和等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 指定项系数
【例1-1】 (2023·全国·高三专题练习（理））的展开式中的系数为（ ）
A．10B．20C．40D．80
【例1-2】 (2023·广东惠州·高三阶段练习）展开式中的常数项为（ ）
A．480B．C．240D．260
【例1-3】 (2023·湖北武汉·高三开学考试）若二项式的展开式中的系数是84，则实数（ ）
A．2B．C．1D．
【例1-4】 (2023·江苏无锡·模拟预测）二项式的展开式中，含项的二项式系数为（ ）
A．84B．56C．35D．21
【例1-5】 (2023·广西·南宁二中高三阶段练习（理））二项式展开式中，有理项共有（ ）项．
A．3B．4C．5D．7
【一隅三反】
1． (2023·北京昌平·高三期末）在的展开式中，的系数为（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）若，则（ ）
A．-448B．-112C．112D．448
3． (2023·陕西·宝鸡中学模拟预测（理））二项式的展开式中，其中是无理项的项数共有（ ）
A．项B．项C．项D．项
4． (2023·广东·高三阶段练习）的展开式中，的系数为，则___________．
考点二 二项式相乘的系数
【例2】 (2023·四川省泸县第一中学）的展开式中含的项的系数为（ ）
A．10B．15C．20D．25
【一隅三反】
1． (2023·江苏·常州高级中学模拟预测）的展开式中的系数为（ ）
A．B．25C．D．5
2． (2023·山东·德州市教育科学研究院三模）的展开式中的系数为（ ）
A．80B．24C．D．
3． (2023·天津河西·三模）的展开式中，的系数是__________.
考点三 三项式的系数
【例3-1】 (2023·江苏泰州·模拟预测）的展开式中，项的系数为（ ）
A．400B．480C．720D．800
【例3-2】 (2023·全国·高三专题练习）若的展开式中的系数为35，则正数（ ）
A．B．2C．D．4
【一隅三反】
1． (2023·全国·模拟预测）的展开式中，的系数为（ ）
A． B．C．D．
2． (2023·全国·高三专题练习（理））的展开式中，含项的系数为______.
3． (2023·陕西·宝鸡中学模拟预测（理））的展开式中的系数是___________（用数字作答）
考点四 系数和
【例4】 (2023·全国·高三专题练习）已知，求：
（1）；
（2）；
（3）；
（4）.
【一隅三反】
1． (2023·全国·高三专题练习）在(2x－3y)10的展开式中，求：
(1)二项式系数的和；
(2)各项系数的和；
(3)奇数项的二项式系数和与偶数项的二项式系数和；
(4)奇数项系数和与偶数项系数和.
2． (2023·全国·高三专题练习）在的展开式中，求：
（1）二项式系数的和；
（2）各项系数的和；
（3）奇数项的二项式系数和与偶数项的二项式系数和；
（4）奇数项系数和与偶数项系数和；
（5）的奇次项系数和与的偶次项系数和.
6.5 二项式定理（精讲）（基础版）
思维导图
考点呈现
例题剖析
考点一 指定项系数
【例1-1】 (2023·全国·高三专题练习（理））的展开式中的系数为（ ）
A．10B．20C．40D．80
【答案】C
【解析】二项式展开式的通式为，由，得r＝2，此时
即的展开式中的系数为40故选：C
【例1-2】 (2023·广东惠州·高三阶段练习）展开式中的常数项为（ ）
A．480B．C．240D．260
【答案】C
【解析】展开式的通项为：，
令，解得，所以展开式的常数项为；故选：C
【例1-3】 (2023·湖北武汉·高三开学考试）若二项式的展开式中的系数是84，则实数（ ）
A．2B．C．1D．
【答案】B
【解析】二项式展开式的第项为.
又展开式中的系数是84，即.所以，解得故选：B.
【例1-4】 (2023·江苏无锡·模拟预测）二项式的展开式中，含项的二项式系数为（ ）
A．84B．56C．35D．21
【答案】B
【解析】因为二项式为，
所以其展开式中，含项的二项式系数为：
，，，，，.
故选：B
【例1-5】 (2023·广西·南宁二中高三阶段练习（理））二项式展开式中，有理项共有（ ）项．
A．3B．4C．5D．7
【答案】D
【解析】二项式展开式中，通项为，其中，
的取值只需满足，则，即有理项共有7项，故选：D.
【一隅三反】
1． (2023·北京昌平·高三期末）在的展开式中，的系数为（ ）
A．B．C．D．
【答案】D
【解析】的通项为，
令，即，，故选：D.
2． (2023·全国·高三专题练习）若，则（ ）
A．-448B．-112C．112D．448
【答案】C
【解析】，.
故选：C.
3． (2023·陕西·宝鸡中学模拟预测（理））二项式的展开式中，其中是无理项的项数共有（ ）
A．项B．项C．项D．项
【答案】D
【解析】二项式的展开式中，通项公式为，
，时为有理项共6项，故无理项的项数共有故选：D.
4． (2023·广东·高三阶段练习）的展开式中，的系数为，则___________．
【答案】
【解析】的展开式中的第项为：，
令，则，解得，即；故答案为：
考点二 二项式相乘的系数
【例2】 (2023·四川省泸县第一中学）的展开式中含的项的系数为（ ）
A．10B．15C．20D．25
【答案】B
【解析】的展开式的通项为，
则的展开式中含的项是，
所以的展开式中含的项的系数为15.故选：B
【一隅三反】
1． (2023·江苏·常州高级中学模拟预测）的展开式中的系数为（ ）
A．B．25C．D．5
【答案】A
【解析】∵
的展开式为，
令，得，则，
令，得，则，
令，得，
∴的展开式中的系数为.
故选：A．
2． (2023·山东·德州市教育科学研究院三模）的展开式中的系数为（ ）
A．80B．24C．D．
【答案】A
【解析】依题意，，显然展开式中没有项，
展开式的项为，
所以的展开式中的系数为80.故选：A
3． (2023·天津河西·三模）的展开式中，的系数是__________.
【答案】
【解析】的展开式的通项，
令，得，；
令，得，，
则的展开式中的系数是．
故答案为：
考点三 三项式的系数
【例3-1】 (2023·江苏泰州·模拟预测）的展开式中，项的系数为（ ）
A．400B．480C．720D．800
【答案】D
【解析】，
的展开式通项为，的展开式通项为，
所以的展开式通项为，
其中，，且、，令，可得或或，
因此的展开式中的系数为.故选：D.
【例3-2】 (2023·全国·高三专题练习）若的展开式中的系数为35，则正数（ ）
A．B．2C．D．4
【答案】B
【解析】因为展开式为：，
即
，
所以，
，
，
所以含的系数为，又为正数，所以.故选：B.
【一隅三反】
1． (2023·全国·模拟预测）的展开式中，的系数为（ ）
A． B．C．D．
【答案】D
【解析】可看作5个因式相乘，
所以其展开式中含的项为4个因式取，2个因式取，
所以展开式中含的系数为．故选：D．
2． (2023·全国·高三专题练习（理））的展开式中，含项的系数为______.
【答案】
【解析】展开式的通项为，
令，则展开式中含的项为，
所以含项的系数为.
3． (2023·陕西·宝鸡中学模拟预测（理））的展开式中的系数是___________（用数字作答）
【答案】
【解析】
展开式通项为：；展开式通项为：；
则当，时，的系数为；当，时，的系数为；当，时，的系数为；当，时，的系数为；
的展开式中的系数为.
故答案为：.
考点四 系数和
【例4】 (2023·全国·高三专题练习）已知，求：
（1）；
（2）；
（3）；
（4）.
【答案】（1）-2；（2）-1094；（3）1093；（4）2187.
【解析】解：令则①；
令则②；
令则③；
（1）②-①得：；
（2）(②-③)得：；
（3）(②+③)得：；
（4）由展开式可知均为负值，均为正值，
则.
【一隅三反】
1． (2023·全国·高三专题练习）在(2x－3y)10的展开式中，求：
(1)二项式系数的和；
(2)各项系数的和；
(3)奇数项的二项式系数和与偶数项的二项式系数和；
(4)奇数项系数和与偶数项系数和.
【答案】(1)210(2)1(3)29，29(4)奇数项系数和为，偶数项系数和为
【解析】(1)二项式系数的和为.
(2)令x＝y＝1，各项系数和为(2－3)10＝(－1)10＝1.
(3)奇数项的二项式系数和为，偶数项的二项式系数和为.
(4)设(2x－3y)10＝a0x10＋a1x9y＋a2x8y2＋…＋a10y10
令x＝y＝1，得到a0＋a1＋a2＋…＋a10＝1，①
令x＝1，y＝－1(或x＝－1，y＝1)，得a0－a1＋a2－a3＋…＋a10＝510，②
其中①＋②得：，∴奇数项系数和为；①－②得：，∴偶数项系数和为.
2． (2023·全国·高三专题练习）在的展开式中，求：
（1）二项式系数的和；
（2）各项系数的和；
（3）奇数项的二项式系数和与偶数项的二项式系数和；
（4）奇数项系数和与偶数项系数和；
（5）的奇次项系数和与的偶次项系数和.
【答案】（1）；
（2）1；
奇数项的二项式系数和为，偶数项的二项式系数和为；
奇数项的系数和为，偶数项的系数和为；
（5）的奇次项系数和为，的偶次项系数和为
【解析】设，
各项系数和为，
奇数项系数和为，偶数项系数和为，
的奇次项系数和为，的偶次项系数和为
（1）二项式系数的和为；
（2）令，，则，
所以各项系数和为1；
（3）奇数项的二项式系数和为，
偶数项的二项式系数和为；
（4）由（2）知，①，取，，
则②，
所以奇数项的系数和，
偶数项的系数和；
（5）由（4）知，的奇次项系数和为，
的偶次项系数和为.