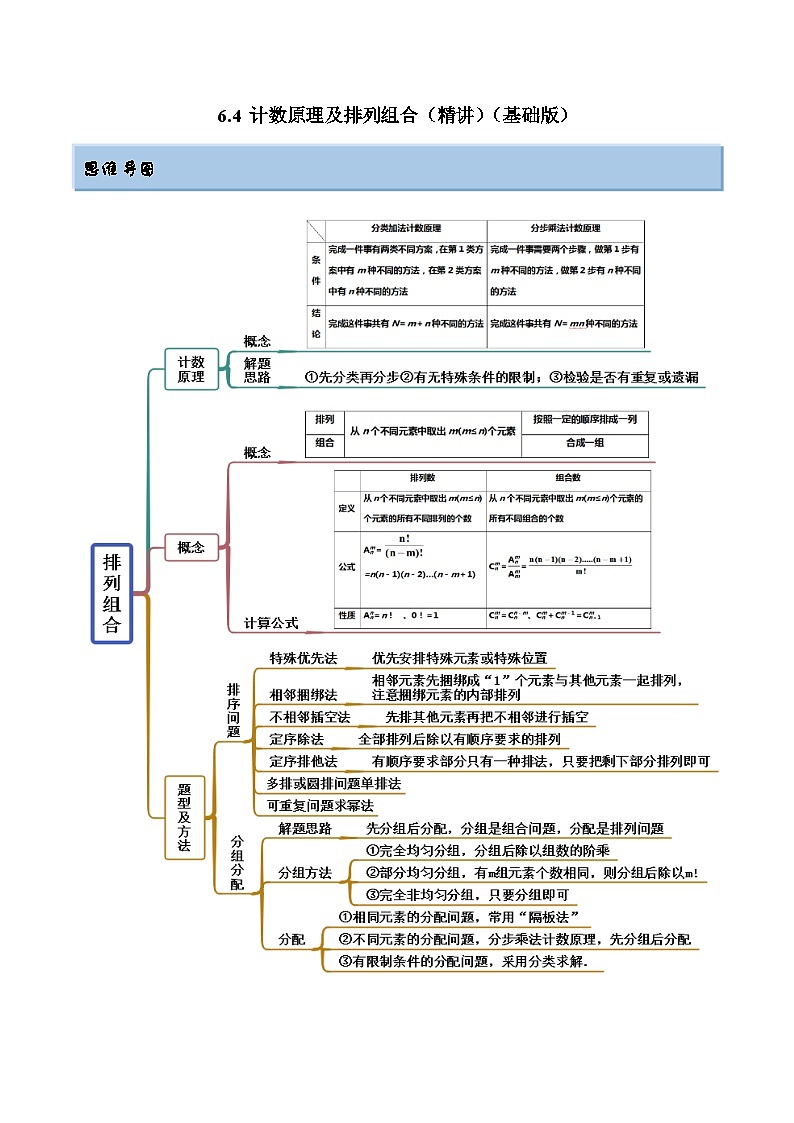
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.4 计数原理及排列组合（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.4 计数原理及排列组合（精讲）（基础版）（原卷版+解析版），共22页。试卷主要包含了排队问题，排数问题，分组分配，涂色等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 排队问题
【例1】 (2023·广东）有7名同学，其中3名男生、4名女生，求在下列不同条件下的排法种数．
(1)选5人排成一排；
(2)全体站成一排，女生互不相邻；
(3)全体站成一排，其中甲不站在最左边，也不站在最右边；
(4)全体站成一排，其中甲不站在最左边，乙不站在最右边；
(5)男生顺序已定，女生顺序不定；
(6)站成三排，前排2名同学，中间排3名同学，后排2名同学，其中甲站在中间排的中间位置；
(7)7名同学站成一排，其中甲、乙相邻，但都不与丙相邻；
(8)7名同学坐圆桌吃饭，其中甲、乙相邻．
【一隅三反】
1． (2023·河北·藁城新冀明中学）有名男生和甲、乙名女生排成一排，求下列情况各有多少种不同的排法？
(1)女生甲排在正中间；
(2)名女生不相邻；
(3)女生甲必须排在女生乙的左边（不一定相邻）；
(4)名女生中间恰有名男生．
2． (2023·全国·高三专题练习）某种产品的加工需要经过道工序．
(1)如果工序不能放在最后，那么有多少种加工顺序？（数字作答）
(2)如果工序必须相邻，那么有多少种加工顺序？（数字作答）
(3)如果工序C，D必须不能相邻，那么有多少种加工顺序？（数字作答）
3． (2023·全国·高三专题练习）现有8个人男3女）站成一排.
(1)女生必须排在一起，共有多少种不同的排法？
(2)其中甲必须站在排头有多少种不同排法？
(3)其中甲、乙两人不能排在两端有多少种不同的排法？
(4)其中甲、乙两人不相邻有多少种不同的排法？
(5)其中甲在乙的左边有多少种不同的排法？
(6)其中甲乙丙不能彼此相邻，有多少种不同排法？
(7)男生在一起，女生也在一起，有多少种不同排法？
(8)第3和第6个排男生，有多少种不同排法？
(9)甲乙不能排在前3位，有多少种不同排法？
(10)女生两旁必须有男生，有多少种不同排法？
考点二 排数问题
【例2】 (2023·江苏）用0，1，2，3，4这五个数字组成无重复数字的自然数．
（1）在组成的五位数中，所有奇数的个数有多少?
（2）在组成的五位数中，数字1和3相邻的个数有多少?
（3）在组成的五位数中，若从小到大排列，30124排第几个?
【一隅三反】
1． (2023·吉林）从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数．
试问：（1）能组成多少个不同的五位偶数？
（2）五位数中，两个偶数排在一起的有几个？
（3）两个偶数不相邻且三个奇数也不相邻的五位数有几个？（所有结果均用数值表示）
2．（2022·全国·高三专题练习）用数字1，2，3，4，5组成没有重复数字的数，问
（1）能够组成多少个五位奇数？
（2）能够组成多少个正整数？
（3）能够组成多少个大于40000的正整数？
3． (2023·民大附中海南陵水分校）用0、1、2、3、4五个数字:
(1)可组成多少个五位数；
(2)可组成多少个无重复数字的五位数；
(3)可组成多少个无重复数字的且是3的倍数的三位数；
(4)可组成多少个无重复数字的五位奇数．
考点三 分组分配
【例3】 (2023·全国·高三专题练习）按下列要求分配6本不同的书,各有多少种不同的分配方式?
（1）分成三份,1份1本,1份2本,1份3本;
（2）甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
（3）平均分成三份,每份2本;
（4）平均分配给甲、乙、丙三人,每人2本;
（5）分成三份,1份4本,另外两份每份1本;
（6）甲、乙、丙三人中,一人得4本,另外两人每人得1本;
（7）甲得1本,乙得1本,丙得4本.
【一隅三反】
1．（2023·全国·高三专题练习）为宣传城市文化，提高城市知名度，我市某所学校5位同学各自随机从“趵突腾空”、“ 历山览胜”、“明湖汇泊”三个城市推荐词中选择一个，来确定该学校所推荐的景点，则三个推荐词都有人选的概率是（ ）
A．B．C．D．
2． (2023·河北·邢台市南和区第一中学）某研究机构采访了“—带一路”沿线20国的青年，让他们用一个关键词表达对中国的印象，使用频率前12的关键词为高铁，移动支付，网购，共享单车、一带一路、无人机、大熊猫、广场舞、中华美食、长城、京剧、美丽乡村．其中使用频率排前4的关键词“高铁、移动支付、网购、共享单车”也成为了他们眼中的“新四大发明”．若将这12个关键词平均分成3组，且各组都包含“新四大发明”关键词．则不同的分法种数为（ ）
A．1680B．3360C．6720D．10080
3． (2023·河北省曲阳县第一高级中学）某地区安排A，B，C，D，E，F六名党员志愿者同志到三个基层社区开展防诈骗宣传活动，每个地区至少安排一人，至多安排三人，且A，B两人安排在同一个社区，C，D两人不安排在同一个社区，则不同的分配方法总数为（ ）
A．72B．84C．90D．96
考点四 涂色
【例4】 (2023·浙江·）如图，用五种不同的颜色给图中的O，A，B，C，D，E六个点涂色（五种颜色不一定用完），要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂法种数是（ ）
A．480B．720C．1080D．1200
【举一反三】
1． (2023·山东烟台）我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”.后人称其为“赵爽弦图”.如图，现提供5种颜色给图中的5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同.记事件A：“区域1和区域3颜色不同”，事件B：“所有区域颜色均不相同”，则（ ）
A．B．C．D．
2． (2023·河北·藁城新冀明中学）有4种不同颜色的涂料，给图中的6个区域涂色，要求相邻区域的颜色不相同，则不同的涂色方法共有（ ）
A．1512种B．1346种C．912种D．756种
3 (2023·广东广州）如图，用4种不同的颜色对A，B，C，D四个区域涂色，要求相邻的两个区域不能用同一种颜色，则不同的涂色方法有（ ）
A．24种B．48种C．72种D．96种
6.4 计数原理及排列组合（精讲）（基础版）
思维导图
考点呈现
例题剖析
考点一 排队问题
【例1】 (2023·广东）有7名同学，其中3名男生、4名女生，求在下列不同条件下的排法种数．
(1)选5人排成一排；
(2)全体站成一排，女生互不相邻；
(3)全体站成一排，其中甲不站在最左边，也不站在最右边；
(4)全体站成一排，其中甲不站在最左边，乙不站在最右边；
(5)男生顺序已定，女生顺序不定；
(6)站成三排，前排2名同学，中间排3名同学，后排2名同学，其中甲站在中间排的中间位置；
(7)7名同学站成一排，其中甲、乙相邻，但都不与丙相邻；
(8)7名同学坐圆桌吃饭，其中甲、乙相邻．
【答案】(1)2520(2)144(3)3600(4)3720(5)840(6)720(7)960(8)240
【解析】（1）从7人中选5人排列，排法有（种）．
（2）先排男生，有种排法，再在男生之间及两端的4个空位中排女生，有种排法．故排法共有（种）．
（3）方法一（特殊元素优先法） 先排甲，有5种排法，其余6人有种排法，故排法共有（种）．方法二（特殊位置优先法） 左右两边位置可安排除甲外其余6人中的2人，有种排法，其他位置有种排法，故排法共有（种）．
（4）方法一 分两类：第一类，甲在最右边，有种排法；第二类，甲不在最右边，甲可从除去两端后剩下的5个位置中任选一个，有5种排法，而乙可从除去最右边的位置及甲的位置后剩下的5个位置中任选一个，有5种排法，其余人全排列，有种排法．故排法共有（种）．方法二 7名学生全排列，有种排法，其中甲在最左边时，有种排法，乙在最右边时，有种排法，甲在最左边、乙在最右边都包含了甲在最左边且乙在最右边的情形，有种排法，故排法共有（种）．
（5）7名学生站成一排，有种排法，其中3名男生的排法有种，由于男生顺序已定，女生顺序不定，故排法共有（种）．
（6）把甲放在中间排的中间位置，则问题可以看成剩余6人的全排列，故排法共有（种）．
（7）先把除甲、乙、丙3人外的4人排好，有种排法，由于甲、乙相邻，故再把甲、乙排好，有种排法，最后把排好的甲、乙这个整体与丙分别插入原先排好的4人之间及两端的5个空隙中，有种排法．故排法共有（种）．
（8）将甲、乙看成一个整体，相当于6名同学坐圆桌吃饭，有种排法，甲、乙两人可交换位置，故排法共有（种）．
【一隅三反】
1． (2023·河北·藁城新冀明中学）有名男生和甲、乙名女生排成一排，求下列情况各有多少种不同的排法？
(1)女生甲排在正中间；
(2)名女生不相邻；
(3)女生甲必须排在女生乙的左边（不一定相邻）；
(4)名女生中间恰有名男生．
【答案】(1)种；(2)种；(3)种；(4)种.
【解析】(1)女生甲排在正中间，其余人有种排法，因此不同排法种数为种；
(2)将名男生排成一排，有种排法，2名女生可以在
每2名男生之间及两端共6个位置中选出2个排，有种排法，因此不同排法种数为种；
(3)对7名学生全排列有种排法，因此不同排法种数为种；
(4)选1名男生排在2名女生中间，有种排法，将3人看成1个元素，
与4名男生共5个元素排成一排，不同的排法有种，
又因为2名女生有种排法，因此不同排法种数为种.
2． (2023·全国·高三专题练习）某种产品的加工需要经过道工序．
(1)如果工序不能放在最后，那么有多少种加工顺序？（数字作答）
(2)如果工序必须相邻，那么有多少种加工顺序？（数字作答）
(3)如果工序C，D必须不能相邻，那么有多少种加工顺序？（数字作答）
【答案】(1)96(2)48(3)72
【解析】(1)先从另外4道工序中任选1道工序放在最后，有种不同的排法，再将剩余的4道工序全排列，有种不同的排法，故由分步乘法原理可得，共有种加工顺序；
(2)先排A，B这2道工序，有种不同的排法，再将它们看做一个整体，与剩余的工序全排列，有种不同的排法，故由分步乘法原理可得，共有种加工顺序；
(3)先排其余的3道工序，有种不同的排法，出现4个空位，再将C，D这2道工序插空，有种不同的排法，所以由分步乘法原理可得，共有种加工顺序.
3． (2023·全国·高三专题练习）现有8个人男3女）站成一排.
(1)女生必须排在一起，共有多少种不同的排法？
(2)其中甲必须站在排头有多少种不同排法？
(3)其中甲、乙两人不能排在两端有多少种不同的排法？
(4)其中甲、乙两人不相邻有多少种不同的排法？
(5)其中甲在乙的左边有多少种不同的排法？
(6)其中甲乙丙不能彼此相邻，有多少种不同排法？
(7)男生在一起，女生也在一起，有多少种不同排法？
(8)第3和第6个排男生，有多少种不同排法？
(9)甲乙不能排在前3位，有多少种不同排法？
(10)女生两旁必须有男生，有多少种不同排法？
【答案】(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)
【解析】(1)根据题意，先将3名女生看成一个整体，考虑三人之间的顺序，有种情况，
将这个整体与5名男生全排列，有种情况，则女生必须排在一起的排法有种；
(2)根据题意，甲必须站在排头，有1种情况，将剩下的7人全排列，有种情况，
则甲必须站在排头有种排法；
(3)根据题意，将甲乙两人安排在中间6个位置，有种情况，将剩下的6人全排列，有种情况，
则甲、乙两人不能排在两端有种排法；
(4)根据题意，先将出甲乙之外的6人全排列，有种情况，排好后有7个空位，
则7个空位中，任选2个，安排甲乙二人，有种情况，则甲、乙两人不相邻有种排法；
(5)根据题意，将8人全排列，有种情况，其中甲在乙的左边与甲在乙的右边的情况数目相同，
则甲在乙的左边有种不同的排法；
(6)根据题意，先将出甲乙丙之外的5人全排列，有种情况，排好后有6个空位，
则6个空位中，任选3个，安排甲乙丙三人，有种情况，其中甲乙丙不能彼此相邻有种不同排法；
(7)根据题意，先将3名女生看成一个整体，考虑三人之间的顺序，有种情况，
再将5名男生看成一个整体，考虑5人之间的顺序，有种情况，
将男生、女生整体全排列，有种情况，则男生在一起，女生也在一起，有种不同排法；
(8)根据题意，在5个男生中任选2个，安排在第3和第6个位置，有种情况，
将剩下的6人全排列，有种情况，则第3和第6个排男生，有种不同排法；
(9)根据题意，将甲乙两人安排在后面的5个位置，有种情况，
将剩下的6人全排列，有种情况，甲乙不能排在前3位，有种不同排法；
(10)根据题意，将5名男生全排列，有种情况，排好后除去2端有4个空位可选，
在4个空位中任选3个，安排3名女生，有种情况，则女生两旁必须有男生，有种不同排法.
考点二 排数问题
【例2】 (2023·江苏）用0，1，2，3，4这五个数字组成无重复数字的自然数．
（1）在组成的五位数中，所有奇数的个数有多少?
（2）在组成的五位数中，数字1和3相邻的个数有多少?
（3）在组成的五位数中，若从小到大排列，30124排第几个?
【答案】（1）36个（2）36个（2）49个
【解析】（1）在组成的五位数中，所有奇数的个数有个；
（2）在组成的五位数中，数字1和3相邻的个数有个；
（3）要求在组成的五位数中，要求得从小到大排列，30124排第几个，则计算出比30124小的五位数的情况，比30124小的五位数，则万位为1或2，其余位置任意排，即，故在组成的五位数中比30124小的数有48个，所以在组成的五位数中，若从小到大排列，30124排第49个.
【一隅三反】
1． (2023·吉林）从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数．
试问：（1）能组成多少个不同的五位偶数？
（2）五位数中，两个偶数排在一起的有几个？
（3）两个偶数不相邻且三个奇数也不相邻的五位数有几个？（所有结果均用数值表示）
【答案】（1）576；（2）576；（3）144
【解析】（1）偶数在末尾，五位偶数共有＝576个．
（2）五位数中，偶数排在一起的有＝576个．
（3）两个偶数不相邻且三个奇数也不相邻的五位数有＝144．
2．（2022·全国·高三专题练习）用数字1，2，3，4，5组成没有重复数字的数，问
（1）能够组成多少个五位奇数？
（2）能够组成多少个正整数？
（3）能够组成多少个大于40000的正整数？
【答案】（1）；（2）；（3）；
【解析】（1）首先排最个位数字，从1、3、5中选1个数排在个位有种，其余4个数全排列有种，按照分步乘法计数原理可得有个五位奇数；
（2）根据题意，
若组成一位数，有5种情况，即可以有5个一位数；
若组成两位数，有种情况，即可以有20个两位数；
若组成三位数，有种情况，即可以有60个三位数；
若组成四位数，有种情况，即可以有120个四位数；
若组成五位数，有种情况，即可以有120个五位数；
则可以有个正整数；
（3）根据题意，若组成的数字比40000大的正整数，其首位数字为5或4，有2种情况；
在剩下的4个数，安排在后面四位，共有种情况，
则有个比40000大的正整数；
3． (2023·民大附中海南陵水分校）用0、1、2、3、4五个数字:
(1)可组成多少个五位数；
(2)可组成多少个无重复数字的五位数；
(3)可组成多少个无重复数字的且是3的倍数的三位数；
(4)可组成多少个无重复数字的五位奇数．
【答案】(1)(2)(3)(4)
【解析】(1)
用0、1、2、3、4五个数字组成五位数,相当于从1、2、3、4四个数字中抽取一个放在万位，有种情况，从0、1、2、3、4五个数字中抽取一个放在千位，有种情况，从0、1、2、3、4五个数字中抽取一个放在百位，有种情况，从0、1、2、3、4五个数字中抽取一个放在十位，有种情况，从0、1、2、3、4五个数字中抽取一个放在个位，有种情况，
所以可组成个五位数.
(2)用0、1、2、3、4五个数字组成无重复数字的五位数,相当于先从1、2、3、4四个数字中抽取一个放在万位，有种情况，再把剩下的三个数字和0全排列，有种情况，所以可组成个无重复数字的五位数.
(3)无重复数字的3的倍数的三位数组成它的三个数字之和必须是3的倍数，
所以三个数字必须是0、1、2或0、2、4或1、2、3或2、3、4，
若三个数字是0、1、2，则0不能放在百位，从1和2两个数字中抽取一个放在百位，有种情况，再把剩下的一个数字和0全排列，有种情况；
若三个数字是0、2、4，则0不能放在百位，从2和4两个数字中抽取一个放在百位，有种情况，再把剩下的一个数字和0全排列，有种情况；
若三个数字是1、2、3，则相当于对这三个数字全排列，有种情况;
若三个数字是2、3、4，则相当于对这三个数字全排列，有种情况.
所以根据分类计数原理，共可组成
个无重复数字的且是3的倍数的三位数.
(4)由数字0、1、2、3、4五个数字组成无重复数字的五位奇数，则放在个位的数字只能是奇数，所以放在个位数字只能是1或3，所以相当于先从1、3两个数字中抽取一个放在个位，有种情况，再从剩下的四个数字中除去0抽取一个放在万位，有种情况，再对剩下的三个数字全排列，有种情况，
所以可组成个无重复数字的五位奇数.
考点三 分组分配
【例3】 (2023·全国·高三专题练习）按下列要求分配6本不同的书,各有多少种不同的分配方式?
（1）分成三份,1份1本,1份2本,1份3本;
（2）甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
（3）平均分成三份,每份2本;
（4）平均分配给甲、乙、丙三人,每人2本;
（5）分成三份,1份4本,另外两份每份1本;
（6）甲、乙、丙三人中,一人得4本,另外两人每人得1本;
（7）甲得1本,乙得1本,丙得4本.
【答案】（1）60；（2）360；（3）15；（4）90；（5）15；（6）90；（7）30
【解析】（1）无序不均匀分组问题.先选本有种选法;再从余下的本中选本有种选法;最后余下的本全选有种选法.故共有 (种)选法.
（2）有序不均匀分组问题.由于甲、乙、丙是不同三人,在题的基础上,还应考虑再分配,共有.
（3）无序均匀分组问题.先分三步,则应是种选法,但是这里出现了重复.不妨记六本书为,,,,,,若第一步取了,第二步取了,第三步取了,记该种分法为(,,),则种分法中还有(,,),(,,),(,,),(,,),(,,),共有种情况,而这种情况仅是,,的顺序不同,因此只能作为一种分法,故分配方式有.
（4）有序均匀分组问题.在题的基础上再分配给个人,共有分配方式 (种).
（5）无序部分均匀分组问题.共有 (种)分法.
（6）有序部分均匀分组问题.在题的基础上再分配给个人,共有分配方式 (种).
（7）直接分配问题.甲选本有种选法,乙从余下本中选本有种选法,余下本留给丙有种选法,共有 (种)选法.
【一隅三反】
1．（2023·全国·高三专题练习）为宣传城市文化，提高城市知名度，我市某所学校5位同学各自随机从“趵突腾空”、“ 历山览胜”、“明湖汇泊”三个城市推荐词中选择一个，来确定该学校所推荐的景点，则三个推荐词都有人选的概率是（ ）
A．B．C．D．
【答案】A
【解析】5位同学任意选取1个景点的方法数为，
三个推荐词都有人选，可以先把5人分成三组，然后每组选一个，方法数为，
所以所求概率为．故选：A．
2． (2023·河北·邢台市南和区第一中学）某研究机构采访了“—带一路”沿线20国的青年，让他们用一个关键词表达对中国的印象，使用频率前12的关键词为高铁，移动支付，网购，共享单车、一带一路、无人机、大熊猫、广场舞、中华美食、长城、京剧、美丽乡村．其中使用频率排前4的关键词“高铁、移动支付、网购、共享单车”也成为了他们眼中的“新四大发明”．若将这12个关键词平均分成3组，且各组都包含“新四大发明”关键词．则不同的分法种数为（ ）
A．1680B．3360C．6720D．10080
【答案】B
【解析】先将4个“新四大发明”分成1，1，2三组，有种不同的分法，
再将余下的8个分成3，3，2三组，有种不同的分法，最后配成三组，所以共有种不同的分法．故选：B.
3． (2023·河北省曲阳县第一高级中学）某地区安排A，B，C，D，E，F六名党员志愿者同志到三个基层社区开展防诈骗宣传活动，每个地区至少安排一人，至多安排三人，且A，B两人安排在同一个社区，C，D两人不安排在同一个社区，则不同的分配方法总数为（ ）
A．72B．84C．90D．96
【答案】B
【解析】第一种分配方式为每个社区各两人，则CE一组，DF一组，或CF一组，DE一组，由2种分组方式，再三组人，三个社区进行排列，则分配方式共有种；
第二种分配方式为一个社区1人，一个社区2人，一个社区3人，
当AB两人一组去一个社区，则剩下的4人，1人为一组，3人为一组，则必有C或D为一组，有种分配方法，再三个社区，三组人，进行排列，有种分配方法；
当AB加上另一人三人去一个社区，若选择的是C或D，则有种选择，再将剩余3人分为两组，有种分配方法，将将三个社区，三组人，进行排列，有种分配方法；
若选择的不是C或D，即从E或F中选择1人和AB一起，有种分配方法，再将CD和剩余的1人共3人分为两组，有2种分配方法，将三个社区，三组人，进行排列，有种分配方法，
综上共有12+12+36+24=84种不同的分配方式故选：B
考点四 涂色
【例4】 (2023·浙江·）如图，用五种不同的颜色给图中的O，A，B，C，D，E六个点涂色（五种颜色不一定用完），要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂法种数是（ ）
A．480B．720C．1080D．1200
【答案】D先给O涂色，有种方法，接着给A涂色，有种方法，接着给B涂色，有种方法，
①若C与A同色，则有1种涂色方法，接着给D涂色，有3种涂色方法，
最后E有2种涂色方法；
②若C与A不同色，则有2种涂色方法，接着给D涂色，
若D与A同色，则有1种涂色方法，最后E有3种涂色方法；
若D与A不同色，则有2种涂色方法，最后E有2种涂色方法.
综上，涂色方法总数为故选：D
【举一反三】
1． (2023·山东烟台）我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”.后人称其为“赵爽弦图”.如图，现提供5种颜色给图中的5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同.记事件A：“区域1和区域3颜色不同”，事件B：“所有区域颜色均不相同”，则（ ）
A．B．C．D．
【答案】B
【解析】A事件有 个基本事件，
B事件有 个基本事件，
；
故选：B.
2． (2023·河北·藁城新冀明中学）有4种不同颜色的涂料，给图中的6个区域涂色，要求相邻区域的颜色不相同，则不同的涂色方法共有（ ）
A．1512种B．1346种C．912种D．756种
【答案】D
【解析】1、先涂A区域，则有4种方法，若B，D区域涂相同颜色，则有3种方法，C，E，F区域分别有3种方法，共有4×3×3×3×3=324种方法．
2、先涂A区域，则有4种方法，若B，D区域涂不同颜色，则有3×2种方法，则E区域有2种方法，C，F分别有3种方法，共有4×3×2×2×3×3=432种方法．
故不同的涂色方法共有756种．
故选：D
3 (2023·广东广州）如图，用4种不同的颜色对A，B，C，D四个区域涂色，要求相邻的两个区域不能用同一种颜色，则不同的涂色方法有（ ）
A．24种B．48种C．72种D．96种
【答案】B
【解析】按涂色顺序进行分四步：涂A部分时，有4种涂法；涂B部分时，有3种涂法；涂C部分时，有2种涂法；涂D部分时，有2种涂法.
由分步乘法计数原理，得不同的涂色方法共有种.故选：B.