


数学必修 第二册15.3 互斥事件和独立事件集体备课ppt课件
展开甲、乙两人下棋,甲不输的概率是0.6,两人下成平局的概率是0.3.问题:甲获胜的概率是多少?
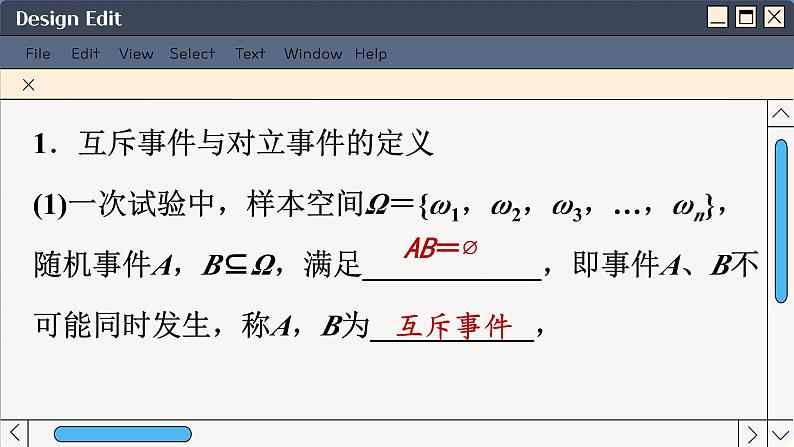
1.互斥事件与对立事件的定义(1)一次试验中,样本空间Ω={ω1,ω2,ω3,…,ωn},随机事件A,B⊆Ω,满足____________,即事件A、B不可能同时发生,称A,B为___________,
如果事件A和事件B互斥,是指事件A和事件B在一次试验中不能同时发生,也就是说,事件A和事件B同时发生的交(和)概率为0,即P(AB)=0.
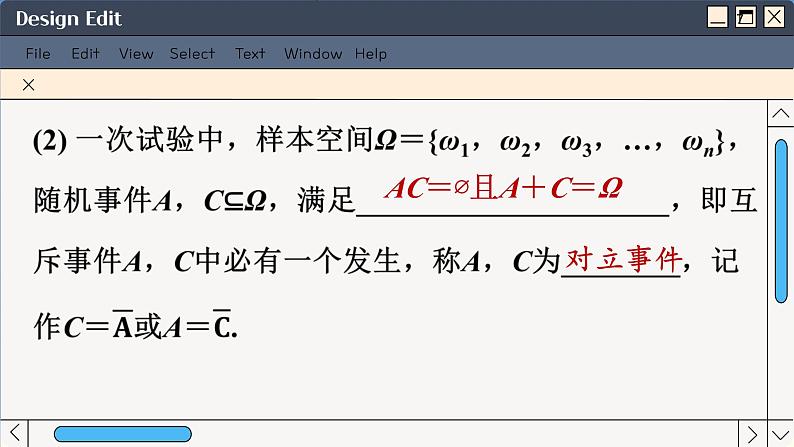
思考:互斥事件与对立事件有什么区别和联系?提示:对立事件一定是互斥事件,互斥事件不一定是对立事件
2.概率加法公式(1)如果事件A,B互斥,那么事件A+B发生的概率,等于事件A,B分别发生的概率的和,即P(A+B)=______________.这就是概率满足的第三个基本性质.
(2)一般地,如果事件A1,A2,…,An中任意两个事件都是互斥事件,那么事件A1,A2,…,An两两互斥.那么P(A1+A2+…+An)=_______________________,即彼此互斥事件和的概率等于每个事件概率的和.
P(A1)+P(A2)+…+P(An)
1.给出以下结论:①互斥事件一定对立;②对立事件一定互斥;③互斥事件不一定对立;④事件A与B的和事件的概率一定大于事件A的概率;⑤事件A与B互斥,则有P(A)=1-P(B).其中正确的命题个数是( )A.2 B.3 C.4 D.5
对立必互斥,互斥不一定对立∴②③正确,①错又当A∪B=A时,P(A∪B)=P(A),∴④错只有A与B为对立事件时,才有P(A)=1-P(B)∴⑤错
2.甲、乙两人下棋,甲获胜的概率是40%,甲不输的概率为90%,则甲、乙两人下成和棋的概率为________.甲不输棋包含甲获胜或甲、乙两人下成和棋,则甲、乙两人下成和棋的概率为90%-40%=50%
互斥事件与对立事件的判断
【例1】 某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.判断下列每对事件是不是互斥事件,如果是,再判断它们是不是对立事件.(1)“恰有1名男生”与“恰有2名男生”;(2)“至少有1名男生”与“全是男生”;
(1)“恰有1名男生”与“恰有2名男生”;因为“恰有1名男生”与“恰有2名男生”不可能同时发生,所以它们是互斥事件.当恰有2名女生时它们都不发生,所以它们不是对立事件.
(2)“至少有1名男生”与“全是男生”;因为恰有2名男生时“至少有1名男生”与“全是男生”同时发生,所以它们不是互斥事件.
(3)“至少有1名男生”与“全是女生”;因为“至少有1名男生”与“全是女生”不可能同时发生,所以它们是互斥事件.由于它们必有一个发生,所以它们是对立事件.
(4)“至少有1名男生”与“至少有1名女生”.当选出的是1名男生、1名女生时,“至少有1名男生”与“至少有1名女生”同时发生,所以它们不是互斥事件.
1.要判断两个事件是不是互斥事件,只需要分别找出各个事件包含的所有结果,看它们之间能不能同时发生.在互斥的前提下,看两个事件的并事件是否为必然事件,从而可判断是否为对立事件.
2.考虑事件的结果间是否有交事件,可考虑利用Venn图分析,对于较难判断的关系,也可考虑列出全部结果,再进行分析.
1.从40张扑克牌(红桃、黑桃、方块、梅花,点数从1~10各10张)中,任取一张.(1)“抽出红桃”与“抽出黑桃”;是互斥事件,不是对立事件.理由是:从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.也不能保证其中必有一个发生,还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.
(2)“抽出红色牌”与“抽出黑色牌”;既是互斥事件,又是对立事件.理由是:从40张扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑色牌”,两个事件不可能同时发生,但其中必有一个发生,所以它们既是互斥事件,又是对立事件.
(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.判断上面给出的每对事件是否为互斥事件,是否为对立事件,并说明理由.不是互斥事件,当然不可能是对立事件.理由是:从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得牌点数为10,因此,二者不是互斥事件,当然不可能是对立事件.
2.某城市有甲、乙两种报纸供居民们订阅,记事件A:“只订甲报”,事件B:“至少订一种报”,事件C:“至多订一种报”,事件D:“不订甲报”,事件E:“一种报也不订”.判断下列每对事件是不是互斥事件,如果是,再判断它们是不是对立事件.(1)A与C;(2)B与E;(3)B与D;(4)B与C;(5)C与E.
(1)A与C由于事件C“至多订一种报”中有可能“只订甲报”,事件A与C有可能同时发生,故A与C不是互斥事件.(2)B与E事件B“至少订一种报”与事件E“一种报也不订”是不可能同时发生的,故B与E是互斥事件,又由于事件B与E必有一个发生,故B与E是对立事件.
(3)B与D事件B“至少订一种报”中有可能只订乙报,即有可能不订甲报,从而事件B与D有可能同时发生,故B与D不是互斥事件.
(4)B与C事件B“至少订一种报”中有这些可能:“只订甲报”“只订乙报”“订甲、乙两种报”.事件C“至多订一种报”中有这些可能:“一种报也不订”“只订甲报”“只订乙报”.由于这两个事件可能同时发生,故B与C不是互斥事件.
(5)C与E.由(4)知,事件E“一种报也不订”只是事件C的一种可能,故C与E有可能同时发生,故C与E不是互斥事件.
【例2】 某一时期内,一条河流某处的年最高水位在各个范围内的概率如下:
计算在同一时期内,河流此处的年最高水位在下列范围内的概率:(1)[10,18];记此处河流的年最高水位在[8,10),[10,12),[12,14),[14,16),[16,18]范围内分别为事件A,B,C,D,E,则这5个事件是彼此互斥的,由互斥事件的概率加法公式
可得:此处河流的年最高水位在[10,18]的概率是P(B+C+D+E)=P(B)+P(C)+P(D)+P(E)=0.90.
(2)[8,14).此处河流的年最高水位在[8,14)的概率是P(A+B+C)=P(A)+P(B)+P(C)=0.76.
1.将一个事件拆分为若干个互斥事件,分别求出各事件的概率,然后用加法公式计算结果.2.在运用互斥事件的概率加法公式解题时,首先要分清事件间是否互斥,同时要会把一个事件拆分成几个互斥事件,做到不重不漏.
3.常用步骤:(1)确定诸事件彼此互斥;(2)诸事件中有一个发生;(3)先求诸事件分别发生的概率,再求和.
4.某家庭电话在家中有人时,打进的电话响第1声时被接的概率为0.1,响第2声时被接的概率为0.3,响第3声时被接的概率为0.4,响第4声时被接的概率为0.1,那么电话在响前4声内被接的概率是多少?[解] 记“响第1声时被接”为事件A,“响第2声时被接”为事件B,“响第3声时被接”为事件C,“响第4声时被接”为事件D,“响前4声内被接”为事件E,
则易知A,B,C,D互斥,且E=A+B+C+D,所以由互斥事件的概率加法公式,得P(E)=P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)=0.1+0.3+0.4+0.1=0.9.
【例3】 一个袋中装有4个形状、大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取2个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取1个球,该球的编号为m,将球放回袋中,再从袋中随机取1个球,该球的编号为n,求n
6.玻璃球盒中装有各色球12只,其中5红、4黑、2白、1绿,从中任取1球,求:(1)得到红球或黑球的概率;记事件A1:从12只球中任取1球得红球;A2:从12只球中任取1球得黑球;A3:从12只球中任取1球得白球;A4:从12只球中任取1球得绿球,
【例4】 抛掷一个均匀的正方体玩具(各个面上分别有1,2,3, 4,5,6这6个数字),求:(1)落地时向上的数是偶数的概率;列表如下:
“互斥”和“对立”都是针对两个事件而言.“互斥”是指两个事件不能同时发生;“对立”是指两个互斥事件有且仅有一个发生.对于求复杂事件的概率通常有两种方法:一是将所求事件转化为彼此互斥的事件的和;二是先求出所求事件的对立事件的概率,进而再求所求事件的概率.
7.掷一枚骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则事件A+发生的概率为 .
1.本节课的重点是理解互斥事件和对立事件的概念及关系难点是利用互斥事件、对立事件间的概率关系求事件发生的概率.
2.应用互斥事件的概率的加法公式解题时,首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求对立事件的概率.
1.从1,2,…,9中任取两数,其中: ①恰有一个偶数和恰有一个奇数;②至少有一个奇数和两个数都是奇数;③至少有一个奇数和两个数都是偶数;④至少有一个奇数和至少有一个偶数.在上述事件中,为对立事件的是( )A.① B.②④ C.③ D.①③
从1,2,…,9中任取两数,包括一奇一偶、两奇、两偶,共三种互斥事件,所以只有③中的两个事件才是对立事件.
3张奖券只有1张能中奖,3名同学有放回地抽取.事件A为“第一名同学没有抽到中奖奖券”,事件B为“第三名同学抽到中奖奖券”.问题:上述问题中事件A的发生是否会影响B发生的概率?事件A和事件B相互独立吗?
1.相互独立事件的概念一般地,如果事件A是否发生______事件B发生的概率,那么称A、B为相互独立事件.
2.相互独立事件的概率计算(1)两个事件A,B相互独立的充要条件是_______________.(2)若事件A1,A2,…,An相互独立,那么这n个事件同时发生的概率P(A1A2…An)=P(A1)P(A2)…P(An).
P(AB)=P(A)P(B)
思考1:不可能事件与任何一个事件相互独立吗?相互独立.不可能事件的发生与任何一个事件的发生没有影响.
思考2:必然事件与任何一个事件相互独立吗?相互独立.必然事件的发生与任何一个事件的发生没有影响.
3.甲,乙,丙三人将参加某项测试,他们能达标的概率分别是0.8,0.6,0.5,则三人都达标的概率是________,三人中至少有一人达标的概率是________.三人都达标的概率为0.8×0.6×0.5=0.24.三人都不达标的概率为(1-0.8)×(1-0.6)×(1-0.5)=0.2×0.4×0.5=0.04.三人中至少有一人达标的概率为1-0.04=0.96
【例1】 判断下列各对事件是否是相互独立事件.(1)甲组3名男生,2名女生,乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,“从甲组中选出1名男生”与“从乙组中选出1名女生”;
[解] (1)“从甲组中选出1名男生”这一事件是否发生,对“从乙组中选出1名女生”这一事件发生的概率没有影响,所以它们是相互独立事件.
判断事件是否相互独立的方法(1)定义法:事件A,B相互独立⇔P(AB)=P(A)·P(B).(2)由事件本身的性质直接判定两个事件发生是否相互影响.
[跟进训练]1.同时掷两颗质地均匀的骰子,令A={第一颗骰子出现奇数点},令B={第二颗骰子出现偶数点},判断事件A与B是否相互独立.[解] 样本空间Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),
(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},A={第一颗骰子出现1,3,5点}={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)},
相互独立事件发生的概率
(2)他们都失败的概率;
(3)他们能够研制出疫苗的概率.“他们能研制出疫苗”的对立事件为“他们都失败”,结合对立事件间的概率关系可得所求事件的概率
1.求相互独立事件同时发生的概率的步骤(1)首先确定各事件之间是相互独立的;(2)确定这些事件可以同时发生;(3)求出每个事件的概率,再求积.
2.使用相互独立事件同时发生的概率计算公式时,要掌握公式的适用条件,即各个事件是相互独立的,而且它们能同时发生.
2.一个袋子中有3个白球,2个红球,每次从中任取2个球,取出后再放回,求:(1)第1次取出的2个球都是白球,第2次取出的2个球都是红球的概率;记“第1次取出的2个球都是白球”的事件为A,“第2次取出的2个球都是红球”的事件为B,“第1次取出的2个球中1个是白球、1个是红球”的事件为C,很明显,由于每次取出后再放回,A,B,C都是相互独立事件.
(2)第1次取出的2个球中1个是白球、1个是红球,第2次取出的2个球都是白球的概率.
事件的相互独立性与互斥性
3.由探究1、2,你能归纳出相互独立事件与互斥事件的区别吗?
【例3】 红队队员甲、乙、丙与蓝队队员A,B,C进行围棋比赛,甲对A、乙对B、丙对C各一盘.已知甲胜A、乙胜B、丙胜C的概率分别为0.6,0.5,0.5.假设各盘比赛结果相互独立.求:
(2)求红队至少两名队员获胜的概率.
1.本题(2)中用到直接法和间接法.当遇到“至少”“至多”问题可以考虑间接法.2.求复杂事件的概率一般可分三步进行:(1)列出题中涉及的各个事件,并用适当的符号表示它们;
(2)理清各事件之间的关系,恰当地用事件间的“并”“交”表示所求事件;(3)根据事件之间的关系准确地运用概率公式进行计算.
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)出现几人合格的概率最大.
1.本节课的重点是事件的相互独立性及其概率的求法,难点是事件相互独立性的判断.2.要掌握事件相互独立性的两个问题.(1)事件相互独立性的判断.(2)事件相互独立性概率的求法.
3.求复杂事件概率的步骤:(1)列出题中涉及的各种事件,并用适当的符号表示;(2)理清事件之间的关系(两事件是互斥、对立,还是相互独立),列出关系式;
(3)根据事件之间的关系准确选取概率公式进行计算;(4)当直接计算符合条件的事件的概率较复杂时,可先间接地计算对立事件的概率,再求出符合条件的事件的概率.
2.抛掷3枚质地均匀的硬币,A={既有正面向上又有反面向上},B={至多有一个反面向上},则A与B的关系是( )A.互斥事件 B.对立事件C.相互独立事件 D.不相互独立事件由于事件A的发生与否对于事件B的发生不产生影响,则事件A与事件B相互独立,故选C.
苏教版 (2019)必修 第二册15.3 互斥事件和独立事件课文课件ppt: 这是一份苏教版 (2019)必修 第二册15.3 互斥事件和独立事件课文课件ppt,文件包含苏教版高中数学必修第二册第15章153第2课时独立事件课件ppt、苏教版高中数学必修第二册第15章153第2课时独立事件学案doc、苏教版高中数学必修第二册课后素养落实47独立事件含答案doc等3份课件配套教学资源,其中PPT共58页, 欢迎下载使用。
苏教版 (2019)必修 第二册第15章 概率15.3 互斥事件和独立事件教学演示课件ppt: 这是一份苏教版 (2019)必修 第二册第15章 概率15.3 互斥事件和独立事件教学演示课件ppt,共51页。PPT课件主要包含了基础认知·自主学习,学情诊断·课时测评等内容,欢迎下载使用。
苏教版 (2019)必修 第二册15.3 互斥事件和独立事件课前预习ppt课件: 这是一份苏教版 (2019)必修 第二册15.3 互斥事件和独立事件课前预习ppt课件,共47页。PPT课件主要包含了基础认知·自主学习,不可能同时,学情诊断·课时测评等内容,欢迎下载使用。













