沪科版九年级数学下册 第24章 圆 第1课时 旋转、旋转对称图形（课件）

这是一份沪科版九年级数学下册 第24章 圆 第1课时 旋转、旋转对称图形（课件），共26页。
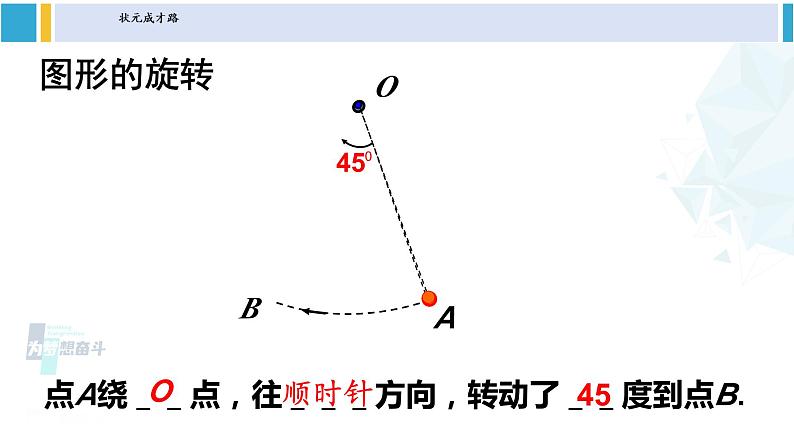
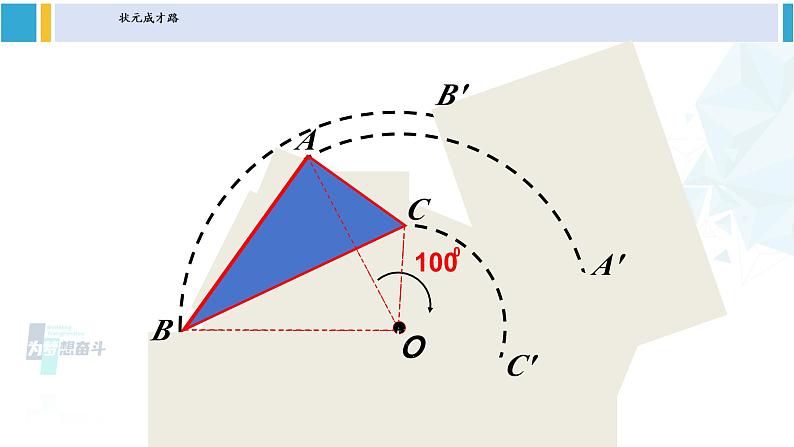
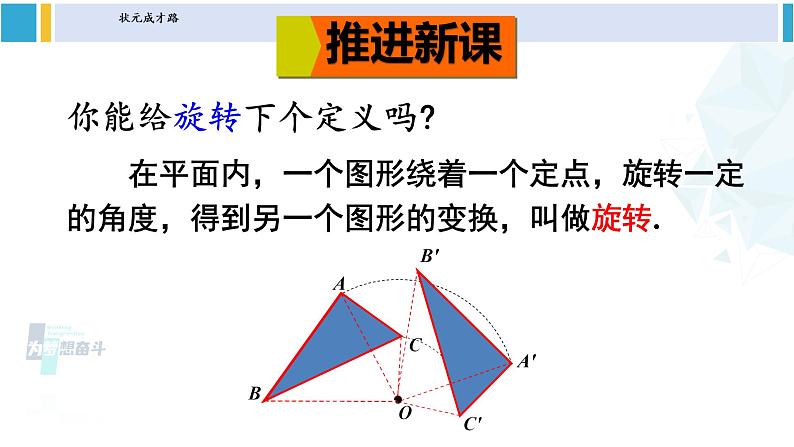
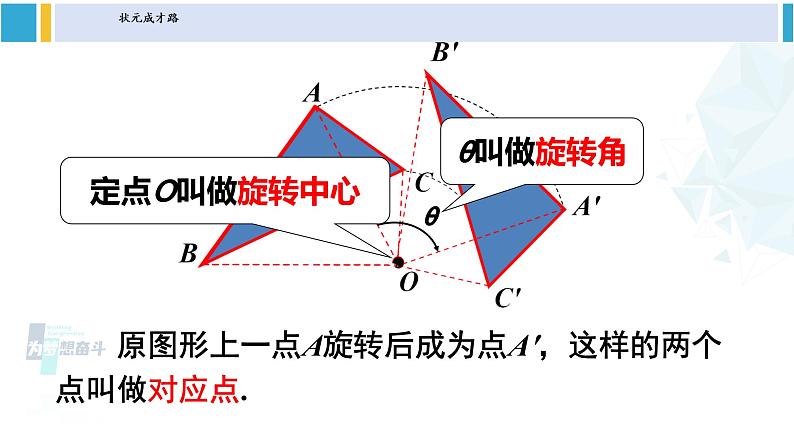
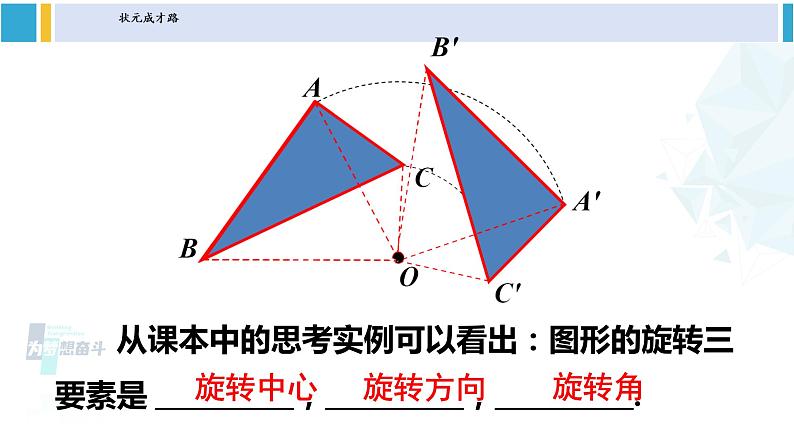
第24章 圆24.1 旋转第1课时 旋转、旋转对称图形沪科版九年级下册思 考：这些运动有什么共同的特征？图形的旋转BOA点A绕＿＿点，往＿＿＿方向，转动了＿＿度到点B.O顺时针45OBABAB′A′OCC′ 在平面内，一个图形绕着一个定点，旋转一定的角度，得到另一个图形的变换，叫做旋转.你能给旋转下个定义吗?θ 原图形上一点A旋转后成为点A′，这样的两个点叫做对应点.定点O叫做旋转中心θ叫做旋转角 从课本中的思考实例可以看出：图形的旋转三要素是 ， ， .旋转中心旋转方向旋转角试一试如图，△ABO绕点O旋转得到△CDO，则:点B的对应点是_____________.线段OB的对应线段是_____________.线段CD的对应线段是_____________.∠AOB的对应角是_____________.∠B的对应角是_____________.旋转中心是_____________.点D线段OD线段AB∠COD∠D点O 旋转中心就是在旋转过程中始终保持固定不变的那个点，它可以在图形的外部或内部，还可以在图形上，即它可以是平面内的任意一点. 旋转角：任意一对对应点与旋转中心的连线所成的角. ①时钟的时针在不停地旋转，从上午6时到上午9时，时针旋转的角度是多少？从上午9时到上午10时呢？ 解：从上午6时到上午9时，时针旋转的角度为90°，从上午9时到上午10时，时针旋转的角度是30°.练习 ②如图，杠杆绕支点转动撬起重物，杠杆的旋转中心是点 ，旋转角是 ，点A的对应点是点 ．O∠AOA′A′观察 如图，△ABC绕着旋转中心O按逆时针方向旋转θ后，得到△A′B′C′.①OA与OA′、OB与OB′、OC与OC′分别有何关系？ .②∠AOA′、∠BOB′、∠COC′之间有何关系？ .③△ABC与△A′B′C′有何关系？ .分别相等∠AOA′=∠BOB′=∠COC′△ABC≌△A′B′C′ 在一个图形和它经过旋转所得到的图形中，对应点到旋转中心的距离相等；两组对应点分别与旋转中心的连线所成的角相等，都等于旋转角；旋转中心是唯一不动的点.归纳小结◆旋转前、后的图形全等. ◆对应点到旋转中心的距离相等. ◆每一对对应点与旋转中心的连线所成的角彼此相等. ◆图形的旋转是由旋转中心和旋转的角度决定. 旋转的基本性质思 考：这些图形有什么共同特征？ 在平面内，一个图形绕着一个定点旋转一定的角度θ（0°＜θ＜360°）后，能够与原图形重合，这样的图形叫做旋转对称图形.BACO 一个图形绕着一个定点，按照一定的角度，从一个位置旋转到另一个位置，叫做旋转.ABCO· 一个图形绕着一个定点，旋转一定的角度后能与自身重合，这样的图形称为旋转对称图形.图形的一种变换图形的一种特性　　思考：香港特别行政区区徽可以看作是什么“基本图案”通过怎样的旋转而得到的？　　可以看作是一个花瓣连续4次旋转所形成的，每次旋转分别等于72°1. 下列现象中属于旋转的有（ ）①火车行驶；②荡秋千运动；③方向盘的转动；④钟摆的运动；⑤圆规画圆．A．1个 B．2个 C．3个 D．4个D2. 把图中的五角星图案，绕着它的中心点O旋转，旋转角为多少度时，旋转后的五角星能与自身重合？解：旋转角为72°或144°或216°或288°时， 旋转后的五角星能与自身重合.3. 如图，△ABD、△AEC都是等边三角形，BE与DC有什么关系？你能用旋转的性质说明上述关系成立的理由吗？解：BE=DC.理由：将△ABE顺时针绕点A顺时针旋转60°就能和△ACD重合. 即△ADC≌△ABE，所以BE=DC. 旋转前后两个图形的形状、大小不变，因此我们在用旋转解决与其相关的问题时要注意： ①明确旋转中的“变”与“不变”； ②明确旋转前后的对应关系； ③明确旋转过程中线段或角之间的关系.1.从课后习题中选取；2.完成练习册本课时的习题。