辽宁省抚顺市清原县2024届九年级上学期期末质量检测数学试卷(含答案)

这是一份辽宁省抚顺市清原县2024届九年级上学期期末质量检测数学试卷(含答案)，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下列航天图标中，是中心对称图形的是( )
A.B.C.D.
2．下列事件中，属于必然事件的是( )
A.任意购买一张电影票，座位号是奇数
B.五个人分成四组，这四组中有一组必有两人
C.抛一枚质地均匀的硬币，正面朝上
D.打开手机就有未接电话
3．一元二次方程的根的情况为( )
A.有两个不相等的实数根B.没有实数根
C.有两个相等的实数根D.只有一个实数根
4．设，，是抛物线上的三点，则，，的大小关系为( )
A.B.C.D.
5．如图，在一个圆形转盘中，标有黄、红、绿的三个扇形的圆心角度数分别为、、.让转盘自由转动，转盘停止后指针（若指针落在分界线上，则重新转动转盘）落在红扇形的概率是( )
A.B.C.D.
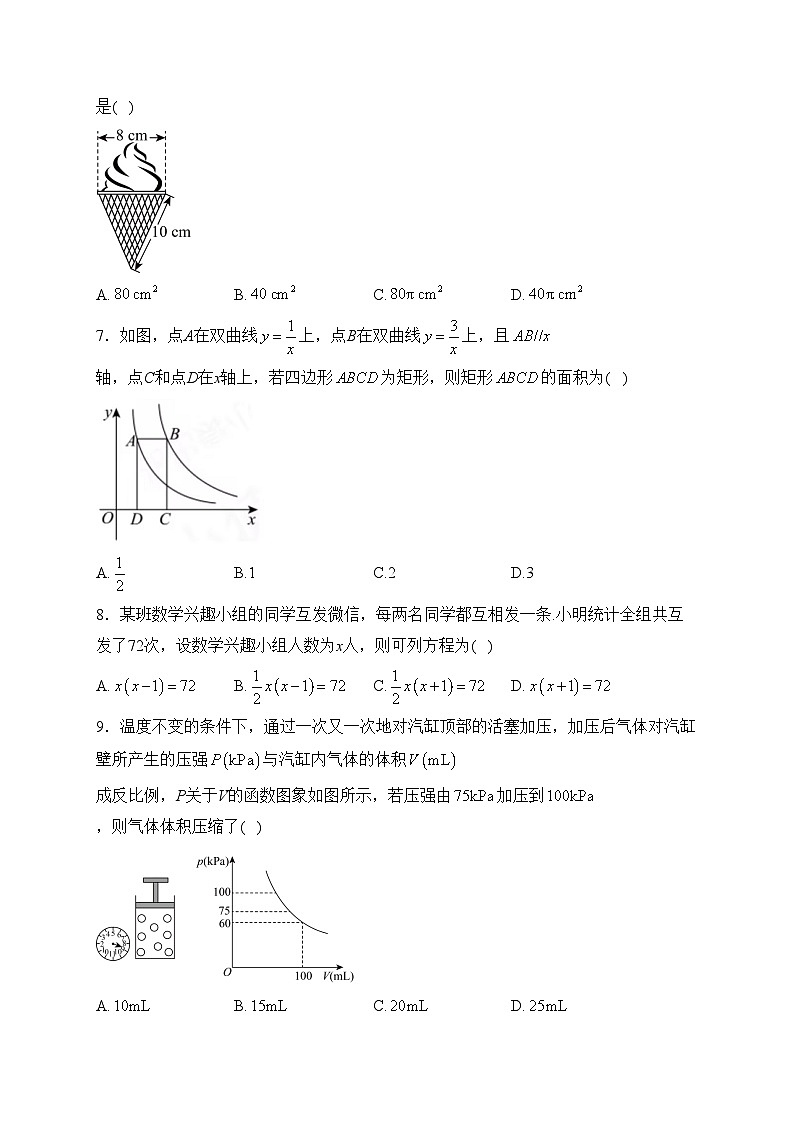
6．如图，冰激凌蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积（接缝忽略不计）是( )
A.B.C.D.
7．如图，点A在双曲线上，点B在双曲线上，且轴，点C和点D在x轴上，若四边形为矩形，则矩形的面积为( )
A.B.1C.2D.3
8．某班数学兴趣小组的同学互发微信，每两名同学都互相发一条.小明统计全组共互发了72次，设数学兴趣小组人数为x人，则可列方程为( )
A.B.C.D.
9．温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，加压后气体对汽缸壁所产生的压强与汽缸内气体的体积成反比例，P关于V的函数图象如图所示，若压强由加压到，则气体体积压缩了( )
A.B.C.D.
10．如图，已知中，，将绕点A沿逆时针方向旋转得到，交于点F，交、于点G、H，则以下结论：
①；
②连接、，则；
③当时，的长度最大；
④当点H是的中点时，四边形的面积等于.
其中正确的个数有( )
A.1个B.2个C.3个D.4个
二、填空题
11．若是关于x的一元二次方程的一个根，则m的值为________.
12．一个小球在如图所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大小、质地完全相同，那么该小球停留在黑色区域的概率是______.
13．如图1，A，B表示某游乐场摩天轮上的两个轿厢，如图2是其示意图，点O是圆心，半径r为，点A，B是圆上的两点，圆心角，则的长为______m.（结果保留）
14．如图，矩形的顶点O在坐标原点，顶点B，C分别在x轴，y轴上，顶点A在反比例函数（k为常数，，）的图象上，，将矩形ABOC绕点A按逆时针方向旋得到矩形.若点O的对应点恰好落在此反比例函数图象上，则k的值为______.
15．如图，在四边形ABCD中，，，，，，含角的直角三角板EMN的顶点E在边BC上移动，，直角边ME始终经过点A，斜边EN与CD交于点F.当是以AB为腰的等腰三角形时，线段CF长度的最大值等于_________.
三、解答题
16．解方程：
（1）；
（2）.
17．如图，在正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，的三个顶点坐标分别为，，.
（1）画出与关于原点中心对称的图像；
（2）画出绕点顺时针旋转后得到；
（3）观察图形，判断能否由旋转得到？如果能，请直接写出旋转中心，如果不能，请说明理由.
18．某社会实践活动小组为了了解“本校学生上学和放学交通方式”的情况，在全校三个年级中随机抽取了部分同学发放了调查问卷，设计的问卷如下
请根据以上信息解答下列问题：
（1）求被随机抽取的人数是多少？并补全条形统计图；
（2）若该校共有学生1500人，估计该校步行上下学的人数.
（3）太原市“共享出行家庭"又添新伙伴，f单车入驻龙城.目前太原市共有4种公共单车供市民租借，分别是公共自行车、酷骑单车、百拜单车、f单车.小聪和小明放学常乘共享单车.今天他俩从“公共自行车、酷骑单车、百拜单车、f”四种共享单车中随机选择一种骑行回家（每一种单车都有可能被选中）.用树状图或列表的方法，求两人都选择同一种单车回家的概率.（“公共自行车、酷骑单车、百拜单车、f”分别用字母“G”，“K”、“B”和“O”表示）
19．如图，点A的坐标是，点B的坐标是，点C为中点，将绕着点B逆时针旋转得到.
（1）反比例函数的图像经过点，求该反比例函数的表达式；
（2）一次函数图像经过A、两点，求该一次函数的表达式.
20．某市政府大力扶持大学生创业，李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现，如果以单价26元销售，那么一个月内可售出240台.根据销售经验，提高销售单价会导致销售量减少，即销售单价每提高1元，销售量相应减少10台.根据物价部门规定，这种护眼台灯的销售单价不得低于进价且不得高于32元.
（1）求每月销售量y（件）与销售单价x（元）之间的函数关系式；
（2）设李明每月获得利润为w（元），当销售单价定为多少元时每月可获得最大利润，每月最大利润是多少？
21．如图，，为的直径，C为上一点，过点C的切线与的延长线交于点P，，点E是的中点，弦，相交于点E.
（1）求的度数；
（2）若，求直径的长.
22．综合与实践
问题情境
数学课上，老师出示这样一道题：如图，正方形的边长为12，点E在上，，连接，以为边作正方形.
操作发现
（1）如图1，连接，直接写出线段的长；
操作探究
（2）如图2、在边上截取，连接，，判断四边形的形状，并说明理由；
拓展探究
（3）如图3，把正方形绕点A顺时针旋转，点E落在正方形内部，连接，，作的边的中线，发现，，请证明.
23．综合与探究：如图，二次函数的图象与x轴交于，两点，与y轴交于点C，连接，，P为抛物线上的一个动点（与点A、B、C不重合），设点P的横坐标为m，的面积为S.
（1）求二次函数的表达式；
（2）当点P在第二象限内时，求S关于m的函数表达式；
（3）抛物线上是否存在点P，使？若存在，请直接写出点P的坐标；若不存在，请说明理由.
参考答案
1．答案：A
解析：A、是中心对称图形，故符合题意；
B、不是中心对称图形，故不符合题意；
C、不是中心对称图形，故不符合题意；
D、不是中心对称图形，故不符合题意；
故选：A.
2．答案：B
解析：A、任意购买一张电影票，座位号不一定是奇数，不是必然事件，不符合题意；
B、五个人分成四组，这四组中有一组必有两人，是必然事件，符合题意；
C、抛一枚质地均匀的硬币，正面不一定朝上，不是必然事件，不符合题意；
D、打开手机就不一定有未接电话，不是必然事件，不符合题意；
故选B.
3．答案：B
解析：，
该方程没有实数根.
故选B.
4．答案：A
解析：抛物线的开口向下，对称轴为直线，
，
.
故选：A.
5．答案：B
解析：指针落在红色区域的概率.
故选：B.
6．答案：D
解析：由图知，底面直径为8，母线长为10，
则底面周长为，，
所以蛋筒圆锥部分包装纸的面积是，.
故选：D.
7．答案：C
解析：四边形为矩形，
点A与点B纵坐标相等，点A与点D横坐标相等，
又点A在双曲线上，点B在双曲线上
设，，，
则用坐标之差表示：
，，
.
故选：C.
8．答案：A
解析：由题意得，，
故选：A.
9．答案：C
解析：设P关于V的函数解析式为，由图象可把点代入得：，
P关于V的函数解析式为，
当时，则，
当时，则，
压强由加压到，则气体体积压缩了；
故选：C.
10．答案：D
解析：①，
，
由旋转得，，，
，故①正确；
②连接、，
，
，，
，，
，
，
，
又，
，
，
垂直平分FH，故②正确；
③，AD是定长，
最小时，DF最长，
时，DF的长度最大，故③正确；
④，
当点H是DE的中点时，有，
，，，
，
，故④正确.
故选：D.
11．答案：5
解析：把代入方程 ，
得，
解得.
故答案为：5.
12．答案：
解析：根据题意可得：图中共有10块大小相同的小方格地砖，其中黑色区域的面积恰好等于5块小方格地砖的面积，
所以该小球停留在黑色区域的概率；
故答案为：.
13．答案：
解析：，半径r为，
的长.
故答案为：.
14．答案：
解析：设则，，
根据反比函数k的几何意义可得：，
即，
解得：，
A，两点在第一象限，
，
A的坐标为，
A点在反比例函数图像上，
.
15．答案：
解析：如图，过点A、D分别作的垂线，垂足分别为G、H，
则，，
，
四边形为矩形，
，；
，，
；
，，
，
，，
，，
，
，
由勾股定理得：；
①如图，当时，则，
，
，
即，
；
；
②当时，如图，
此时，
；
，
，
即，
，
，
，
由勾股定理得：；
，
线段长度的最大值等于；
故答案为：.
16．答案：（1），
（2），
解析：（1），
，
，
即，
，
，；
（2）
，，，
，
，
，.
17．答案：（1）见解析
（2）见解析
（3）能由旋转得到，旋转中心为
解析：（1）如图1所示：即为所求；
（2）如图2所示：即为所求；
（3）如图3，能由旋转得到，旋转中心为.
18．答案：（1）200人，见解析
（2）405人
（3）见解析，
解析：（1）抽取总人数：（人），
选择“公交”人数：（人），
补全条形统计图如图所示：
（2）（人）；
答：该校步行上下学的人数为405人；
（3）画出树状图如图所示：
由图知，四种共享单车中随机选择一种，一共有16种情况，且每种情况出现的可能性相同，两人都选择同一种单车回家的情况有4种，
.
19．答案：（1）
（2）
解析：（1）点B的坐标是，点C为中点，
，，
由旋转可得：，，
，
，
反比例函数的表达式为；
（2）如图，过作于H，
则，而，，
，
，
，
，，
，
，
设直线为，
，解得：，
直线为.
20．答案：（1）
（2）当销售单价定为32元时，每月可获得最大利润；每月获得最大利润为2160元
解析：（1）由题意得：，
每月销售量y（件）与销售单价x（元）之间的函数关系式；
（2）由题意，得：
，
，
，，
时，，
答：当销售单价定为32元时，每月可获得最大利润；每月获得最大利润为2160元.
21．答案：（1）
（2）
解析：（1）与相切于点C，
，
，
，
，
，
，
，即，
，
；
（2）如图，连接，
是直径，
，
点E是的中点，
，
，
在中，
，，
，
在中，
，
，
的直径的长为.
22．答案：（1）
（2）四边形为平行四边形，理由见解析
（3）见解析
解析：（1）过点G作垂直于的延长线交于点H，则，
四边形是正方形，
，，，
则，
又四边形是正方形，
，，
则，
，
，
，，则，
；
（2）四边形为平行四边形，理由如下：
四边形是正方形，
，，则，
又四边形是正方形，
，，则，
，
又，
，
，，
，
四边形为平行四边形；
（3）连接并延长，使得，连接，则，
是的中线，
，
又，
，
，，
，
，
，
。
则
，
，
又，
，
，，
，
，
，
，
.
23．答案：（1）
（2）
（3）存在；或
解析：（1）二次函数的图象与x轴交于、两点，
，
，
二次函数的表达式为数；
（2）过点P作轴于点N，如图，
则，
令，则，
，
，
，
，
点P的横坐标为m，
，
点P在第二象限内，
，，
，，
，
，
S关于m的函数表达式为：；
（3）①当点P在上方时，如图，
，
，
点，的纵坐标相等，
点的纵坐标为，
令，则，
解得：或，
；
②当点P在下方时，如图，
设交x轴于点H，
，
，
设，
，
在中，
，
，
解得：，
，
，
设直线的解析式为，
，
解得：，
直线的解析式为，
联立，
解得：，，
，
综上所述，点P的坐标为或.
问卷调查
请你选择上学和放学最常采用的一种交通方式，并勾选出来.
A.私家车
B.公交
C.出租车
D.共享单车
E.步行