宁夏回族自治区银川市银川阅海中学2023-2024学年七年级上学期期中数学试题（原卷+解析）

这是一份宁夏回族自治区银川市银川阅海中学2023-2024学年七年级上学期期中数学试题（原卷+解析），文件包含精品解析宁夏回族自治区银川市银川阅海中学2023-2024学年七年级上学期期中数学试题原卷版docx、精品解析宁夏回族自治区银川市银川阅海中学2023-2024学年七年级上学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

（本试卷满分120分）
（注：班级、姓名、学号、座位号一律写在装订线以外规定的地方，卷面不得出现任何标记．）
一、选择题（每题3分，共24分）
1. 下列几何体中，面数最少的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】弄清每个几何体的面数即可．
【详解】解：球有1个面，圆柱有3个面，圆锥有2个面，正方体有6个面，面数最少的是球．
故选：A．
【点睛】本题考查几何体的组成，几何体是由面围成的，而面又分为平面和曲面．能准确区分平面和曲面是解题的关键．
2. 下列各组数中，相等的是（ ）
A. 2和B. 和
C. 2和D. 和
【答案】C
【解析】
【分析】本题考查的是比较两数，涉及到相反数、绝对值等知识点，熟练掌握相反数、绝对值是解决问题的关键．
【详解】解：A、2和不相等，不符合题意；
B、∵，，
∴和不相等，错误，不符合题意；
C、∵，正确，符合题意；
D、∵，，
∴和不相等，错误，不符合题意．
故选：C．
3. 如图，小明将装有一半水的密闭圆柱形玻璃杯水平放置，此时水面的形状（ ）
A. 圆B. 长方形C. 等腰梯形D. 椭圆
【答案】B
【解析】
【分析】本题考查了截几何体和认识立体图形．根据垂直于圆柱底面的截面是长方形，可得答案．
【详解】解：由水平面与圆柱的底面垂直，得
水面的形状是长方形．
故选：B．
4. 如图，在数轴上，点、分别表示数、，且．若、两点间的距离为，则点表示的数为( )
A. B. 6C. D. 3
【答案】C
【解析】
【分析】根据，结合数轴，即可求解．
【详解】解：∵点、分别表示数、，且，、两点间的距离为，
∴
∴，
故选：C．
【点睛】本题考查了求数轴上两点距离，相反数的意义，数形结合是解题的关键．
5. 下列说法中正确的是（）
A. 绝对值等于它本身的数只有零
B. 最大的负整数是
C. 任何一个有理数都有倒数
D. 有理数分为正有理数和负有理数
【答案】B
【解析】
【分析】根据绝对值的性质，最大负整数，倒数，及有理数分类的有关知识进行作答，即可．
【详解】A. 绝对值等于它本身的数是正数和零，故选项A错误，不符合题意；
B. 最大的负整数是，故选项B正确，符合题意；
C.有理数中零没有倒数，故选项C错误，不符合题意；
D. 有理数分为正有理数、零和负有理数，故选项D错误，不符合题意；
故选B．
【点睛】本题主要考查了有理数的分类，最大负整数，零没有倒数，绝对值的有关知识．
6. 下列判断正确的是（ ）．
A. 与不是同类项B. 不是整式
C. 单项式的系数是D. 是二次三项式
【答案】C
【解析】
【分析】直接利用单项式的系数以及多项式的次数与项数确定方法及多项式命名方式分别分析得出答案；
【详解】选项A：与是同类项，故选项A错误，不符合题意；
选项B：是整式，选项B错误，不符合题意；
选项C：单项式的系数是，选项C正确，符合题意；
选项D：是三次三项式，选项D错误，不符合题意；
故答案为：C.
【点睛】本题主要考查了单项式，多项式的定义，掌握单项式和多项式的定义是解题的关键.
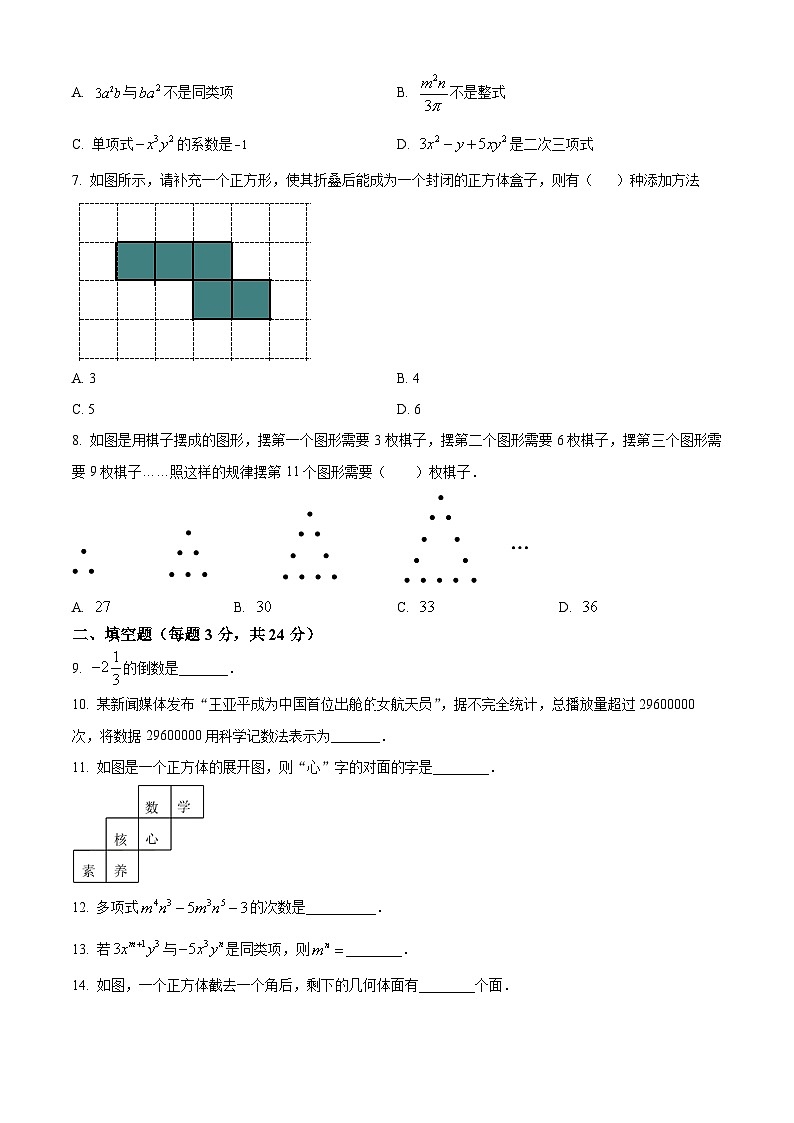
7. 如图所示，请补充一个正方形，使其折叠后能成为一个封闭的正方体盒子，则有（ ）种添加方法
A. 3B. 4
C. 5D. 6
【答案】B
【解析】
【分析】由平面图形的折叠及正方体的展开图解题，正方体共有11种表面展开图，识记正方体展开图的各种情形，即可轻松画图．
【详解】解：共有4种添加方法，
故选：B．
【点睛】此题考查正方体的展开图，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．
8. 如图是用棋子摆成的图形，摆第一个图形需要3枚棋子，摆第二个图形需要6枚棋子，摆第三个图形需要9枚棋子……照这样的规律摆第11个图形需要（ ）枚棋子．

A. B. C. D.
【答案】C
【解析】
【分析】将棋子数适当表示，从中寻找蕴含的基本规律即可．
【详解】解：第一个图案中，棋子总数是；
第二个图案中，棋子总数为；
第三个图案中，棋子总数为；
……
第个图案中，棋子总数有；
所以当时，棋子总数为：（个），
即摆第11个图形需要个棋子．
故选：C．
【点睛】本题考查了整式中的规律探究，根据棋子数从特殊到一般去确定规律是解题的关键．
二、填空题（每题3分，共24分）
9. 的倒数是_______．
【答案】
【解析】
【分析】先将分数化成假分数，根据互为倒数的两数积为，即可求出答案．
【详解】解：，
，
的倒数为，
故答案为：．
【点睛】本题考查了倒数的定义，掌握互为倒数的两数积为是解题关键．
10. 某新闻媒体发布“王亚平成为中国首位出舱的女航天员”，据不完全统计，总播放量超过29600000次，将数据29600000用科学记数法表示为_______．
【答案】2.96×107
【解析】
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【详解】解：29600000＝2.96×107．
故答案为：2.96×107．
【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
11. 如图是一个正方体的展开图，则“心”字的对面的字是________．
【答案】素
【解析】
【分析】本题考查正方体的展开图的特征．根据正方体的展开图的特征进行判断即可．
【详解】解：根据正方体展开图的特征“端首尾是对面”可知，
“心”的对面是“素”，
故答案为：素．
12. 多项式的次数是__________．
【答案】
【解析】
【分析】根据多项式的项的定义，多项式的次数的定义即可确定其次数．
【详解】解：由于组成该多项式的单项式（项）共有三个，，，
其中最高次数为，
所以多项式的次数是．
故答案为：．
【点睛】本题考查了对多项式的项和次数的掌握情况，难度不大．解题的关键是明确多项式的次数是多项式中最高次项的次数．
13. 若与是同类项，则________．
【答案】8
【解析】
【分析】本题考查了同类项的定义．根据同类项的定义得出，，求出，的值，再代入求出答案即可．
【详解】解：与是同类项，
，，
，
．
故答案为：8．
14. 如图，一个正方体截去一个角后，剩下的几何体面有________个面．
【答案】7
【解析】
【分析】本题考查了立体图形的认识，截面的形状．观察图形，数剩下的几何体的面数和棱数即可．
【详解】解：观察图形可知：剩下几何体有7个面．
故答案为：7．
15. 已知，请写一个满足条件的的值________．
【答案】2（答案不唯一）
【解析】
【分析】本题考查绝对值，解一元一次不等式．根据绝对值的定义可求出的取值范围，再确定的值即可．
【详解】解：，
，
，
满足条件的的值可以为2（答案不唯一），
故答案为：2（答案不唯一）．
16. 如图，在一个边长为厘米的正方形铁板的四角，各剪去一个半径为厘米的圆，用式子表示阴影部分的面积为________平方厘米．
【答案】
【解析】
【分析】此题考查了列代数式．求出一个圆的面积，继而可得出空白部分的面积，然后根据阴影部分的面积正方形的面积空白部分的面积即可得出答案．
【详解】解：由题意得，圆的面积，
空白部分的面积，
阴影部分的面积正方形的面积空白部分的面积．
故答案为：．
三、解答题（17-22题每题6分，23、24每题8分，25、26每题10分，共72分）
17. 画数轴，在数轴上表示下列各数：，2，，，，4，并用“<”将它们连接起来．
【答案】数轴见解析，．
【解析】
【分析】此题主要考查了有理数的大小，以及数轴．首先在数轴上表示各数，然后再根据在数轴上右边的点表示的数大于左边的点表示的数用“<”号把它们连接起来．
【详解】解：如图所示：
故．
18. 计算：
（1）
（2）
【答案】（1）
（2）
【解析】
【分析】本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
（1）先算乘方，再算乘法，后算加减，即可解答；
（2）先算乘方，再算乘法，后算加减，有括号先算括号里，即可解答．
【小问1详解】
解：
；
【小问2详解】
解：
．
19. 先化简，在求值：，其中．
【答案】，
【解析】
【分析】本题主要考查了整式加减的化简求值，先根据整式加减混合运算法则进行计算，然后再代入求值即可．
【详解】解：
，
当时，原式．
20. 如图是由几个大小完全相同的正方体搭成的几何体，请在下面方格中画出这个几何体从正面、左面、上面看到的图形．
【答案】见解析
【解析】
【分析】根据三视图的定义以及画法画出相应的图形即可．
【详解】解：如图所示：
【点睛】本题考查的是由小正方体堆砌起来的组合体的三视图，理解视图的定义，掌握简单组合体的三视图的形状是正确解答的前提．
21. 如图是3个几何体的平面展开图．

（1）请写出对应几何体的名称：① ；② ；③
（2）图③中，侧面展开图的宽（较短边）为，圆的半径为，求图③所对应几何体的表面积．（结果保留）
【答案】（1）圆锥；三棱柱；圆柱
（2）
【解析】
【分析】（1）根据几何体的展开图，可得答案；
（2）根据圆柱表面积公式，可得答案．
【小问1详解】
解：对应几何体的名称：①圆锥；②三棱柱；③圆柱．
故答案为：圆锥；三棱柱；圆柱．
【小问2详解】
∵侧面展开图的宽（较短边）为，圆的半径为，
∴圆柱的表面积为：
．
∴图③所对应几何体的表面积．
【点睛】本题考查几何体的展开图和圆柱的表面积．熟练掌握几何体的展开图及圆柱表面积的计算公式是解题的关键．
22. 已知关于、的多项式，，．
（1）求；老师展示了一位同学的作业如下：
解：第一步
第二步
第三步
回答问题：这位同学第 步开始出现错误，错误原因是 ．
（2）若的结果与字母的取值无关，求的值．
【答案】（1）二；去括号时，第二项没有变号
（2）．
【解析】
【分析】本题考查整式的加减，熟练掌握去括号法则和合并同类项的方法是解答本题的关键．
（1）根据题目中的解答过程可知：这位同学第二步开始出现错误，错误原因是去括号时，第二项没有变号；
（2）先计算出，然后根据结果与字母的取值无关，即可求得的值．
【小问1详解】
解：由题目中的解答过程可知：这位同学第二步开始出现错误，错误原因是去括号时，第二项没有变号，
故答案为：二，去括号时，第二项没有变号；
【小问2详解】
解：
，
的结果与字母的取值无关，
，
解得．
23. 出租车司机刘师傅某日上午从地出发，在东西方向的公路上行驶营运，下表是每次行驶的里程（单位：千米）．（规定向东走为正，向西走为负；×表示空载，○表示载有乘客，且乘客都不相同）
（1）刘师傅走完第8次里程后，他在地的什么方向？离地有多少千米？
（2）已知出租车平均每行驶1千米耗电2度，刘师傅开始行驶前汽车电瓶储电150度，若少于5度电，则需要到附近的充电站充电，请通过计算说明刘师傅这天上午中途是否需要充电？
（3）已知载客时3千米以内收费9元，超过3千米后每千米收费1.6元，问刘师傅这天上午走完8次里程后营业额最多的一次是第几次，是多少元？
【答案】（1）刘师傅走完第8次里程后，他在地西边，离地有11千米；
（2）需要到附近的充电站充电；
（3）刘师傅这天上午走完8次里程后营业额最多的一次是第8次，是36.2元．
【解析】
【分析】本题考查了数轴，正负数，有理数的加减法，理解题意，正确列式是解题的关键．
（1）将各数相加所得的结果即是距出发点的距离，若得数为正，则在地的东边；若得数为负，则在地的西边；
（2）根据耗电量每千米的耗电量总路程，列式计算即可；
（3）观察表格，可知第8次里程最大，即营业额最多，然后按照计费标准计算即可．
【小问1详解】
解：
（千米），
答：刘师傅走完第8次里程后，他在地的西边，离地有11千米；
【小问2详解】
解：（度，
（度，
，
需要到附近的充电站充电；
【小问3详解】
解：由表格可知，第8次里程最大，即营业额最多，
（元，
答：刘师傅这天上午走完8次里程后营业额最多的一次是第8次，是36.2元．
24. 观察下列各式：
；；；；…．
（1）用你发现的规律填写下列式子的结果：；
（2）用你发现的规律计算：．
【答案】（1）见解析 （2）．
【解析】
【分析】本题考查了有理数乘法的规律探究，关键找到规律写出分数相乘的形式．
（1）根据等式规律写出分数相乘的形式计算结果．
（2）按规律写出分数相乘形式，再根据分数乘法进行约分求解．
【小问1详解】
解：；
【小问2详解】
解：
．
25. 概念学习
规定：求若干个相同的有理数(均不等于0)的除法运算叫做除方，如，等．类比有理数的乘方，我们把记作，读作“2的圈3次方”，记作，读作“的圈4次方”，一般地，把记作，读作“a的圈n次方”．

初步探究
（1）直接写出计算结果：______，______；
（2）关于除方，下列说法错误的是______，
A．任何非零数的圈2次方都等于1；
B．对于任何正整数n，；
C．
D．负数圈奇数次方结果是负数，负数的圈偶数次方结果是正数．
深入思考
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？
（1）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．______；______；=______．
（2）想一想：将一个非零有理数a的圈n次方写成幂的形式等于______；
（3）算一算：．
【答案】初步探究：（1），；（2）C；
深入思考：（1）； ；；（2）；（3）．
【解析】
【分析】初步探究：（1）根据所规定的a的圈n次方的定义，计算结果即可得到答案；
（2）根据所规定的a的圈n次方的定义，列式逐项计算验证是否正确即可．
深入思考：（1）根据有理数乘方运算的法则，原来的底数作底数，即可得解；
（2）根据所得式子得出总结规律即可得解．
（3）利用上面的结论，将除方运算转化为乘方运算，再用有理数混合运算法则计算即可．
【详解】解：初步探究：（1），
，
故答案为：，；
（2）A、任何非零数的圈2次方就是两个相同数相除，所以都等于1；所以选项A正确，不符合题意；
B、因为多少个1相除都是1，所以对于任何正整数n，都等于1；所以选项B正确，不符合题意；
C、，，则；所以选项C错误，符合题意；
D、负数的圈奇数次方，相当于奇数个负数相除，则结果是负数，负数的圈偶数次方，相当于偶数个负数相除，则结果是正数．所以选项D正确，不符合题意；
故选：C；
深入思考
（1）；
；
；
故答案为： ； ；；
（2）由（1）总结规律得：；
故答案为：；
（3）解：原式，
，
．
【点睛】此题考查了有理数的乘方运算，四则混合运算，正确掌握有理数运算的法则及正确理解题意列式计算是解题的关键．
26. 如图，点，都在数轴上，点为原点，设点，表示的数分别是、，且与满足．
（1）求与的值；
（2）若点到点的距离是到点距离的3倍，求点对应的数；
（3）若动点从点出发以3个单位长度/秒的速度向右运动，同时动点从点出发，以1个单位长度/秒的速度向左运动，设运动时间为秒，请用含的代数式表示、两点所对应的有理数．
【答案】（1），；
（2）对应的数为或．
（3）对应的数为，对应的数为．
【解析】
【分析】本题考查了一元一次方程的应用，非负数的性质及数轴上两点间的距离．
（1）根据绝对值和平方的非负性和为0求出a、b即可；
（2）设对应的数为，则，，利用点到点的距离是到点距离的3倍，再建立方程求解即可；
（3）根据数轴上表示有理数的方法：向右运动用加法，向左运动用减法表示P、Q对应的数即可．
【小问1详解】
解：∵，
∴，，
解得：，；
【小问2详解】
设对应的数为，则，，
∵点到点的距离是到点距离的3倍，
∴，
∴或，
解得：，，
∴对应的数为或．
【小问3详解】
∵动点从点出发以3个单位长度/秒的速度向右运动，同时动点从点出发，以1个单位长度/秒的速度向左运动，设运动时间为秒，
∴对应的数为，对应的数为．次数
1
2
3
4
5
6
7
8
里程
载客
×
○
○
×
○
○
×
○