





还剩15页未读,
继续阅读
第5章 平面直角坐标系 小结与思考 苏科版数学八年级上册课件
展开
这是一份第5章 平面直角坐标系 小结与思考 苏科版数学八年级上册课件,共23页。
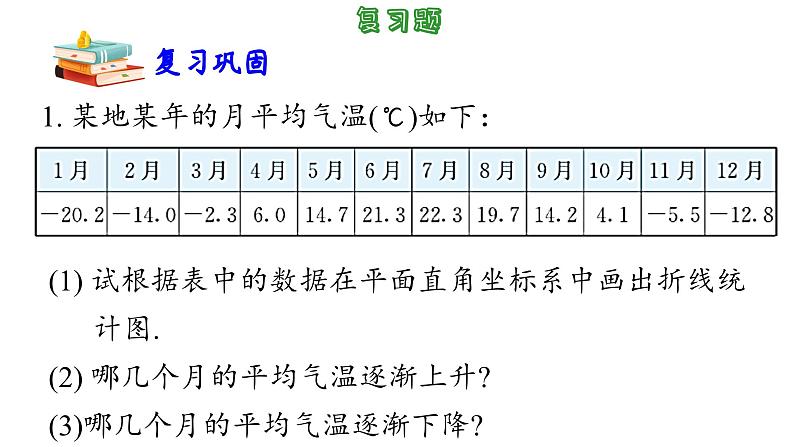
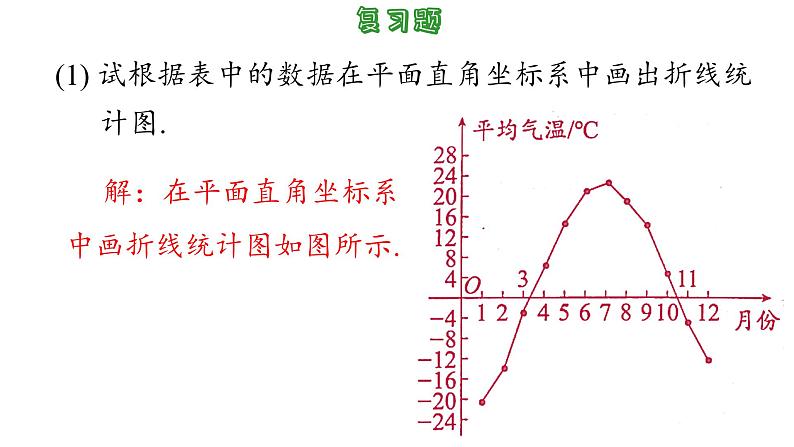
第5章 平面直角坐标系小结与思考 1. 平面直角坐标系的两条坐标轴互相垂直且有公共原点,两条坐标轴的单位长度通常相等。根据实际问题的需要,两条坐标轴的单位长度也可以不相等. 2. 在平面直角坐标系中,一对有序实数可以确定一个点的位置,一个点的位置也可以用一对有序实数来表示,这样就建立了数量变化与位置变化之间的联系. 3. 平面直角坐标系把坐标平面分为 4 个象限:第一象限、第二象限、第三象限、第四象限. 坐标轴不属于任何象限. 第一、二、三、四象限内点的坐标符号分别是(+,+)、(-,+)、(-, -) 、(+ , -). x 轴上点的横坐标为任意实数,纵坐标为 0; y 轴上点的横坐标为 0,纵坐标为任意实数. 4. 坐标平面内任意一点 P(a,b)关于 a 轴、y 轴、原点对称的点分别是点: P1(a, -b)、P2(-a,b)、P3(-a, -b). 5. 在探究有关实际问题时,常常通过建立恰当的平面直角坐标系,就可以用较为简明的坐标描述物体的位置、刻画一个图形,从而便于我们研究和解决问题.6. 举例说明平面直角坐标系在日常生活中的应用.复习题1. 某地某年的月平均气温(℃)如下:(1) 试根据表中的数据在平面直角坐标系中画出折线统 计图.(2) 哪几个月的平均气温逐渐上升?(3)哪几个月的平均气温逐渐下降?(1) 试根据表中的数据在平面直角坐标系中画出折线统 计图. 解:在平面直角坐标系中画折线统计图如图所示.(2) 哪几个月的平均气温逐渐上升?(3)哪几个月的平均气温逐渐下降?1月~7月的平均气温逐渐上升.7月~12月的平均气温逐渐下降.2. 根据下列各组点的坐标,在平面直角坐标系中分别 画出下列各组点,以这些点为顶点的图形分别是什 么图形? (1) A(2,1),B(4,1),C(4,5); (2) A(3,4),B(-3,4),C(0,-2); (3) A(1,0),B(0,1),C(-1,0),D(0,-1); (4) A(-2,3),B(3,4),C(3,-4),D(-2,-5).解:分别画图如图所示. (1)图1是直角三角形. (2)图2是等腰三角形. (3)图3是正方形. (4) 图 4 是平行四边形. 4. 填表:5. 如图,正方形 ABCD 的边长是4,写出它 的 4 个顶点及对角线 交点 E 的坐标.解:A (-1,-1), B (3,-1),C(3,3), D (-1,3),E(1,1).6. 填空: (1) 已知点 A(a,-b)、B(-a, -b)、C(-a,b),且 a≠0,b≠0. 其中,关于x轴对称的两点是_______和________; 关于 y 轴对称的两点是________和_________. (2) 已知点P(1-m,2-n). 如果 m>1、n<2,那么点P在第______象限; 如果 m=1,那么点P在________.点B点C点A点B二y轴上7. 填表:8. 小明在平面直角坐标系中 画了一幅图案(如图),他 怎样描述这幅图案,可以 使别人根据他的描述能画 出同样的图案?略9. 已知点A(0,0)、B(3,0),点 C 在 y 轴上,且△ABC 的面积是5. 求点 C 的坐标. 10. 平行四边形的两个顶点的坐标分别为(-3,0)、(1,0), 第 3个顶点在 y 轴上,且与 x 轴的距离为 3 个单位长 度,求第 4 个顶点的坐标, 解:第4 个顶点的坐标有 6 种可能,分别为(4,3),(-4,3),(-2,-3),如图1所示; (4,-3),(-4,-3),(-2,3),如图2所示.11. 在平面直角坐标系中,以点 A(-1,2)为一个顶点画 长方形,使它的两边分别与坐标轴平行,且两边长 分别为 3、4. 写出所画长方形的其余三个顶点的坐标.解:第一种情况如图1所示. 如果和 x轴平行的边的长是4,和y轴平行的边的长是 3,那么其余三个顶点的坐标分别为 ①B(3,2),C(3,-1), D(-1,-1); ②B′(3,2),C′(3,5), D′(-1,5); ③B″(-5,2),C″(-5,5),D″(-1,5); ④B″′(-5,2),C″′(-5,-1),D″′(-1,-1).第二种情况如图2所示. 如果和 x 轴平行的边的长是 3,和y 轴平行的边的长是 4.那么其余三个顶点的坐标分别为 ① B(2,2),C(2,-2),D(-1,-2); ② B′(2,2),C′(2,6),D′(-1,6); ③ B″(-4,2),C″(-4,6),D″(-1,6); ④ B′′′ (-4,2),C′′′ (-4,-2),D′′′ (-1,-2).
第5章 平面直角坐标系小结与思考 1. 平面直角坐标系的两条坐标轴互相垂直且有公共原点,两条坐标轴的单位长度通常相等。根据实际问题的需要,两条坐标轴的单位长度也可以不相等. 2. 在平面直角坐标系中,一对有序实数可以确定一个点的位置,一个点的位置也可以用一对有序实数来表示,这样就建立了数量变化与位置变化之间的联系. 3. 平面直角坐标系把坐标平面分为 4 个象限:第一象限、第二象限、第三象限、第四象限. 坐标轴不属于任何象限. 第一、二、三、四象限内点的坐标符号分别是(+,+)、(-,+)、(-, -) 、(+ , -). x 轴上点的横坐标为任意实数,纵坐标为 0; y 轴上点的横坐标为 0,纵坐标为任意实数. 4. 坐标平面内任意一点 P(a,b)关于 a 轴、y 轴、原点对称的点分别是点: P1(a, -b)、P2(-a,b)、P3(-a, -b). 5. 在探究有关实际问题时,常常通过建立恰当的平面直角坐标系,就可以用较为简明的坐标描述物体的位置、刻画一个图形,从而便于我们研究和解决问题.6. 举例说明平面直角坐标系在日常生活中的应用.复习题1. 某地某年的月平均气温(℃)如下:(1) 试根据表中的数据在平面直角坐标系中画出折线统 计图.(2) 哪几个月的平均气温逐渐上升?(3)哪几个月的平均气温逐渐下降?(1) 试根据表中的数据在平面直角坐标系中画出折线统 计图. 解:在平面直角坐标系中画折线统计图如图所示.(2) 哪几个月的平均气温逐渐上升?(3)哪几个月的平均气温逐渐下降?1月~7月的平均气温逐渐上升.7月~12月的平均气温逐渐下降.2. 根据下列各组点的坐标,在平面直角坐标系中分别 画出下列各组点,以这些点为顶点的图形分别是什 么图形? (1) A(2,1),B(4,1),C(4,5); (2) A(3,4),B(-3,4),C(0,-2); (3) A(1,0),B(0,1),C(-1,0),D(0,-1); (4) A(-2,3),B(3,4),C(3,-4),D(-2,-5).解:分别画图如图所示. (1)图1是直角三角形. (2)图2是等腰三角形. (3)图3是正方形. (4) 图 4 是平行四边形. 4. 填表:5. 如图,正方形 ABCD 的边长是4,写出它 的 4 个顶点及对角线 交点 E 的坐标.解:A (-1,-1), B (3,-1),C(3,3), D (-1,3),E(1,1).6. 填空: (1) 已知点 A(a,-b)、B(-a, -b)、C(-a,b),且 a≠0,b≠0. 其中,关于x轴对称的两点是_______和________; 关于 y 轴对称的两点是________和_________. (2) 已知点P(1-m,2-n). 如果 m>1、n<2,那么点P在第______象限; 如果 m=1,那么点P在________.点B点C点A点B二y轴上7. 填表:8. 小明在平面直角坐标系中 画了一幅图案(如图),他 怎样描述这幅图案,可以 使别人根据他的描述能画 出同样的图案?略9. 已知点A(0,0)、B(3,0),点 C 在 y 轴上,且△ABC 的面积是5. 求点 C 的坐标. 10. 平行四边形的两个顶点的坐标分别为(-3,0)、(1,0), 第 3个顶点在 y 轴上,且与 x 轴的距离为 3 个单位长 度,求第 4 个顶点的坐标, 解:第4 个顶点的坐标有 6 种可能,分别为(4,3),(-4,3),(-2,-3),如图1所示; (4,-3),(-4,-3),(-2,3),如图2所示.11. 在平面直角坐标系中,以点 A(-1,2)为一个顶点画 长方形,使它的两边分别与坐标轴平行,且两边长 分别为 3、4. 写出所画长方形的其余三个顶点的坐标.解:第一种情况如图1所示. 如果和 x轴平行的边的长是4,和y轴平行的边的长是 3,那么其余三个顶点的坐标分别为 ①B(3,2),C(3,-1), D(-1,-1); ②B′(3,2),C′(3,5), D′(-1,5); ③B″(-5,2),C″(-5,5),D″(-1,5); ④B″′(-5,2),C″′(-5,-1),D″′(-1,-1).第二种情况如图2所示. 如果和 x 轴平行的边的长是 3,和y 轴平行的边的长是 4.那么其余三个顶点的坐标分别为 ① B(2,2),C(2,-2),D(-1,-2); ② B′(2,2),C′(2,6),D′(-1,6); ③ B″(-4,2),C″(-4,6),D″(-1,6); ④ B′′′ (-4,2),C′′′ (-4,-2),D′′′ (-1,-2).
相关资料
更多









