第3章 勾股定理小结与思考 苏科版八年级数学上册课件

这是一份第3章 勾股定理小结与思考 苏科版八年级数学上册课件，共18页。

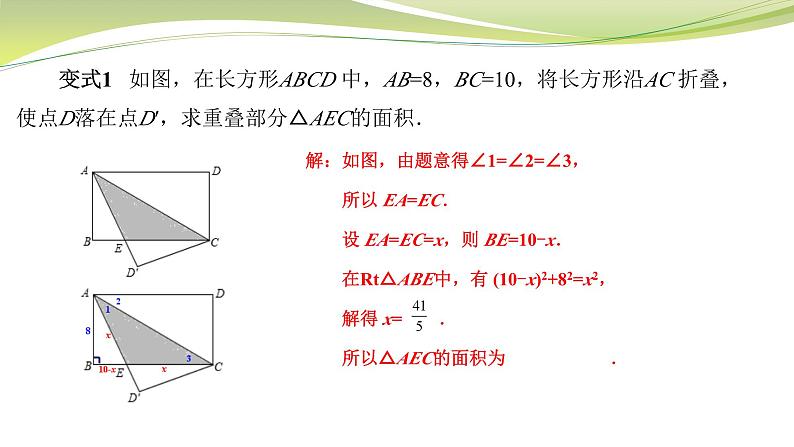
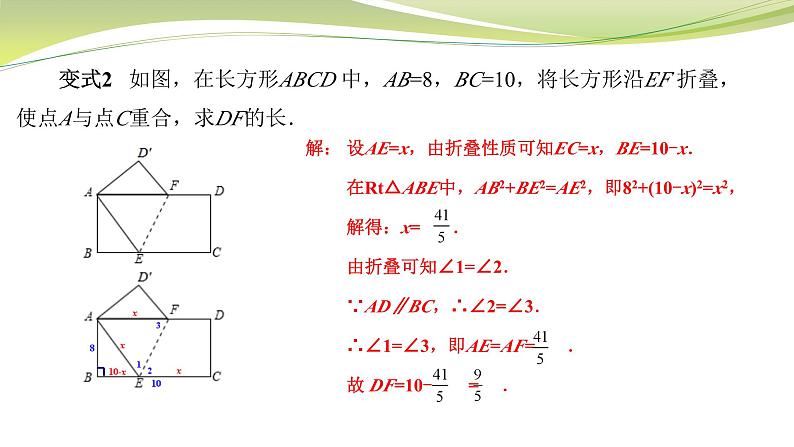
勾股定理及其应用（2）【典型例题】 例1 如图，已知：在Rt△ABC中，两直角边AC、BC的长分别为6和8，现将直角边AC沿AD折叠，使它落在斜边AB上，且与AE重合，求CD的长． 解：如图，Rt△ABC中，AC=6，BC=8，由勾股定理得AB=10． 由折叠性质可得AE=AC=6，DE=DC，∠AED=∠C=90°， 则BE=4，∠BED=90°． 设DC= DE=x，则BD=8-x． 在Rt△BDE中，由勾股定理得 x2+42=(8-x)2， 解得x=3．即CD=3． 变式1 已知：如图，在Rt△ABC中，两直角边AC、BC的长分别为6和8，现将△ABC折叠，使点B与A重合，折痕为DE，求CD的长．解： 如图，设CD=x， 则由折叠性质可得AD=BD=8-x． 在Rt△ACD中，由勾股定理得x2+62=(8-x)2， 解得x= ． 即CD= ． 变式2 已知：如图，在Rt△ABC中，两直角边AC、BC的长分别为6和8，现将△ABC折叠，使A点与BC的中点F重合，折痕为DE，求CD的长．解： 设CD=x， 由折叠的性质可得DF=AD=6-x． ∵F是BC的中点，∴CF=4． 在Rt△CDF中，x2+42=(6-x) 2， 解得 x= ． 即CD= ． 【题后小结】 在直角三角形中： 1、如果“已知a，b或a，c或b，c，求c或b或a”问题，就可以直接“运用勾股定理计算”求出第三边； 2、如果“已知a，c±b或b，c±a，求b和c”问题，我们可以通过“设未知数，运用勾股定理列方程”来解决． 【典型例题】 例2 如图，在长方形ABCD 中，AB=8，BC=10，将长方形沿AE折叠，使点D落在BC边上的点F处，求CE的长． 解：∵四边形ABCD为长方形， ∴AD=BC=10，CD=AB=8，∠B=∠C=90°． 由折叠性质得：AF=AD=10，EF=DE． Rt△ABF中，由勾股定理得：BF2=102-82=36， ∴BF=6，CF=10-6=4． 设CE=x，则EF=ED=8-x． 在Rt△EFC中，EF2=FC2+EC2，即(8-x)2=42+x2． 解得：x=3．即CE=3 ． 变式1 如图，在长方形ABCD 中，AB=8，BC=10，将长方形沿AC 折叠，使点D落在点D′，求重叠部分△AEC的面积．解：如图，由题意得∠1=∠2=∠3， 所以 EA=EC． 设 EA=EC=x，则 BE=10-x． 在Rt△ABE中，有 (10-x)2+82=x2， 解得 x= ． 所以△AEC的面积为 ． 变式2 如图，在长方形ABCD 中，AB=8，BC=10，将长方形沿EF 折叠，使点A与点C重合，求DF的长．解： 设AE=x，由折叠性质可知EC=x，BE=10-x． 在Rt△ABE中，AB2+BE2=AE2，即82+(10-x)2=x2， 解得：x= ． 由折叠可知∠1=∠2． ∵AD∥BC，∴∠2=∠3． ∴∠1=∠3，即AE=AF= ． 故 DF=10- = ． 变式3 如图，在长方形ABCD 中，AB=8，BC=10，将长方形沿MN折叠，使点B落在CD边上的中点E处，求AM的长．解一：如图，连接ME．由折叠性质可知MF=MA，EF=AB=8． ∵点E是CD的中点，∴DE=4． ∴在Rt△EFM中，有MF2+EF2=ME2， 在Rt△DEM中，有MD2+DE2=ME2， ∴MF2+EF2=MD2+DE2． 设AM=x，则DM=10-x， ∴x2+82=(10-x)2+42． 解得 x= ，即AM= ． 变式3 如图，在长方形ABCD 中，AB=8，BC=10，将长方形沿MN折叠，使点B落在CD边上的中点E处，求AM的长．解二：如图，连接MB、ME．由折叠性质可知MB=ME． ∵点E是CD的中点，∴DE=4． ∴在Rt△ABM中，有AM2+AB2=BM2， 在Rt△DEM中，有DM2+DE2=EM2， ∴AM2+AB2=DM2+DE2． 设AM=x，则DM=10-x， ∴x2+82=(10-x)2+42． 解得x= ， 即AM= ． 【题后小结】 解决这类折叠问题，首先抓住折叠变换是全等变换，折叠前后的对应边（角）大小不变；然后结合其他题设进行推理和转化；最后把所有条件集中到一个直角三角形中，用勾股定理列方程解得． 【典型例题】 例3 如图，在锐角△ABC中，已知：AB=13，BC=14，AC=15．求△ABC的面积．解：过点A作BC的高，交BC于点D，如图，设BD=x． 则在Rt△ABD中，根据勾股定理有：AD2=132-x2； 在Rt△ACD中，根据勾股定理有：AD2=152-(14-x)2． ∴132-x2=152-(14-x)2，解得x=5． ∴AD2=132-52=144，∴AD=12． 故S△ABC= BC×AD= ×14×12=84．变式1 如图，在钝角△ABC中，已知：BC=9，AB=10，AC=17．求△ABC的面积．解一：过点B作AC的高，交CA于点D，如图2，设AD=x． 则在Rt△ABD中，根据勾股定理有：BD2=102-x2； 在Rt△BCD中，根据勾股定理有：BD2=92-(17-x)2． ∴102-x2=92-(17-x)2，解得x= ．∴BD= ． 故S△ABC= AC×BD= ×17× =36．变式1 如图，在钝角△ABC中，已知：BC=9，AB=10，AC=17．求△ABC的面积．解二：过点A作BC的高，交CB的延长线于点D，如图1， 设BD=x，则CD=x+9． 在Rt△ABD中，根据勾股定理有：AD2=102-x2； 在Rt△ACD中，根据勾股定理有：AD2=172-(x+9)2． ∴102-x2=172-(x+9)2，解得x=6．∴AD=8． 故S△ABC= BC×AD= ×9×8=36． 变式2 如图，在△ABC中，若AC=4，AB=5，BC=6，AD为高，AE为中线．求DE的长．解：设DE=x，则BD=3+x，CD=3-x． 在Rt△ABD中，根据勾股定理有：AD2=52-(3+x)2； 在Rt△ACD中，根据勾股定理有：AD2=42-(3-x)2． ∴52-(3+x)2=42-(3-x)2． 解得x= ．即DE = ． 【题后小结】 如果题目中没有直角三角形，我们可以作高构造直角三角形，“化斜为直”将一般三角形问题转化为直角三角形的问题求解；在用勾股定理列方程时，需要注意选择合适的线段设为未知数，必要时可使用多次勾股定理． 【课堂小结】 1．勾股定理和勾股定理的逆定理： 2．能运用勾股定理通过“列方程”解决“已知a，c±b或b，c±a，求b和c”问题． 谢谢！