北师大版八年级下册2 平行四边形的判定示范课ppt课件

这是一份北师大版八年级下册2 平行四边形的判定示范课ppt课件，共38页。PPT课件主要包含了学习目标，新课导入，回顾与思考，概念剖析，定义法，证一证，证明连接AC，平行四边形的定义，∴BCDA，又∵ABCD等内容，欢迎下载使用。

1.理解平行四边形的两个判别条件，并会证明2.会运用平行四边形的定义及两个判别条件判别一个四边形是否为平行四边形
1.平行四边形的性质有哪些？
平行四边形对边平行；平行四边形对边相等；平行四边形对角相等；平行四边形对角线互相平分；
一、平行四边形的判定方法
想一想：具备什么条件的四边形是平行四边形？
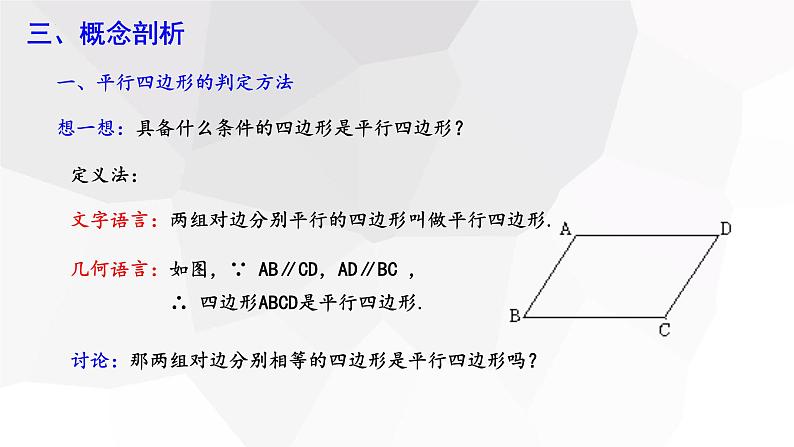
文字语言：两组对边分别平行的四边形叫做平行四边形.
几何语言：如图，∵ AB∥CD，AD∥BC ， ∴ 四边形ABCD是平行四边形.
讨论：那两组对边分别相等的四边形是平行四边形吗？
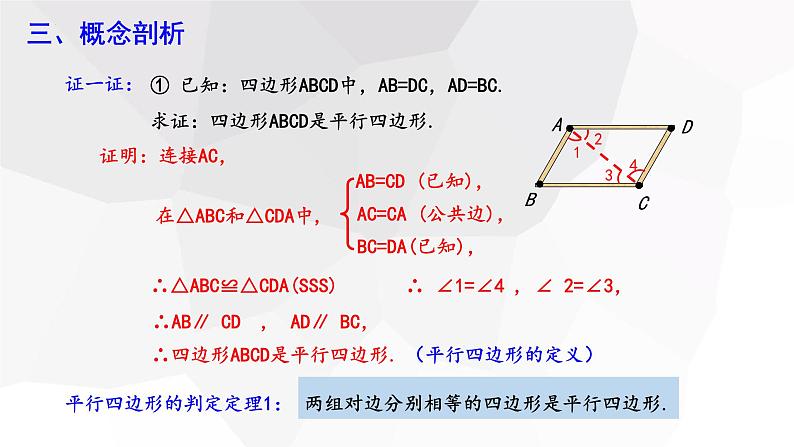
① 已知：四边形ABCD中，AB=DC，AD=BC.求证：四边形ABCD是平行四边形.
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3，
∴AB∥ CD , AD∥ BC，
∴四边形ABCD是平行四边形.
平行四边形的判定定理1：
两组对边分别相等的四边形是平行四边形.
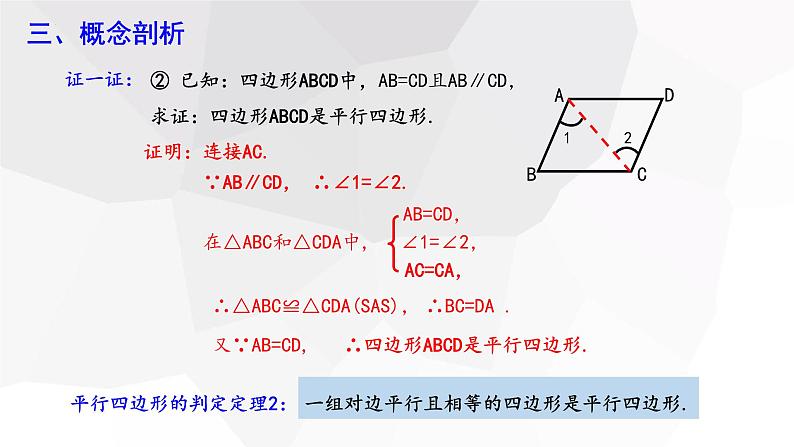
② 已知：四边形ABCD中，AB=CD且AB∥CD，求证：四边形ABCD是平行四边形.
∵AB∥CD， ∴∠1=∠2.
∴△ABC≌△CDA(SAS)，
平行四边形的判定定理2：
一组对边平行且相等的四边形是平行四边形.
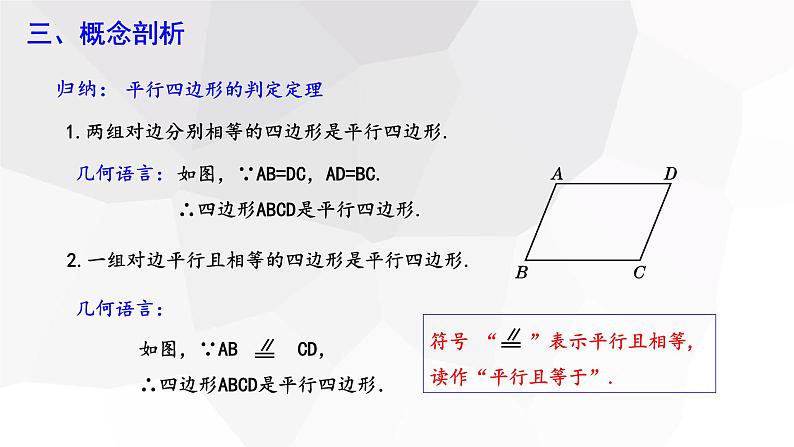
1.两组对边分别相等的四边形是平行四边形.
2.一组对边平行且相等的四边形是平行四边形.
如图，∵AB=DC，AD=BC.∴四边形ABCD是平行四边形.
例1.已知：如图，在平行四边形ABCD中，E， F分别为AD和CB的中点.求证：四边形BFDE是平行四边形.
分析：利用平行四边形的性质(对边平行且相等)再结合线段中点的性质得出ED与FB的关系，即可对四边形BFDE进行判定.
∵四边形ABCD是平行四边形，∴AD＝CB(平行四边形的对边相等),AD∥CB(平行四边形的定义）.∵E，F分别是AD和CB的中点，∴ED＝FB，ED∥FB.∴四边形DFDE是平行四边形.(一组对边平行且相等的四边形是平行四边形)
1.四边形AEFD和EBCF都是平行四边形，求证：四边形ABCD 是平行四边形.
证明：∵四边形AEFD和EBCF都是平行四边形，
∴AD∥ EF，AD=EF，
EF∥ BC，EF=BC.
∴AD∥ BC，AD=BC.
∴四边形ABCD是平行四边形．
例2.如图，已知E，F，G，H分别是▱ABCD的边AB，BC，CD，DA上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形．
证明：在平行四边形ABCD中，
∠A=∠C，AD=BC,
∴△AEH≌△CGF（SAS），
同理得△BEF≌△DGH（SAS），
∴四边形EFGH是平行四边形．（两组对边分别相等的四边形是平行四边形）
2.如图，在四边形ABCD中，(1)如果∠A：∠B：∠ C：∠D=a：b：a：b(a,b为正数),那么四边形ABCD是 四边形.(2)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
注意：两组对角分别相等的四边形是平行四边形.
3.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥AD,CF⊥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
∴Rt△AED≌Rt△CFB(AAS).
两组对边分别平行的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
6.2 平行四边形的判定
1.经历平行四边形判定方法3的探究过程，学会运用“对角线互相平分的四边形是平行四边形”进行判定2.能综合运用平行四边形的四种判定方法进行证明
如图，一个木匠，将两根木条AC，BD的中点重叠，并用钉子固定就得到了一个平行四边形ABCD，木匠的做法有什么依据吗？
依据：平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形吗？
例1.已知：四边形ABCD中，OA=OC，OB=OD. 求证：四边形ABCD是平行四边形.
证明：在△AOB和△COD中,
∴△AOB≌△COD(SAS)，
∴∠BAO=∠OCD ,
平行四边形的判定定理3：
对角线互相平分的四边形是平行四边形.
对角线互相平分的四边形是平行四边形．数学表达式：如图，∵OA=OC，OB=OD， ∴四边形ABCD是平行四边形．
方法总结：在判定平行四边形时，要根据题意灵活选择判定方法，有时要注意结合平行四边形的性质和判定三角形全等的方法，先得出边、角关系，再进行判定.
1.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　） A．OA=OC，OB=OD B．AB=CD，AO=CO C．AB=CD，AD=BC D．∠BAD=∠BCD，AB∥CD
2.如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD∥BC．求证：四边形ABCD是平行四边形．
证明：∵O是AC的中点，
∴∠ADO=∠CBO，
在△AOD和△COB中，
∴△AOD≌△COB（AAS），
例2.如图，□ABCD的对角线AC,BD相交于点O，E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.（对角线互相平分的四边形的平行四边形）
分析：首先利用平行四边形的性质，得出对角线互相平分，进而得出EO=FO，BO=DO，即可对四边形BFDE进行判定.
3.如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为(　　 )
A．6 B．12 C．20 D．24
4.如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E，F分别是OA和OC的中点，四边形BFDE是平行四边形吗？请说明理由.
四边形BFDE是平行四边形，理由：∵四边形ABCD是平行四边形，∴OB＝OD，OA＝OC.又∵E，F分别是OA和OC的中点，∴OE＝OF.
∴四边形BFDE是平行四边形．
5.已知：如图，AC是平行四边形ABCD的对角线，BM⊥AC，DN⊥AC，垂足分别是M、N．求证：四边形BMDN是平行四边形
证明：∵BM⊥AC，DN⊥AC，∴∠DNA=∠BMC=90°，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴△ADN≌△CBM，∴四边形BMDN是平行四边形．
∴∠DAN=∠BCM，
1.两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法：
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.对角线互相平分的四边形是平行四边形.
1.理解平行线之间的距离的概念、并能运用这一概念解决相关问题2.能根据题意灵活运用平行四边形的性质和判定解决问题
数学来源于生活，高铁被外媒誉为我国新四大发明之一，在笔直的铁轨上，夹在铁轨之间的平行枕木是否一样长？你能说明理由吗?与同伴交流.
例1.已知：如图,直线 a∥b ，A、B是直线a上任意两点，AC⊥b，BD⊥b，垂足分别为C，D. 求证：AC=BD.
证明：∵AC⊥CD，BD⊥CD，∴∠1=∠2=90°.∵ AB∥CD.∴ 四边形ACDB是平行四边形(平行四边形的定义).∴ AC=BD (平行四边形的对边相等).
结论：夹在两条平行线间的任何平行线段都相等.
如果两条直线互相平行，则其中一条直线上任意两点到另一条直线的距离相等，这个距离称为平行线之间的距离.
数学表达式：如图，A，C是 l1 上任意两点，∵l1 ∥ l2，AB⊥ l2，CD ⊥ l2，∴AB = CD.
1.如图所示，l1∥l2，AB∥CD，CE⊥l1，FG⊥l2，E、G为垂足，则下列说法中错误的是（　　） A．CD＞CE B．A、B两点间的距离就是线段AB的长 C．CE=FG D．l1、l2间的距离就是线段CD的长
2.如图(1)，已知直线a∥b，点A，E，F在直线a上，点B，C，D在直线b上，BC=EF. △ABC与△DEF的面积相等吗？为什么？
解：△ABC和△DEF的面积相等．理由如下：如图(2)，作AH1⊥直线b，垂足为点H1，作DH2⊥直线a，垂足为点H2.
设△ABC和△DEF的面积分别为S1和S2，∴ S1= BC·AH1，S2= EF·DH2.∵直线a∥b，AH1⊥直线b，DH2⊥直线a，∴AH1=DH2.又∵BC=EF，即△ABC与△DEF的面积相等．
结论：等底等高的三角形的面积相等．
例2.如图，在平行四边形ABCD中,点M、N分别是AD、BC上的两点，点E、F在对角线BD上，且DM=BN，BE=DF. 求证：四边形MENF是平行四边形.
证明：∵四边形ABCD是平行四边形， ∴AD∥CB， ∵DM=BN ，DF=BE ∴△MDF≌△NBE ∴MF=EN，∠MFD=∠NEB ∴∠MFE=∠NEF， ∴四边形MENF是平行四边形.
3.如图，在▱ABCD中，E，F分别为BC，AD边上的点，要使BF=DE，需添加一个条件：_______________________．
BF∥DE(答案不唯一)
4.如图：平行四边形ABCD中，∠ABC=70°，∠ABC的平分线交AD于点E，过 D作BE的平行线交BC于点F，求∠CDF的度数.
解：∵BE是∠ABC的平分线，∠ABC=70°，∴∠ABE=∠CBE=35°，∠ADC=∠ABC=70°，在▱ABCD中，∵AD∥BC，∴∠EBF=∠AEB=35°，∵DF∥BE，∴∠ADF=∠AEB=35°，∴∠CDF=35°．