河南省南阳市南召县2023－2024学年九年级上学期期末巩固练习数学试卷

这是一份河南省南阳市南召县2023－2024学年九年级上学期期末巩固练习数学试卷，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题(每小题3分；共30分)
1-5 BADCD 6-10 ACBDC
二、填空题(每小题3分，共15分)
11．2; 12．8; 13．; 14．y1＜y2＜y3; 15．或
三、解答题(10+9+9+9+9+9+10+10=75分)
16．解：（1）原式分
分
分
（2）分.
分
分
17．解：如图，点E即为所求.
分(无作图痕迹不给分)
证明：由作图知，∠C=∠ADE，
又∠A=∠A
所以，△ADE∽△ACB 分
18．解：（1）∵关于x的方程x2+（2k－1）x+k2－1＝0有两个实数根x1和x2．
∴Δ＝（2k－1）2－4（k2－1）＝－4k+5≥0，分
∴分
（2）∵x1+x2＝1－2k，x1·x2=k2－1，
，
∴(x1+x2)2＝3x1x2+16，分
∴（1－2k）2＝3（k2－1）+16，
即k2－4k－12＝0，
解得：k＝6或k＝－2，分
∵，
∴k＝－2．分
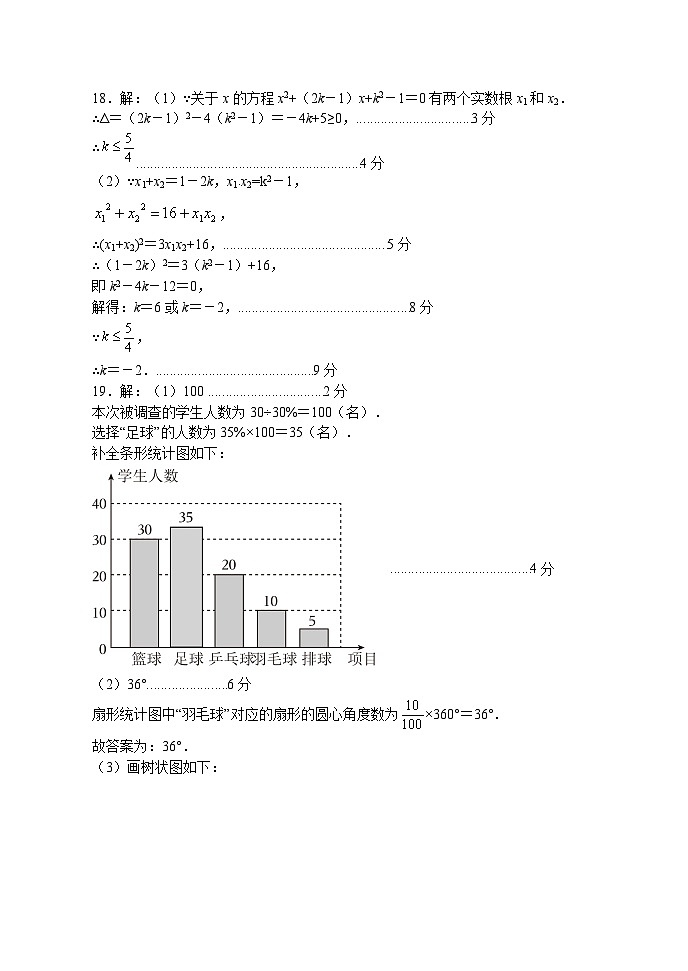
19．解：（1）100 分
本次被调查的学生人数为30÷30%＝100（名）．
选择“足球”的人数为35%×100＝35（名）．
补全条形统计图如下：
分
（2）36°分
扇形统计图中“羽毛球”对应的扇形的圆心角度数为×360°＝36°．
故答案为：36°．
（3）画树状图如下：
分
共有12种等可能的结果，其中甲和乙同学同时被选中的结果有2种，
∴甲和乙同学同时被选中的概率为． 分
20．解：连结BC交AF于D，由题意可知，四边形BEFD和四边形DFGC均为矩形，
在Rt△ABC中，设BD为x m，分
∵tan∠ABD＝，
∴AD＝BD•tan∠ABD≈2.14x ，分
∴CD＝（80－x）m，分
在Rt△ACD中，AD＝CD＝（80－x），
∴2.14x＝80－x，
∴x≈25.48，分
∴AD＝80－x＝54.52，
∴AF＝AD+DF＝54.52+1.5＝56.02≈56（m），分
答：铁塔的高度约为56 m． 分
21．解：（1）设，函数关系为：y＝kx+b，
，
解得：．
∴y＝－2x+200． 分
设日获得利润为w元，则
w＝（－2x+200）（x－30－4） 分
＝－2（x－67）2+2178， 分
∵a＝－2＜0，
∴当x＜67时，w的值随x值的增大而增大， 分
∵售价不低于50×0.8＝40，
∴40≤x≤50， 分
∴当x＝50时．=1600 分
答：这种蔬菜的售价为50元，利润为1600元．
22．解：（1）∵D（0，4），
∴OD＝4，
∵OA＝OD，点A在x的负半轴上，
∴A（－4，0）， 分
把A（－4，0），D（0，4）分别代入y1＝ax2－3x+c，得，
解得：，
∴该抛物线的解析式为y1＝－x2－3x+4， 分
把A（－4，0）代入y2＝－x+b，得4+b＝0，
解得：b＝－4； 分
（2）存在．
在y1＝－x2－3x+4中，令y1＝0，得－x2－3x+4＝0，
解得：x1＝－4，x2＝1，
∴B（1，0），
如图1，设直线y2＝－x－4与y轴交于点G，
则G（0，－4），
∴OG＝4，
∵A（－4，0），
∴OA＝4，
∴OA＝OG，
∴△AOG是等腰直角三角形，
∴∠BAC＝45°，
当∠APB＝90°时，如图1，过点P作PH⊥x轴于点H，
∵∠BAP＝45°，∠APB＝90°，
∴∠ABP＝45°＝∠BAP，
∴PA＝PB，即△ABP是等腰直角三角形，
∵PH⊥AB，
∴AH＝BH，即H是AB的中点，
∴H（－，0），
∴点P的横坐标为－，
当x＝－时，y2＝－（－）－4＝－，
∴P1（－，－）； 分
当∠ABP＝90°时，则∠APB＝∠BAP＝45°，
∴BP＝AB＝5，
∴P2（1，－5）；分
综上所述，在直线y2＝－x－4上存在点P使得△ABP是等腰直角三角形，点P的坐标为（－，－）或（1，－5）；
（3）－8＜n＜－4． 分
解析：∵y1＝－x2－3x+4＝－（x+）2+，
∴抛物线y1＝－x2－3x+4的顶点为（－，），沿x轴翻折后的解析式为
y＝（x+）2－，
把A（－4，0）代入y3＝－x+n，得4+n＝0，
解得：n＝－4，
联立抛物线y＝（x+）2－与直线y3得：
（x+）2－＝－x+n，
整理得：x2+4x－（n+4）＝0，
当Δ＝16+4（n+4）＝0时，n＝－8，
∴当直线y3＝－x+n与该新图象恰好有四个公共点时，－8＜n＜－4．
23．解：（1）ME＝MF． 分
（2）ME＝MF．分
解析：过点M作MH⊥AD于H，MG⊥AB于G，连接AM．
∵M是菱形ABCD的对称中心，
∴O是菱形ABCD对角线的交点，
∴AM平分∠BAD，
∴MH＝MG．
∵∠EMF＝∠ABC
，∴∠EMF+∠BAD＝180°．
又∠MHA＝∠MGF＝90°，
∴∠HMG+∠BAD＝180°．
∴∠EMF＝∠HMG．
∴∠EMH＝∠FMG．
∵∠MHE＝∠MGF，
∴△MHE≌△MGF，
∴ME＝MF．
（3）ME∶MF＝1∶2 5分
理由：过点M作MH⊥AD于H，MG⊥AB于G．
∵∠EMF＝∠B，∴∠A＝∠EMF＝90°．
又∵∠MHA＝∠MGA＝90°，
∴∠HMG＝90°．
∴∠EMF＝∠HMG，∴∠EMH＝∠FMG．
∵∠MHE＝∠MGF，
∴△MHE∽△MGF，
∴＝． 分
又∵M是矩形ABCD的对称中心，
∴M是矩形ABCD对角线的中点．
又∵MG⊥AB，
∴MG∥BC，
∴MG＝BC．
同理可得MH＝AB．.
又∵AB∶BC=1∶2 ∴MH∶MG=1∶分
∴ME∶MF＝1∶2． 分
（4）结论：ME∶MF＝m． 分
解析：由（3）可知：△MHE∽△MGF，
∴＝＝＝m．