

人教版16.2 二次根式的乘除教案
展开第二课时:二次根式的除法
最简二次根式
教学内容
二次根式的乘法
课时数
1
学科
数学
年级
八年级
班级
教学目标
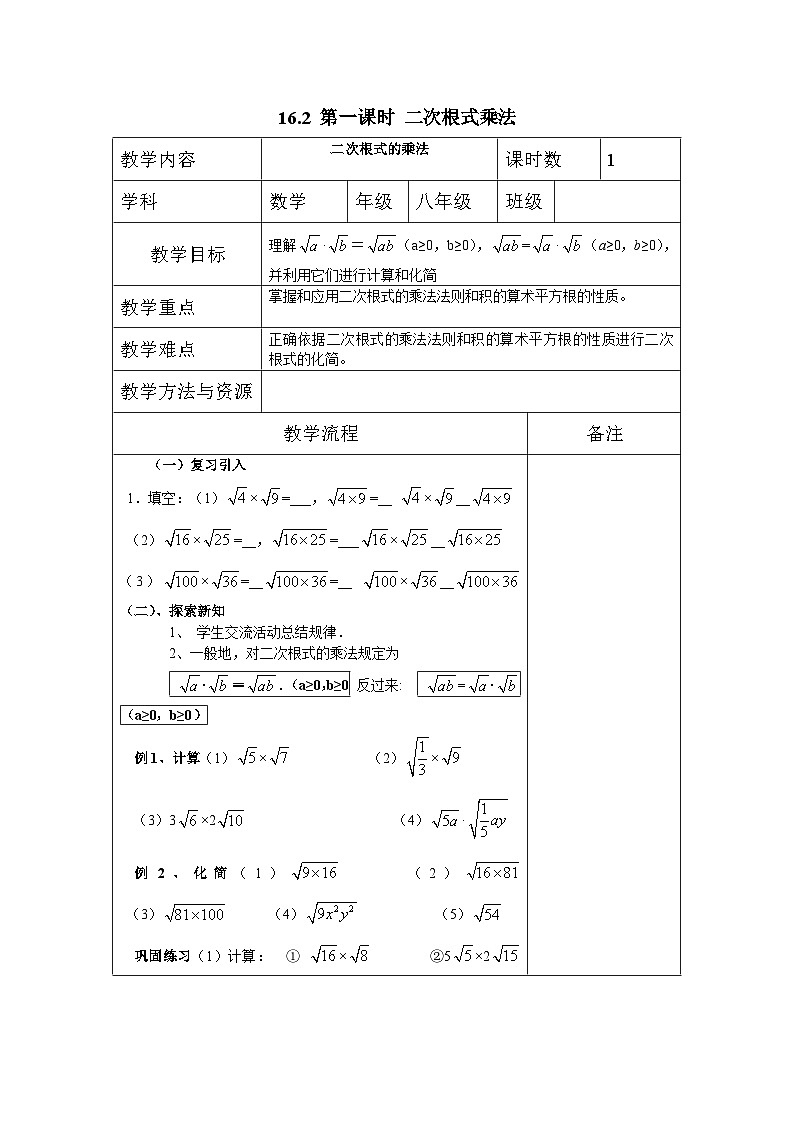
理解·=(a≥0,b≥0),=·(a≥0,b≥0),并利用它们进行计算和化简
教学重点
掌握和应用二次根式的乘法法则和积的算术平方根的性质。
教学难点
正确依据二次根式的乘法法则和积的算术平方根的性质进行二次根式的化简。
教学方法与资源
教学流程
备注
(一)复习引入
1.填空:(1)×=___,=__ ×__
(2)×=__,=___×__
(3)×=__=__ ×__(二)、探索新知
1、 学生交流活动总结规律.
2、一般地,对二次根式的乘法规定为
·=.(a≥0,b≥0 反过来: =·(a≥0,b≥0)
例1、计算(1)× (2)×
(3)3×2 (4)·
例2、化简(1) (2) (3) (4) (5)
巩固练习(1)计算: ① × ②5×2 ③·
(2)化简: ; ; ; ;
(三)、学生小组交流解疑,教师点拨、拓展
判断下列各式是否正确,不正确的请予以改正:
(1)
(2)×=4××=4×=4=8
(四)展示反馈
(五)达标测试:
A组
1、选择题
(1)等式成立的条件是( )
A.x≥1 B.x≥-1 C.-1≤x≤1 D.x≥1或x≤-1
(2)下列各等式成立的是( ).
A.4×2=8 B.5×4=20
C.4×3=7 D.5×4=20
(3)二次根式的计算结果是( )
A.2 B.-2 C.6 D.12
2、化简: (1); (2);
3、计算: (1); (2);
B组
1、选择题
(1)若,则=( )
A.4 B.2 C.-2 D.1
(2)下列各式的计算中,不正确的是( )
A.=(-2)×(-4)=8
B.
C.
D.2、计算:(1)6×(-2); (2);
3、不改变式子的值,把根号外的非负因式适当变形后移入根号内。
(1) -3 (2)
板书设计
教学反思
教学内容
二次根式的除法
课时数
1
学科
数学
年级
八年级
班级
教学目标
1、掌握二次根式的除法法则和商的算术平方根的性质。
2、能熟练进行二次根式的除法运算及化简。
教学重点
掌握和应用二次根式的除法法则和商的算术平方根的性质。
教学难点
正确依据二次根式的除法法则和商的算术平方根的性质进行二次根式的化简。
教学方法与资源
教学流程
备注
(一)复习回顾
1、写出二次根式的乘法法则和积的算术平方根的性质
2、计算: (1)3×(-4) (2)
3、填空:(1)=____,=____;规律: __
(2)=____,=____; ______;
(3)=____,=____; _______;
(4)=____,=___. _______.
一般地,对二次根式的除法规定:
=(a≥0,b>0)反过来,=(a≥0,b>0)
下面我们利用这个规定来计算和化简一些题目.
(二)、巩固练习
1、计算:(1) (2)
(3) (4)
2、化简:
(1) (2) (3) (4)
注:1、当二次根式前面有系数时,类比单项式除以单项式法则进行计算:即系数之商作为商的系数,被开方数之商为被开方数。
2、化简二次根式达到的要求:
(1)被开方数不含分母;
(2)分母中不含有二次根式。
(三)拓展延伸
阅读下列运算过程:
数学上将这种把分母的根号去掉的过程称作“分母有理化”。
利用上述方法化简:
(1) =_______ (2)=________(3) =_____ ___ (4) =___ ___
(四)达标测试:
A组
1、选择题
(1)计算的结果是( ).
A. B. C. D.
(2)化简的结果是( )
A.- B.- C.- D.-
2、计算:
(1) (2) (3) (4)
B组
用两种方法计算:
(1) (2)
板书设计
教学反思
教学内容
最简二次根式
课时数
1
学科
数学
年级
八年级
班级
教学目标
1、理解最简二次根式的概念。
2、把二次根式化成最简二次根式.
3、熟练进行二次根式的乘除混合运算。
教学重点
最简二次根式的运用。
教学难点
判断二次根式是否是最简二次根式和二次根式的乘除混合运算。
教学方法与资源
教学流程
备注
(一)复习回顾
1、化简(1)= (2)= (3) = (4)= (5)=
2、结合上题的计算结果,回顾前两节中利用积、商的算术平方根的性质化简二次根式达到的要求是什么?
(二)自主学习
观察上面计算题1的最后结果,可以发现这些式子中的二次根式有如下两个特点:
1.被开方数不含分母;
2.被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
2、化简:
(1) (2) (3) (4)
(三)合作交流
1、计算:
2、比较下列数的大小
(1)与 (2)
注:1、化简二次根式的方法有多种,比较常见的是运用积、商的算术平方根的性质和分母有理化。
2、判断是否为最简二次根式的两条标准:
(1)被开方数不含分母;
(2)被开方数中所有因数或因式的幂的指数都小于2.
(四)拓展延伸
观察下列各式,通过分母有理化,把不是最简二次根式的化成最简二次根式:
,
,
同理可得: =,……
从计算结果中找出规律,并利用这一规律计算
(……+)()的值.
(五)达标测试:
1、选择题
(1)如果(y>0)是二次根式,化为最简二次根式是( ).
A.(y>0) B.(y>0) C.(y>0) D.以上都不对
(2)化简二次根式的结果是
A、 B、- C、 D、-
2、填空:
(1)化简=_________.(x≥0)
(2)已知,则的值等于__________.
3、计算:
(1) (2)
板书设计
教学反思
初中人教版16.2 二次根式的乘除教案设计: 这是一份初中人教版16.2 二次根式的乘除教案设计,共9页。
2020-2021学年16.2 二次根式的乘除教案及反思: 这是一份2020-2021学年16.2 二次根式的乘除教案及反思,共5页。教案主要包含了教学目标,教学重难点,教学过程,作业布置与教学反思等内容,欢迎下载使用。
数学八年级下册16.2 二次根式的乘除教案: 这是一份数学八年级下册16.2 二次根式的乘除教案,共8页。













