贵州季期第三实验学校2023-2024学年九年级数学第一学期期末质量检测模拟试题含答案

这是一份贵州季期第三实验学校2023-2024学年九年级数学第一学期期末质量检测模拟试题含答案，共8页。试卷主要包含了下列事件中，必然事件是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．关于反比例函数，下列说法正确的是（ ）
A．点在它的图象上B．它的图象经过原点
C．当时，y随x的增大而增大D．它的图象位于第一、三象限
2．电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事，一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，前三天累计票房收入达10亿元，若设增长率为，则可列方程为（ ）
A．B．
C．D．
3．下列事件中是随机事件的个数是（ ）
①投掷一枚硬币，正面朝上；
②五边形的内角和是540°；
③20件产品中有5件次品，从中任意抽取6件，至少有一件是次品；
④一个图形平移后与原来的图形不全等．
A．0B．1C．2D．3
4．如图，已知四边形是平行四边形，下列结论不正确的是（ ）
A．当时，它是矩形B．当时，它是菱形
C．当时，它是菱形D．当时，它是正方形
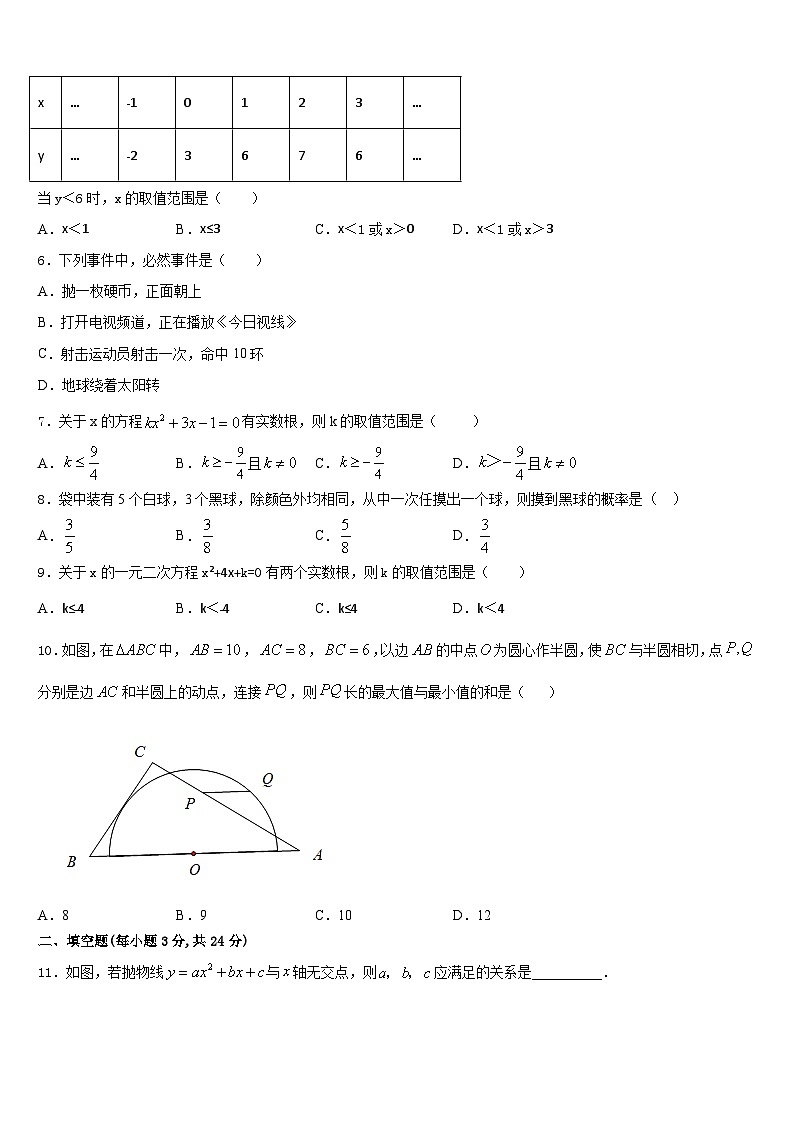
5．已知二次函数y=ax2+bx+c（a≠0），函数y与自变量x的部分对应值如下表所示：
当y＜6时，x的取值范围是（ ）
A．x＜1B．x≤3C．x＜1或x＞0D．x＜1或x＞3
6．下列事件中，必然事件是（ ）
A．抛一枚硬币，正面朝上
B．打开电视频道，正在播放《今日视线》
C．射击运动员射击一次，命中10环
D．地球绕着太阳转
7．关于x的方程有实数根，则k的取值范围是（ ）
A．B．且C．D．且
8．袋中装有5个白球，3个黑球，除颜色外均相同，从中一次任摸出一个球，则摸到黑球的概率是（ ）
A．B．C．D．
9．关于x的一元二次方程x2+4x+k=0有两个实数根，则k的取值范围是（ ）
A．k≤﹣4B．k＜﹣4C．k≤4D．k＜4
10．如图，在中，，，，以边的中点为圆心作半圆，使与半圆相切，点分别是边和半圆上的动点，连接，则长的最大值与最小值的和是（ ）
A．8B．9C．10D．12
二、填空题(每小题3分,共24分)
11．如图，若抛物线与轴无交点，则应满足的关系是__________．
12．把方程2x2﹣1=x（x+3）化成一般形式是_________.
13．小杰在楼下点A处看到楼上点B处的小明的仰角是42度，那么点B处的小明看点A处的小杰的俯角等于_____度．
14．已知，二次函数的图象如图所示，当y＜0时，x的取值范围是________．
15．把抛物线向左平移2个单位长度再向下平移3个单位长度后所得到的抛物线的函数表达式是__________．
16．已知：中，点是边的中点，点在边上，，，若以，，为顶点的三角形与相似，的长是____.
17．某厂一月份的总产量为500吨，通过技术更新，产量逐月提高，三月份的总产量达到720吨．若平均每月增长率是，则可列方程为__．
18．如图,是正三角形，D、E分别是BC、AC 上的点，当=_______时，~.
三、解答题(共66分)
19．（10分）4月23日，为迎接“世界读书日”，某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会，规则为：一个不透明的袋子中装有4个小球，小球上分别标有数字1，2，3，4，它们除所标数字外完全相同，摇匀后同时从中随机摸出两个小球，则两球所标数字之和与奖励的购书券金额的对应关系如下：
（1）通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率；
（2）书城规定：如果顾客不愿意参加摸奖，那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中，你认为哪种方式对顾客更合算？请通过求平均教的方法说明理由.
20．（6分）如图，在中，点在斜边上，以为圆心，为半径作圆，分别与、相交于点、，连接，已知.
（1）求证：是的切线；
（2）若，，求劣弧与弦所围阴影图形的面积；
（3）若，，求的长.
21．（6分）如图，学校操场旁立着一杆路灯（线段OP）．小明拿着一根长2m的竹竿去测量路灯的高度，他走到路灯旁的一个地点A竖起竹竿（线段AE），这时他量了一下竹竿的影长AC正好是1m，他沿着影子的方向走了4m到达点B，又竖起竹竿（线段BF），这时竹竿的影长BD正好是2m，请利用上述条件求出路灯的高度．
22．（8分）用配方法把二次函数y=﹣2x2+6x+4化为y=a（x+m）2+k的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．
23．（8分）（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE，求证：CE＝CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用（1）的结论证明：GE＝BE＋GD；
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE=10, 求直角梯形ABCD的面积．
24．（8分）如图，一块三角形的铁皮，边为，边上的高为，要将它加工成矩形铁皮，使它的的一边在上，其余两个顶点、分别在、上，
（1）若四边形是正方形，那么正方形边长是多少？
（2）在矩形EFGH中，设，，
①求与的函数关系，并求出自变量的取值范围；
②取多少时，有最大值，最大值是多少？
25．（10分）如图1，抛物线与x轴交于A，B两点（点A位于点B的左侧），与y轴负半轴交于点C，若AB＝1．
（1）求抛物线的解析式；
（2）如图2，E是第三象限内抛物线上的动点，过点E作EF∥AC交抛物线于点F，过E作EG⊥x轴交AC于点M，过F作FH⊥x轴交AC于点N，当四边形EMNF的周长最大值时，求点E的横坐标；
（3）在x轴下方的抛物线上是否存在一点Q，使得以Q、C、B、O为顶点的四边形被对角线分成面积相等的两部分？如果存在，求点Q的坐标；如果不存在，请说明理由．
26．（10分）如图，在平面直角坐标系中，的顶点坐标分别为（每个方格的边长均为个单位长度）.
（1）将以点为旋转中心，逆时针旋转度得到，请画出；
（2）请以点为位似中心，画出的位似三角形，使相似比为.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、D
3、C
4、D
5、D
6、D
7、C
8、B
9、C
10、C
二、填空题(每小题3分,共24分)
11、
12、x2﹣3x﹣1=1
13、1
14、
15、
16、4或
17、
18、60°
三、解答题(共66分)
19、（1）；（2）在“参加摸球”和“直接获得购书券”两种方式中，我认为选择“参加摸球”对顾客更合算，理由见解析.
20、（1）见解析；（2）；（3）
21、1m高
22、开口向下，对称轴为直线，顶点
23、（1）证明见解析；（2）证明见解析；（3）1.
24、（1）48mm；（2）①；②x=40，S的最大值是2400.
25、（1）；见解析；（2）；见解析；（3）存在，点Q的坐标为：（﹣1，﹣1）或（﹣，﹣）或（，）；详解解析．
26、（1）见详解；（2）见详解.
x
…
﹣1
0
1
2
3
…
y
…
﹣2
3
6
7
6
…
两球所标数字之和
3
4
5
6
7
奖励的购书券金额（元）
0
0
30
60
90