2023-2024学年贵州季期第三实验学校数学八上期末检测模拟试题含答案

这是一份2023-2024学年贵州季期第三实验学校数学八上期末检测模拟试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，已知则a、b、c的大小关系是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。答案不能答在试题卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。不按以上要求作答无效。
4．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．某小组长统计组内1人一天在课堂上的发言次数分别为3，3，0，4，1．关于这组数据，下列说法错误的是（ ）
A．众数是3B．中位数是0C．平均数3D．方差是2.8
2．如图，在△ABC中，D、E分别是AB、AC的中点，BC=16，F是DE上一点，连接AF、CF，DE=4DF，若∠AFC=90°，则AC的长度为（ ）
A．11B．12C．13D．14
3．某市道路改造中，需要铺设一条长为1200米的管道，为了尽量减少施工对交通造成的影响，实际施工时，工作效率比原计划提高了25%，结果提前了8天完成任务．设原计划每天铺设管道x米，根据题意，则下列方程正确的是（ ）
A． B．
C．D．
4．一个正数的两个平方根分别是2a-1与-a+2，则a的值为（ ）
A．1B．-1C．2D．-2
5．将点A(2，1)向右平移2个单位长度得到点A′，则点A′的坐标是（ ）
A．(0，1)B．(2，﹣1)C．(4，1)D．(2，3)
6．已知则a、b、c的大小关系是（）
A．a＞b＞cB．b＞a＞cC．c＞a＞bD．b＞c＞a
7．一个多边形截去一个角后，形成另一个多边形的内角和为，那么原多边形的边数为（ ）
A．5B．5或6C．6或7或8D．7或8或9
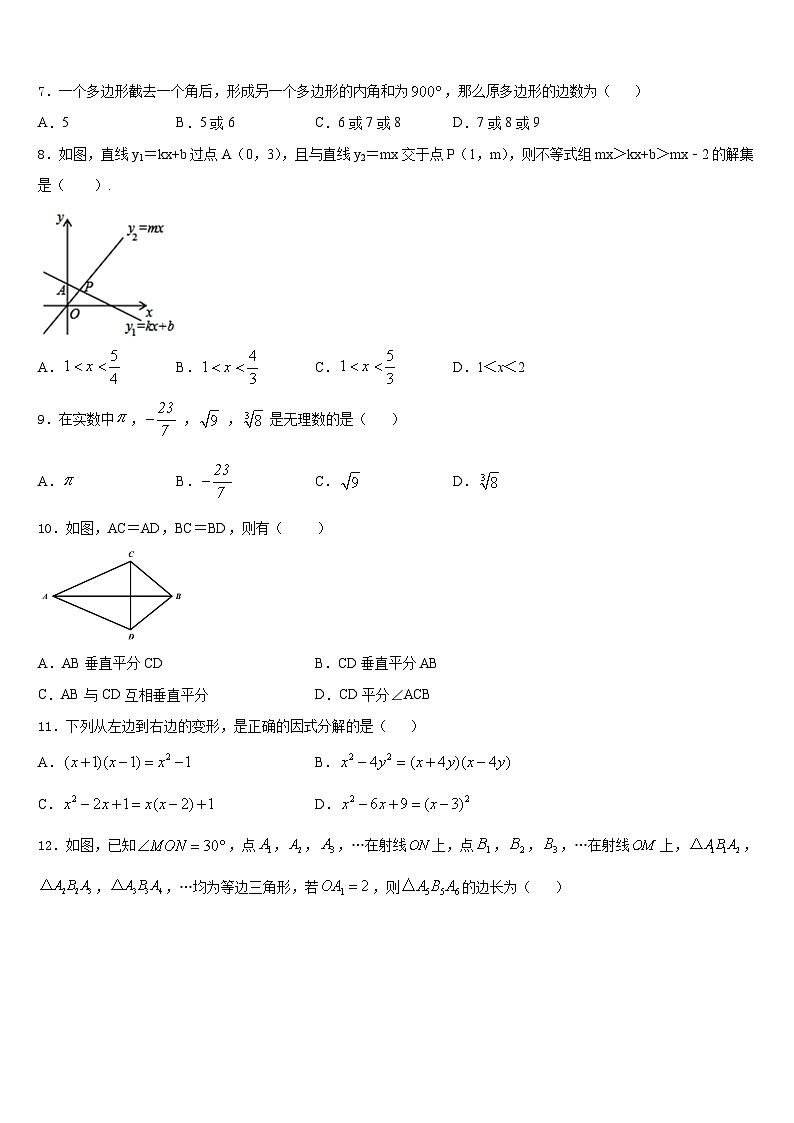
8．如图，直线y1＝kx+b过点A（0，3），且与直线y2＝mx交于点P（1，m），则不等式组mx＞kx+b＞mx﹣2的解集是（ ）.
A．B．C．D．1＜x＜2
9．在实数中， ， ， 是无理数的是（ ）
A．B．C．D．
10．如图，AC＝AD，BC＝BD，则有（ ）
A．AB垂直平分CDB．CD垂直平分AB
C．AB与CD互相垂直平分D．CD平分∠ACB
11．下列从左边到右边的变形，是正确的因式分解的是（ ）
A．B．
C．D．
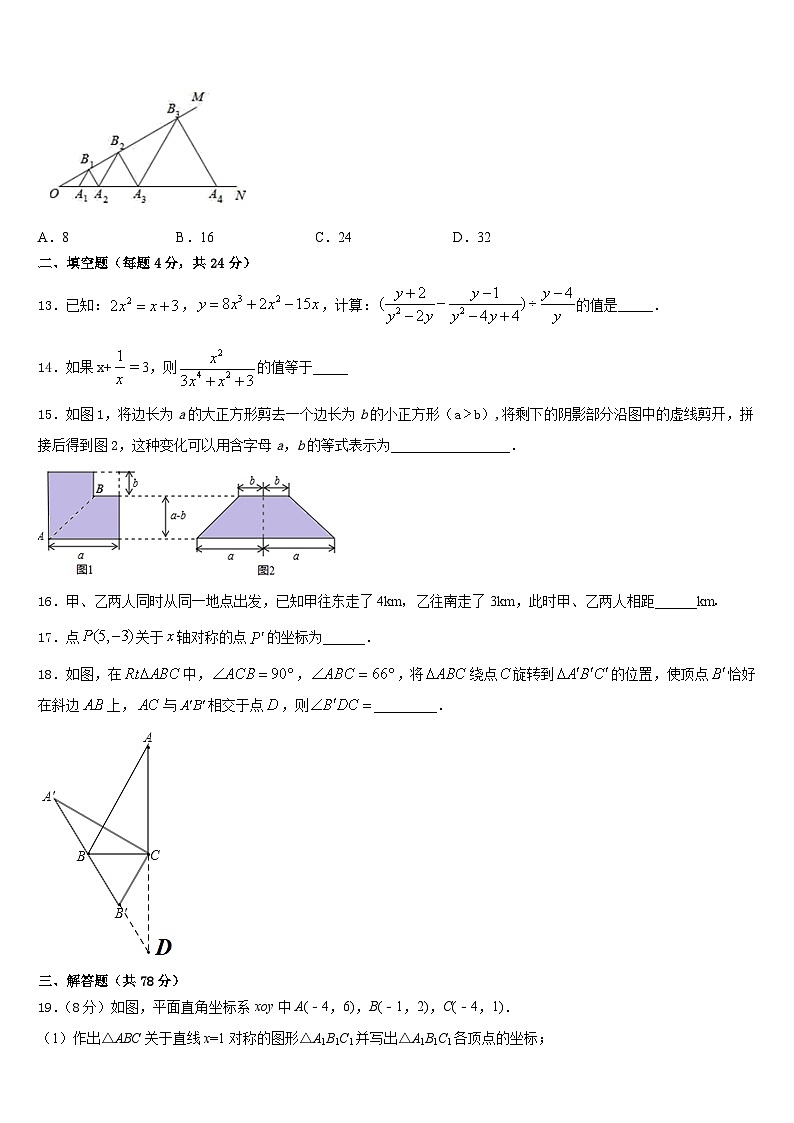
12．如图，已知，点，，，…在射线上，点，，，…在射线上，，，，…均为等边三角形，若，则的边长为（ ）
A．8B．16C．24D．32
二、填空题（每题4分，共24分）
13．已知：，，计算：的值是_____．
14．如果x+＝3，则的值等于_____
15．如图1，将边长为a的大正方形剪去一个边长为b的小正方形（ab）,将剩下的阴影部分沿图中的虚线剪开，拼接后得到图2，这种变化可以用含字母a，b的等式表示为_________________．
16．甲、乙两人同时从同一地点出发，已知甲往东走了4km，乙往南走了3km，此时甲、乙两人相距______km．
17．点关于轴对称的点的坐标为______．
18．如图，在中，，，将绕点旋转到的位置，使顶点恰好在斜边上，与相交于点，则_________．
三、解答题（共78分）
19．（8分）如图，平面直角坐标系xy中A(﹣4，6)，B(﹣1，2)，C(﹣4，1)．
（1）作出△ABC关于直线x=1对称的图形△A1B1C1并写出△A1B1C1各顶点的坐标；
（2）将△A1B1C1向左平移2个单位，作出平移后的△A2B2C2，并写出△A2B2C2各顶点的坐标；
（3）观察△ABC和△A2B2C2，它们是否关于某直线对称？若是，请指出对称轴，并求△ABC的面积．
20．（8分）如图，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：
（1）PC＝ cm．（用t的代数式表示）
（2）当t为何值时，△ABP≌△DCP？
（3）当点P从点B开始运动，同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．
21．（8分）在边长为1的小正方形网格中，的顶点均在格点上，
（1）点关于轴的对称点坐标为；
（2）将向左平移3个单位长度得到，请画出，求出的坐标；
（3）求出的面积．
22．（10分）南京市某花卉种植基地欲购进甲、乙两种兰花进行培育，每株甲种兰花的成本比每株乙种兰花的成本多100元，且用1200元购进的甲种兰花与用900元购进的乙种兰花数量相同．
（1）求甲、乙两种兰花每株成本分别为多少元？
（2）该种植基地决定在成本不超过30000元的前提下培育甲、乙两种兰花，若培育乙种兰花的株数比甲种兰花的3倍还多10株，求最多购进甲种兰花多少株？
23．（10分）某公司销售部有营销员15人，销售部为了制定关于某种商品的每位营销员的个人月销售定额，统计了这15人某月关于此商品的个人月销售量（单位：件）如下：
（1）求这15位营销员该月关于此商品的个人月销售量的平均数，并直接写出这组数据的中位数和众数；
（2）假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件，你认为对多数营销员是否合理？并在（1）的基础上说明理由．
24．（10分）解下列分式方程：
（1）
（2）．
25．（12分）如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为______；
（2）当△PMN所放位置如图②所示时，求证：∠PFD−∠AEM＝90°；
（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．
26．（12分）甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：
根据以上信息，整理分析数据如下：
（1）求出表格中，，的值；
（2）分别运用上表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？
参考答案
一、选择题（每题4分，共48分）
1、B
2、B
3、B
4、B
5、C
6、B
7、C
8、C
9、A
10、A
11、D
12、D
二、填空题（每题4分，共24分）
13、．
14、
15、
16、5
17、（5，3）
18、24°
三、解答题（共78分）
19、（1）作图见解析，A1(6，6)，B1(3，2)，C1(6，1)；（2）作图见解析，A2(4，6)，B2(1，2)，C2(4，1)；（3）△ABC和△A2B2C2关于y轴对称，△ABC的面积=7.1．
20、（1）(10﹣2t)；（2）t＝2.5；（3）2.4或2
21、（1）点关于轴的对称点坐标为； （2）图详见解析，的坐标为；（3）
22、（1）每株甲种兰花的成本为400元，每株乙种兰花的成本为300元；（2）最多购进甲种兰花20株．
23、（1）平均数320，中位数210，众数210；（2）不合理，理由见解析．
24、（1）无解；（2）
25、（1）∠PFD＋∠AEM=90°；（2）见解析；（3）45°
26、（1）a=7，b=7.5，c=1.2；（2）选甲，理由见解析
个人月销售量
1800
510
250
210
150
120
营销员人数
1
1
3
5
3
2
平均成绩/环
中位数/环
众数/环
方差
甲
8
乙
7
7
7