



- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题01 集合及其运算(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题04 函数的概念及表示(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题05 函数的基本性质(12大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
- 【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题06 幂指对函数的图象与性质(10大考点,知识串讲+热考题型+专题训练)- 试卷 0 次下载
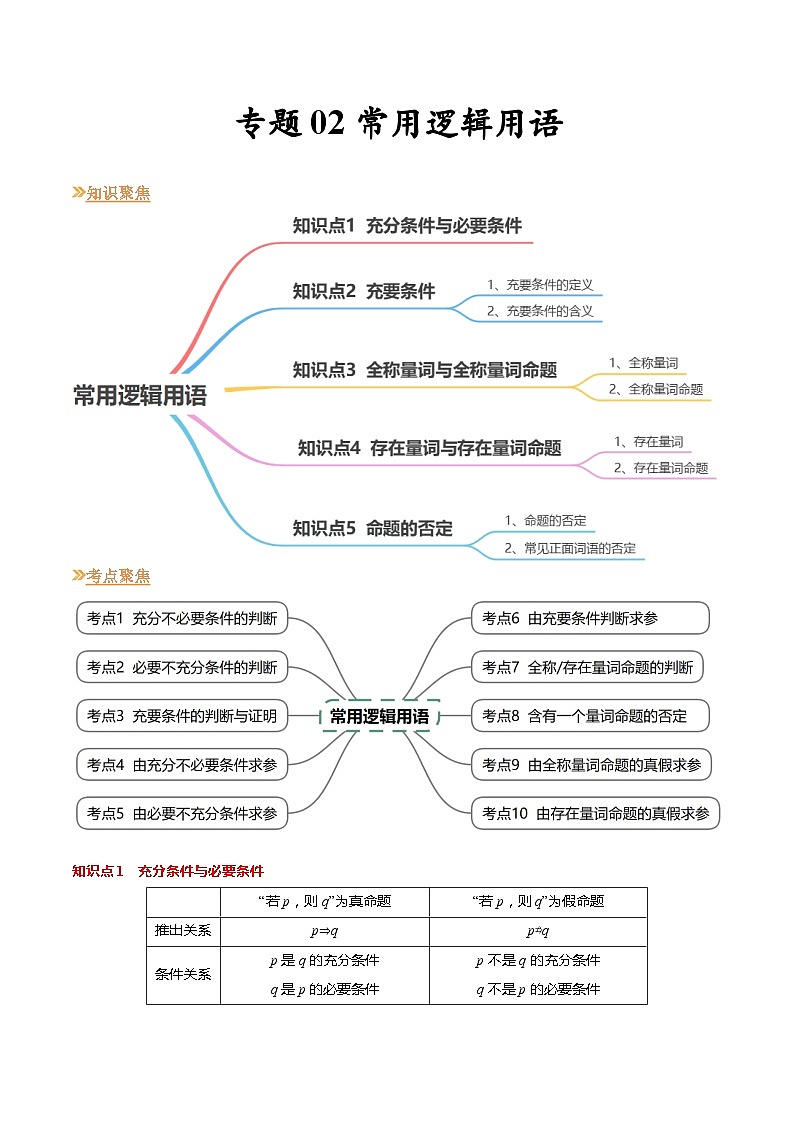
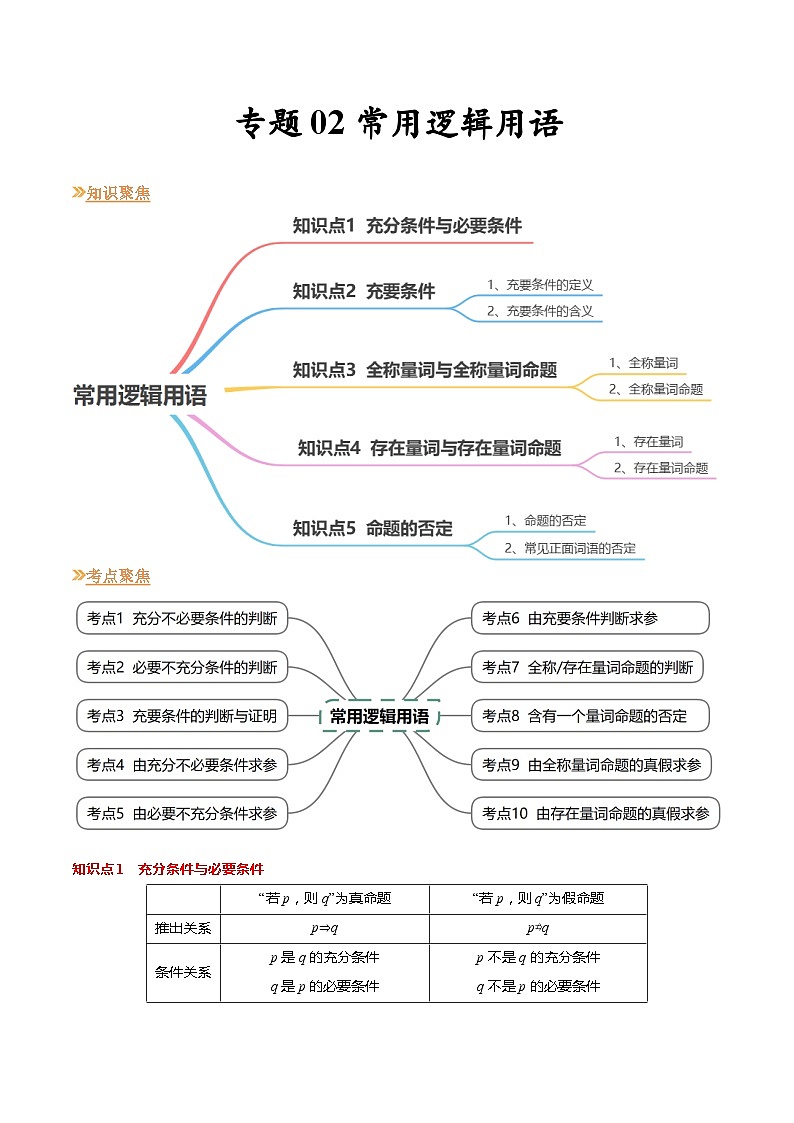
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 常用逻辑用语(10大考点,知识串讲+热考题型+专题训练)-
展开知识聚焦
考点聚焦
知识点1 充分条件与必要条件
【注意】
(1)前提p⇒q,有方向,条件在前,结论在后;
(2)p是q的充分条件或q是p的必要条件;
(3)改变说法:“p是q的充分条件”还可以换成q的一个充分条件是p;
“q是p的必要条件”还可以换成“p的一个必要条件是q”.
知识点2 充要条件
1、充要条件的定义
如果“若,则”和它的逆命题“若,则”均为真命题,即既有,又有,就记作。
此时,既是的充分条件,也是的必要条件,我们说是的充分必要条件,简称充要条件。
2、充要条件的含义
若是的充要条件,则也是的充要条件,虽然本质上是一样的,但在说法上还是不同的,
因为这两个命题的条件与结论不同。
3、充要条件的等价说法:是的充要条件又常说成是成立当且仅当成立,或与等价。
知识点3 全称量词与全称量词命题
1、全称量词:短语“所有的”“任意一个”在逻辑中通常叫作全称量词,并用符号“”表示.
【注意】(1)全称量词的数量可能是有限的,也可能是无限的,由有题目而定;
(2)常见的全称量词还有“一切”、“任给”等,相应的词语是“都”
2、全称量词命题
(1)定义:含有全称量词的命题,称为全称量词命题.
(2)符号表示:通常,将含有变量的语句用,,,…表示,变量的取值范围用表示,那么,全称量词命题“对中任意一个,成立”可用符号简记为
【注意】(1)从集合的观点看,全称量词命题是陈述某集合中所有元素都具有某种性质的命题;
(2)一个全称量词命题可以包含多个变量;
(3)有些全称量词命题中的全称量词是省略的,理解时需要把它补出来。
如:命题“平行四边形对角线互相平行”理解为“所有平行四边形对角线都互相平行”。
知识点4 存在量词与存在量词命题
1、存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫作存在量词,并用符号“”表示.
【注意】常见的存在量词还有“有些”、“有一个”、“对某些”、“有的”等;
2、存在量词命题
(1)定义:含有存在量词的命题,叫作存在量词命题。
(2)符号表示:存在量词命题“存在中的元素,使成立”可用符号简记为
【注意】(1)从集合的观点看,存在量词命题是陈述某集合中有一些元素具有某种性质的命题;
(2)一个存在量词命题可以包含多个变量;
(3)有些命题虽然没有写出存在量词,但其意义具备“存在”、“有一个”等特征都是存在量词命题
知识点5 命题的否定
1、命题的否定:对命题p加以否定,得到一个新的命题,记作“”,读作“非p”或p的否定.
(1)全称量词命题的否定:
一般地,全称量词命题“”的否定是存在量词命题: .
(2)存在量词命题的否定:
一般地,存在量词命题“ ”的否定是全称量词命题: .
2、常见正面词语的否定:
考点剖析
考点1 充分不必要条件的判断
【例1】(2023春·江西宜春·高一校联考期中)“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【变式1-1】(2023秋·四川南充·高一校考阶段练习)对于实数,或,那么是的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
【变式1-2】(2023秋·宁夏银川·高一银川一中校考阶段练习)设计如图所示的四个电路图,条件:“开关闭合”;条件:“灯泡亮”,则是的充分不必要条件的电路图是( )
A.(1) B.(2) C.(3) D.(4)
【变式1-3】(2023秋·重庆·高一校考阶段练习)(多选)已知p:,则p的充分不必要条件有( )
A. B. C. D.
【变式1-4】(2023秋·安徽亳州·高一校考阶段练习)(多选)已知,,则“”是真命题的一个充分不必要条件是( )
A. B. C. D.
考点2 必要不充分条件的判断
【例2】(2023秋·安徽合肥·高一校联考期末)已知p:,q:,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充分条件 D.既不充分又不必要条件
【变式2-1】(2022秋·湖北鄂州·高一校联考期中)设,则“”是“”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
【变式2-2】(2023秋·山西运城·高一校考阶段练习)设,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【变式2-3】(2023秋·北京·高一校考阶段练习)荀子曰:“故不积跬步,无以至千里;不积小流,无以成江海.”这句来自先秦时期的名言阐述了做事情不一点一点积累,就永远无法达成目标的哲理.由此可得,“积跬步”是“至千里”的( )
A.充分条件 B.必要条件 C.充要条件 D.既不充分也不必要条件
【变式2-4】(2023·陕西榆林·高一校考阶段练习)(多选)命题p:的必要不充分条件是( )
A. B. C. D.
考点3 充要条件的判断与证明
【例3】(2023·江苏·高一专题练习)点是第二象限的点的充要条件是( )
A. B. C. D.
【变式3-1】(2023·江苏·高一专题练习)“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【变式3-2】(2022秋·福建泉州·高一统考期中)已知实数x,y,则“”是“”的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
【变式3-3】(2023·高一课时练习)(多选)设全集为,在下列条件中,是的充要条件的为( )
A. B. C. D.
【变式3-4】(2023·全国·高一专题练习)设集合,若集合,,则的充要条件是( )
A., B., C., D.,
考点4 由充分不必要条件求参
【例4】(2022秋·河南商丘·高一校考阶段练习)已知p:或,q:,则a取下面那些范围,可以使q是p的充分不必要条件( )
A. B. C. D.
【变式4-1】(2023秋·甘肃武威·高一校考阶段练习)已知不等式成立的一个充分不必要条件是,则实数m的取值范围是 .
【变式4-2】(2023秋·北京·高一校考阶段练习)已知表示不大于的最大整数,,,若是的充分不必要条件,则的取值范围是 .
【变式4-3】(2023秋·四川南充·高一校考阶段练习)已知集合,.
(1)当时,求;
(2)是的充分不必要条件,求实数的取值范围.
【变式4-4】(2022秋·湖北荆州·高一校考阶段练习)已知全集,集合,
(1)若,求;
(2)若“”是“”的充分不必要条件,求实数的取值范围.
考点5 由必要不充分条件求参
【例5】(2023秋·全国·高一专题练习)设,,若是的必要不充分条件,则实数的取值范围是( )
A. B. C. D.
【变式5-1】(2022秋·福建福州·高一校考期中)已知的必要不充分条件是或,则实数的最大值为 .
【变式5-2】(2023秋·重庆铜梁·高一校考阶段练习)已知,.
(1)当时,求;
(2)若“”是“”的必要不充分条件,求实数a的取值范围.
【变式5-3】(2023·全国·高一专题练习)已知集合,.
(1)若,求实数k的取值范围;
(2)已知命题,命题,若p是q的必要不充分条件,求实数k的取值范围.
【变式5-4】(2021秋·高一课时练习)已知方程在上有解.
(1)求实数的取值集合;
(2)设不等式的解集为,若是的必要条件,求a的取值范围.
考点6 由充要条件判断求参
【例6】(2022秋·福建宁德·高一统考期中)“不等式在上恒成立”的充要条件是( )
A. B. C. D.或
【变式6-1】(2023·江苏·高一专题练习)若“不等式成立”的充要条件为“”,则实数的值为 .
【变式6-2】(2023·江苏·高一专题练习)设集合,;
(1)用列举法表示集合;
(2)若是的充要条件,求实数的值.
【变式6-3】(2023·全国·高一专题练习)已知方程,求使方程有两个大于的实数根的充要条件.
【变式6-4】(2023·全国·高一专题练习)方程与有一个公共实数根的充要条件是( ).
A. B. C. D.
考点7 全称/存在量词命题的判断
【例7】(2023秋·贵州遵义·高一校考阶段练习)判断下列命题是存在量词命题的个数( )
①每一个一次函数都是增函数;
②至少有一个自然数小于1;
③存在一个实数x,使得;
④两直线平行,内错角相等.
A.1个 B.2个 C.3个 D.4个
【变式7-1】(2023秋·全国·高一专题练习)下列全称量词命题为真命题的是( )
A.所有的质数都是奇数
B.,
C.对每一个无理数,也是无理数
D.所有能被5整除的整数,其末位数字都是5
【变式7-2】(2023秋·全国·高一专题练习)下列命题中,是真命题且是全称命题的是( )
A.对任意实数a,b,都有
B.梯形的对角线不相等
C.
D.所有的集合都有子集
【变式7-3】(2023秋·辽宁大连·高一校考阶段练习)(多选)设非空集合满足,且,则下列选项中错误的是( )
A.,有 B.,使得
C.,使得 D.,有
考点8 含有一个量词命题的否定
【例8】(2022秋·黑龙江佳木斯·高一校考期中)命题“,”的否定是( )
A., B.,
C., D.,
【变式8-1】(2023春·海南·高一校考期中)全称量词命题:“{能被整除的整数},是偶数.”的否定是( )
A.{能被整除的整数},不是偶数
B.{能被整除的整数},不是偶数
C.{能被整除的整数},是偶数.
D.{能被整除的整数},不是偶数.
【变式8-2】(2023秋·吉林辽源·高一校联考期末)命题“,使”的否定是( )
A.,使 B.不存在,使
C.,使 D.,使
【变式8-3】(2023秋·山西运城·高一校考阶段练习)命题“”的否定是( )
A. B.
C. D.
【变式8-4】(2023秋·湖北荆州·高一校考阶段练习)命题“,有实数解”的否定是( )
A.,有实数解 B.,无实数解
C.,无实数解 D.,有实数解
考点9 由全称量词命题的真假求参
【例9】(2023秋·湖北宜昌·高一校考阶段练习)“,”为真命题,则实数的取值范围为( )
A. B. C. D.
【变式9-1】(2022秋·云南红河·高一校考阶段练习)若,为真命题,则的取值范围为( )
A. B. C. D.
【变式9-2】(2023秋·贵州黔东南·高一校考阶段练习)(多选)若“,都有”是真命题,则实数可能的值是( )
A.1 B. C.3 D.
【变式9-3】(2022秋·四川绵阳·高一校考阶段练习)若命题“对任意的,恒成立”为假命题,则m的取值范围为( )
A. B. C. D.
【变式9-4】(2023秋·陕西榆林·高一校考阶段练习)命题:“,”为假命题,则的取值范围为 .
考点10 由存在量词命题的真假求参
【例10】(2023秋·河南许昌·高一校考阶段练习)若命题p:是真命题,则实数m的取值范围是( )
A. B. C. D.
【变式10-1】(2023秋·全国·高一专题练习)已知命题:,使得成立为真命题,则实数的取值范围是( )
A. B. C. D.
【变式10-2】(2023秋·四川南充·高一校考阶段练习)若“,使得成立”是假命题,则实数的取值范围为( )
A. B. C. D.
【变式10-3】(2023秋·吉林长春·高一校考阶段练习)“”是假命题,则实数的取值范围为( )
A. B. C. D.
【变式10-4】(2023秋·吉林长春·高一东北师大附中校考阶段练习)命题“”为假命题,则实数的取值范围是 .
过关检测
1.(2023秋·甘肃临夏·高一校考期末)命题“,”的否定为( )
A., B.,
C., D.,
2.(2023秋·四川南充·高一校考阶段练习)已知集合,,则“”是“”的( )
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分又不必要条件
3.(2023秋·山东菏泽·高一校考阶段练习)王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其《从军行》传诵至今,“青海长云暗雪山,孤城遥望玉门关. 黄沙百战穿金甲,不破楼兰终不还”,由此推断,其中最后一句“攻破楼兰”是“返回家乡”的( )
A.必要条件 B.充分条件 C.充要条件 D.既不充分又不必要条件
4.(2023·全国·高一专题练习)使成立的一个充分不必要条件是( )
A. B. C. D.
5.(2023秋·全国·高一专题练习)已知是的充分条件,是的充分不必要条件,是的必要条件,是的必要条件,现有下列命题:①是的必要不充分条件;②是的充分不必要条件;③是的充分不必要条件;④是的充要条件.正确的命题序号是( )
A.① B.② C.③ D.④
6.(2023春·江西宜春·高一校联考期中)若,使得成立是假命题,则实数可能取值是( )
A. B. C.4 D.5
7.(2023秋·湖北荆州·高一沙市中学校考阶段练习)已知命题:命题:R,,若命题,都是真命题,实数的取值范围是( )
A. B. C.或 D.
8.(2023·全国·高一专题练习)(多选)下列选项中p是q的必要不充分条件的有( )
A.p:,q:
B.p:,q:
C.p:两个三角形全等,q:两个三角形面积相等
D.p:,q:
9.(2023·全国·高一专题练习)(多选)下列命题不正确的是( )
A.,
B.,
C.“”的充要条件是“”
D.“,”是“”的充分条件
10.(2023秋·重庆合川·高一校考阶段练习)(多选)已知命题;命题:若恒成立,则.则( )
A.的否定是假命题 B.的否定是真命题
C.与都为假命题 D.与都为真命题
11.(2023秋·江苏南京·高一南京市中华中学校考阶段练习)命题“,”的否定是 .
12.(2022秋·河南商丘·高一校考阶段练习)若或是或的必要不充分条件,则实数的取值范围是 .
13.(2023·全国·高一专题练习)方程 有一正一负根的充要条件是
14.(2023·全国·高一专题练习)已知全集,集合,.
(1)若,求;
(2)若“”是“”充分不必要条件,求实数a的取值范围.
15.(2023秋·贵州六盘水·高一校考阶段练习)(1)已知,若是的必要不充分条件,求实数的取值范围;
(2)已知,若是的充分条件,求实数的取值范围.“若p,则q”为真命题
“若p,则q”为假命题
推出关系
p⇒q
p⇏q
条件关系
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
定理关系
判定定理给出了相应数学结论成立的充分条件
性质定理给出了相应数学结论成立的必要条件
正面词语
等于(=)
大于(>)
小于(<)
是
都是
否定
不等式(≠)
不大于(≤)
不小于(≥)
不是
不都是
正面词语
至多有一个
至少有一个
任意
所有
至多有n个
否定
至少有两个
一个都没有
某个
某些
至少有n+1个
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题11+余弦定理(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题11余弦定理6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 向量的数乘(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题03向量的数乘6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 向量的加减法(6大考点,知识串讲+热考题型+专题训练)-讲义: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题02 向量的加减法(6大考点,知识串讲+热考题型+专题训练)-讲义,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题02向量的加减法6大考点知识串讲+热考题型+专题训练原卷版docx、寒假作业苏教版2019高中数学高一寒假提升训练专题02向量的加减法6大考点知识串讲+热考题型+专题训练解析版docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。