广东省广州市越秀区2023-2024学年九年级上学期期末数学试题(无答案)

这是一份广东省广州市越秀区2023-2024学年九年级上学期期末数学试题(无答案)，共7页。试卷主要包含了 考生必须保证答题卡的整洁等内容，欢迎下载使用。

本调研卷共6页，25小题，满分120分. 建议完成时间：120分钟.
注意事项：
1. 答卷前，考生务必将自己的姓名、考生号、试室号和座位号填写在答题卡上.
2. 用2B铅笔将考生号、座位号等填涂在答题卡相应位置上. 作答选择题时，选出每小题答案后，用2B铅笔将答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案. 答案不能答在试卷上.
3. 非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液、涂改带. 不按以上要求作答无效.
4. 考生必须保证答题卡的整洁. 考试结束后，将试卷和答题卡一并交回.
第一部分 选择题（共30分）
一、选择题（本大题共有10小题，每小题3分，满分30分. 在每小题给出的四个选项中，只有一项是符合题目要求的. ）
1. 下列图形中，是中心对称图形的是（ ）.
A. B. C. D.
2. 抛物线的顶点坐标是（ ）.
A. B. C. D.
3. 用配方法解一元二次方程的过程中，配方正确的是（ ）.
A. B.
C. D.
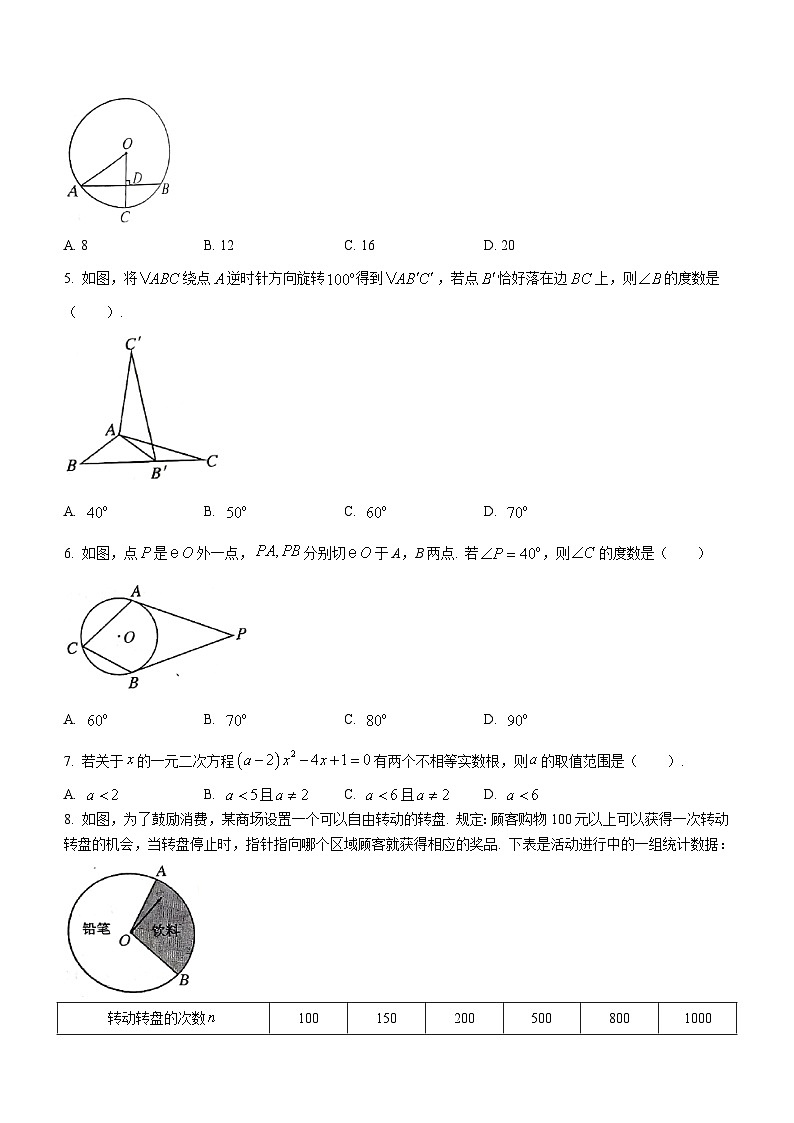
4. 如图，是半径，是的弦，且于点. 若，则弦的长是（ ）.
A. 8B. 12C. 16D. 20
5. 如图，将绕点逆时针方向旋转得到，若点恰好落在边上，则的度数是（ ）.
A. B. C. D.
6. 如图，点是外一点，分别切于A，B两点. 若，则的度数是（ ）
A. B. C. D.
7. 若关于的一元二次方程有两个不相等实数根，则的取值范围是（ ）.
A. B. 且C. 且D.
8. 如图，为了鼓励消费，某商场设置一个可以自由转动的转盘. 规定：顾客购物100元以上可以获得一次转动转盘的机会，当转盘停止时，指针指向哪个区域顾客就获得相应的奖品. 下表是活动进行中的一组统计数据：
则转盘中“饮料”区域的圆心角的度数近似是（ ）.
A. B. C. D.
9. 如图，在四边形中，且与交于点，分别是的中点，则的面积与四边形的面积比是（ ）.
A. B. C. D.
10. 如图，抛物线交轴于两点，交轴的负半轴于点，顶点为. 下列结论：
①；
②；
③若为该抛物线上两点且，则；
④若是等腰直角三角形，则；
⑤若是关于的一元二次方程的两个根，则. 其中正确的是（ ）.
A. ①②③B. ③④⑤C. ①④⑤D. ①③④
第二部分 非选择题（共90分）
二、填空题（本大题共6小题，每小题3分，满分18分. ）
11. 若是方程的一个根，则__________.
12. 在一个不透明的袋中装有3个红球，1个黑球，每个球除颜色外都相同. 从中任意摸出2球，则“摸出的球中至少有1个红球”是__________事件. （填“必然”，“不可能”或“随机”）
13. 如图，线段两个端点的坐标分别为，，以原点为位似中心，在第一象限内将线段缩小为原来的后得到线段，则点的坐标是__________.
14. 如图，在中，，以为轴将旋转一周得到一个圆锥，则该圆锥侧面展开图的扇形圆心角的度数是__________.
15. 已知二次函数的函数值和自变量的部分对应取值如下表所示：
若在这三个实数中，只有一个是正数，则的取值范围是__________.
16. 如图，在长方形中，，点为边上点，且，点为边上动点，将线段绕点顺时针旋转得到线段与边交于点，连接.
（1）当点与点重合时，的面积是__________.
（2）当点在边上运动时，的面积最小值是__________.
三、解答题（本大题共9小题，满分72分. 解答应写出文字说明、证明过程或演算步骤. ）
17. （本小题满分4分）
解方程：.
18. （本小题满分4分）
如图，已知，将绕点沿顺时针方向旋转后得到.
（1）请在图中画出；
（2）直接写出线段在旋转过程中扫过的图形面积：___________.
19. （本小题满分6分）
如图是某数学兴趣小组设计用手电筒来测量某古城墙高度的示意图，在点处放一水平的平面镜，光线从点出发经平面镜反射后刚好射到古城墙的顶端处，测得光源距离地面高度米，米，米，三点在同一水平线上，求该古城墙的高度（为法线，平面镜的厚度忽略不计）.
20. （本小题满分6分）
如图，直线分别交轴，轴于两点，经过两点的抛物线与轴的正半轴相交于点.
（1）求抛物线的解析式；
（2）结合图象，直接写出不等式的解集.
21. （本小题满分8分）
2023年举世瞩目的第十九届亚运会在中国杭州举行，亚运会吉祥物“宸宸”、“琮琮”、“莲莲”成为热销产品. 小李和小张去杭州旅游，他们分别从这三个吉祥物中任意选购一款以作留念.
（1）小李选购吉祥物“琮琮”的概率是__________；
（2）请用列表法或画树状图法，求小李和小张选购同一款吉祥物的概率.
22. （本小题满分10分）
2022年教育部正式印发《义务教育课程方案和课程标准（2022年版）》，《劳动》成为一门独立的课程. 某学校率先行动，在校园开辟了一块劳动教育基地，用一段长为30米的篱笆围成一个一边靠墙的矩形养殖园（靠墙的一边不需用篱笆），墙长为16米.
（1）当围成的矩形养殖园面积为108平方米时，求养殖园的边的长；
（2）求矩形养殖园面积的最大值.
23. （本小题满分10分）
如图，为的直径，为的弦，且，点为劣弧上一点，且，与交于点.
（1）尺规作图：作出点，并连接. （保留作图痕迹，不写作法）；
（2）连接，为延长线上一点，求证：平分；
（3）求证：.
24. （本小题满分12分）
已知抛物线与轴交于点（点在点的左侧），与轴交于点，点为轴上一动点，过点作轴的垂线交抛物线于点（与不重合）.
（1）求点的纵坐标（用含的式子表示）；
（2）当时，若，求抛物线的纵坐标在时的取值范围；
（3）对于的每一个确定的值，有最小值，若，求的取值范围.
25. （本小题满分12分）
如图，四边形中，，
（1）求的度数；
（2）连接，若，求证：；
（3）点分别为线段和上的点，点是线段上任意一点且和的面积相等，过点作交直线于点，连接. 若，求线段的最小值. 转动转盘的次数
100
150
200
500
800
1000
落在“饮料”区域次数
32
39
64
155
254
299
…
0
1
2
3
…
…
1
1
…