

广东省广州市海珠区2023-2024学年九年级上学期期末数学试题(无答案)
展开试卷分选择题和非选择题两部分,共三大题25小题,共5页,满分120分,考试时间120分钟,不可使用计算器.
注意事项:
1.答卷前,考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写自己的学校、班级、姓名、座位号、考号;再用2B铅笔把对应号码的标号涂黑.
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题号的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B铅笔画图,答案必须写在答题卡各题指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域.不准使用铅笔、圆珠笔和涂改液,不按以上要求作答的答案无效,
4.考生必须保持答题卡的整洁,考试结束后,将本试卷和答题卡一并交回.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列图形中,不是中心对称图形的是( ).
A.B.C.D.
2.若一元二次方程的两根为,,则的值是( ).
A.4B.C.2D.
3.关于二次函数下列说法正确的是( ).
A.开口向上B.对称轴是y轴
C.有最小值D.当时,函数y随x的增大而减小
4.如图,和是位似图形,点O是它们的位似中心,其中,则与的面积之比是( ).
(第4题图)
A.1:2B.2:1C.1:4D.4:1
5.用配方法解方程,下列变形正确的是( ).
A.B.C.D.
6.在中,,,,以点C为圆心,为半径作,则点A与的位置关系是( ).
A.点A在内B.点A在上C.点A在外D.无法确定
7.如图,在高3米,宽5米的矩形墙面上有一块长方形装饰板(图中阴影部分),装饰板的上面和左右两边都留有宽度相同为x米的空白墙面。若矩形装饰板的面积为4.5平方米,则以下方程正确的是( ).
(第7题图)
A.B.
C.D.
8.如图,该平面图形绕着它的中心旋转一定角度后与自身重合,则这个旋转角度可能是( ).
(第8题图)
A.B.C.D.
9.如图,的内切圆分别与、相切于D点、E点,若,,则( ).
(第9题图)
A.B.C.D.
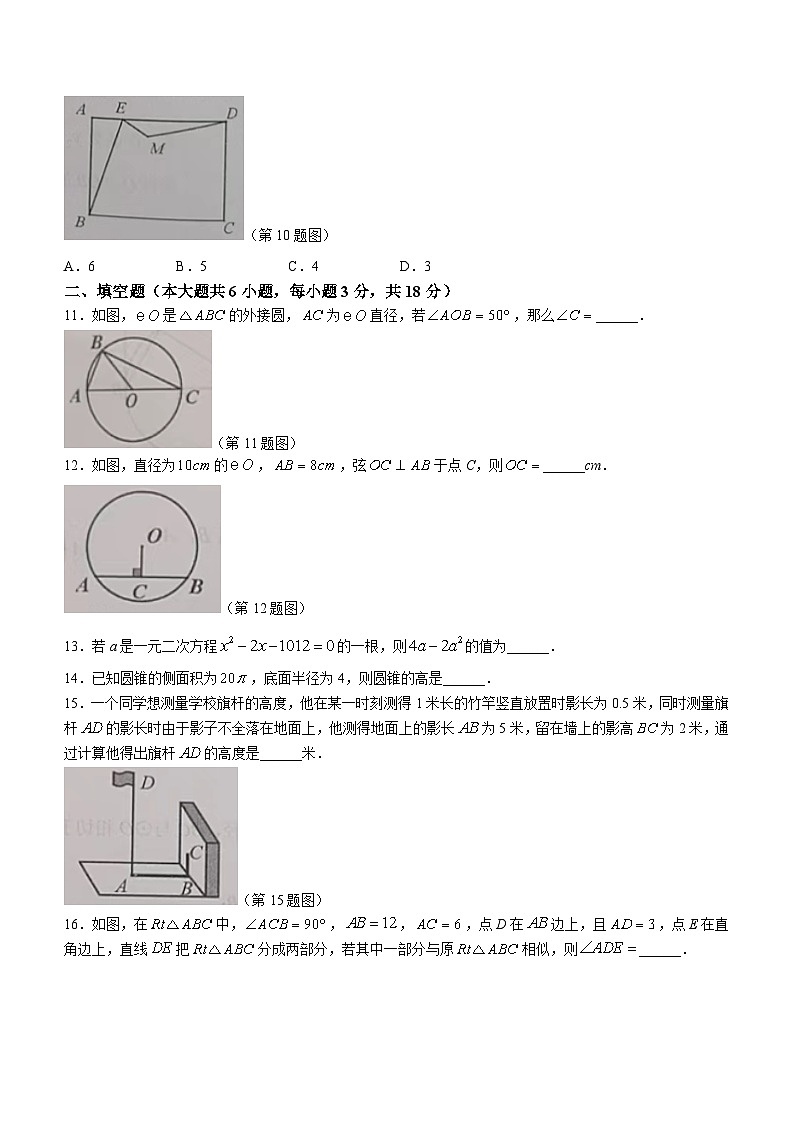
10.如图,在矩形中,,,点E是边上的动点,点M是点A关于直线的对称点,连接,则的最小值是( ).
(第10题图)
A.6B.5C.4D.3
二、填空题(本大题共6小题,每小题3分,共18分)
11.如图,是的外接圆,为直径,若,那么______.
(第11题图)
12.如图,直径为的,,弦于点C,则______cm.
(第12题图)
13.若a是一元二次方程的一根,则的值为______.
14.已知圆锥的侧面积为,底面半径为4,则圆锥的高是______.
15.一个同学想测量学校旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为0.5米,同时测量旗杆的影长时由于影子不全落在地面上,他测得地面上的影长为5米,留在墙上的影高为2米,通过计算他得出旗杆的高度是______米.
(第15题图)
16.如图,在中,,,,点D在边上,且,点E在直角边上,直线把分成两部分,若其中一部分与原相似,则______.
(第16题图)
三、解答题(本大题有9个小题,共72分,解答要求写出文字说明,证明过程或计算步骤)
17.(本题满分6分)
解方程:(1);(2).
18.(本题满分6分)
利用图中的网格线(最小的正方形的边长为1)画图.
(1)画出,使它与是关于原点O的中心对称:
(2)将绕点A逆时针旋转得到.
(第18题图)
19.(本题满分6分)
二次函数的图象如图所示,其中图象与x轴交于点A和点B.
(1)求此二次函数的解析式;
(2)直接写出不等式的解集.
第19题图
20.(本题满分6分)
已知关于x的一元二次方程有两个不等的实数根.
(1)求k的取值范围:
(2)若方程有一个根为2,求方程的另一根.
21.(本题满分6分)
如图,已知是的直径,与相切于点B,与相交于点D.
(1)求证::
(2)若,,求的长度.
第21题图
22.(本题满分8分)
某店销售一种环保建筑涂料,当每桶售价为300元时,月销售量为60桶,该店为提高经营利润,准备采取降价的方式进行促销,经市场调查发现:当该涂料每桶售价每下降5元时,月销售量就会增加10桶,每售出1桶涂料共需支付厂家及其他费用200元.
(1)当每桶售价是280元时,求此时该店的月销售量为多少桶?
(2)求每桶降价多少元时,该店能获得最大月利润?最大月利润为多少元?
23.(本题满分10分)
如图,点C在以为直径的上,点D是的中点,连接,过点D作交的延长线于点E.延长交的延长线于点F,且
(1)求证:是的切线:
(2)设,,求y与x的数量关系式.
第23题图
24.(本题满分12分)
在中,,分别取、的中点并且同时将这两个中点绕点C按顺时针方向旋转依次得到点D、E,记旋转角为(),连接、、,如图所示.
(1)当时,求证:;
(2)若,当B、D、E三点共线时,求线段的长;
(3)当时,延长交于点H,连接,探究线段,,之间的数量关系并说明理由.
(备用图)(备用图)
25.(本题满分12分)
已知二次函数(),顶点为P,且二次函数的图像恒过两定点A、B(点A在点B的左侧).
(1)当时,求该二次函数的顶点坐标;
(2)在(1)的条件下,二次函数的图像上是否存在一点D,使得,若存在,求出点D的横坐标;若不存在,请说明理由;
(3)将点P先沿水平方向平移个单位,再向下移动个单位得到,若二次函数经过点,在二次函数的图像上存在点Q,使得的最小值为4,求m的取值范围.
广东省广州市南沙区2023-2024学年九年级上学期期末数学试题(无答案): 这是一份广东省广州市南沙区2023-2024学年九年级上学期期末数学试题(无答案),共6页。试卷主要包含了考生必须保持答题卡的整洁,考试时不可使用计算器,下列说法正确的是,古印度有这样一首诗等内容,欢迎下载使用。
广东省广州市越秀区2023-2024学年九年级上学期期末数学试题(无答案): 这是一份广东省广州市越秀区2023-2024学年九年级上学期期末数学试题(无答案),共7页。试卷主要包含了 考生必须保证答题卡的整洁等内容,欢迎下载使用。
广东省广州市海珠区2023-2024学年七年级上学期期末考试数学试题: 这是一份广东省广州市海珠区2023-2024学年七年级上学期期末考试数学试题,共2页。












