山东省菏泽市单县2022-2023学年七年级下学期期末数学试题（解析版）

这是一份山东省菏泽市单县2022-2023学年七年级下学期期末数学试题（解析版），共19页。

1．本试题共26道题，满分120分，考试时间120分钟；
2．请把答案写在答题卡上，选择题用2B铅笔填涂，非选择题用0.5mm的黑色签字笔书写在答题卡的指定区域内，写在其它区域不得分．
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个选项是正确的，请把正确选项的序号涂在答题卡相应的位置．）
1. 下列各式计算正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】利用同底数幂的乘除法的法则，幂的乘方与积的乘方的法则以及完全平方公式对各项进行运算即可．
【详解】解：A、，故错误，不合题意；
B、，故错误，不合题意；
C、，故错误，不合题意；
D、，故正确，符合题意；
故选：D．
【点睛】本题主要考查完全平方公式，幂乘方与积的乘方，同底数幂的乘除法，解答的关键是对相应的运算法则的掌握．
2. “白日不到处，青春恰自来．苔花如米小，也学牡丹开．”这是清朝袁牧的一首诗《苔》．若苔花的花粉直径约为m，用科学记数法表示，则n为（ ）
A. B. C. 5D. 6
【答案】B
【解析】
【分析】根据科学记数法的表示方法，将进行表示即可得出结果．
【详解】解：；更多优质滋源请 家 威杏 MXSJ663 ∴n为；
故选B．
【点睛】本题考查科学记数法．熟练掌握科学记数法的表示方法，为整数，是解题的关键．
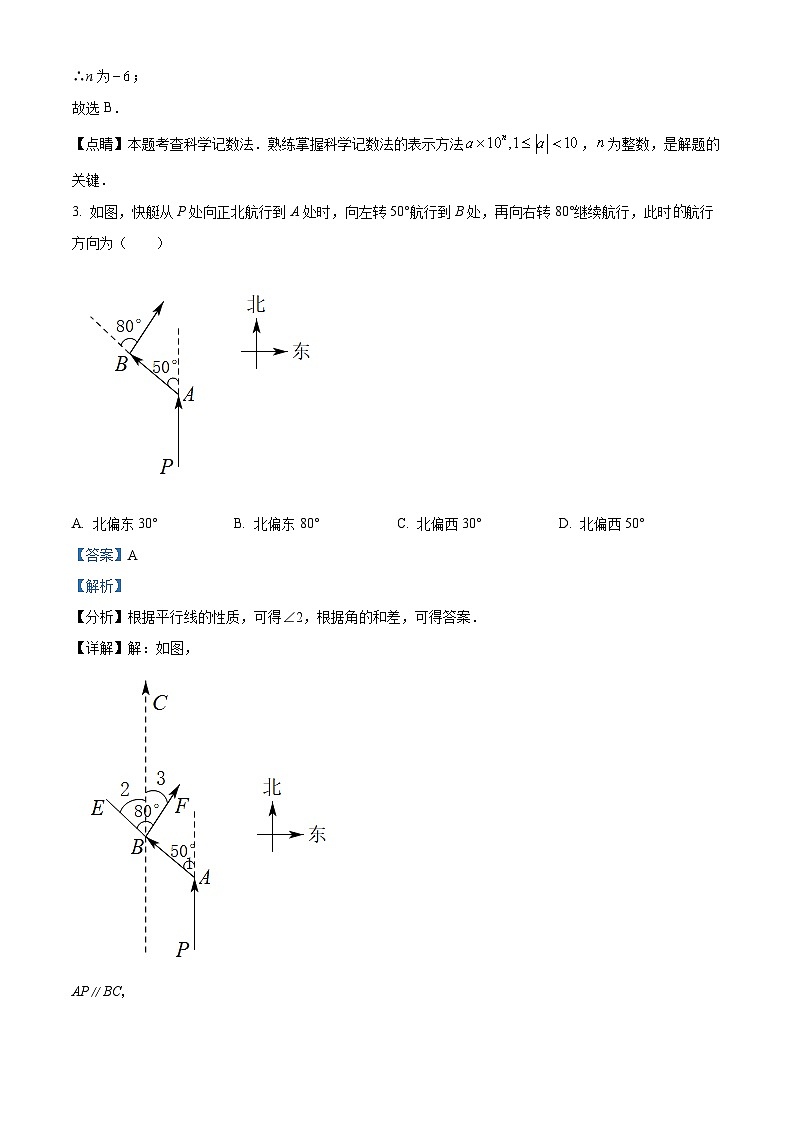
3. 如图，快艇从P处向正北航行到A处时，向左转50°航行到B处，再向右转80°继续航行，此时航行方向为（ ）
A. 北偏东30°B. 北偏东80°C. 北偏西30°D. 北偏西50°
【答案】A
【解析】
【分析】根据平行线的性质，可得∠2，根据角的和差，可得答案．
【详解】解：如图，
AP∥BC，
∴∠2=∠1=50°，
∵∠EBF=80°=∠2+∠3，
∴∠3=∠EBF﹣∠2=80°﹣50°=30°，
∴此时的航行方向为北偏东30°，
故选A．
【点睛】本题考查了方向角，利用平行线的性质得出∠2是解题关键．
4. 如图，已知直线AB∥CD，∠C=115°，∠A=25°，则∠E=
A. 70°B. 80°
C. 90°D. 100°
【答案】C
【解析】
【分析】由AB∥CD可以推出∠EFB=∠C=115°，又因为∠A=25°，所以∠E=∠EFB-∠A，就可以求出∠E．
【详解】∵AB∥CD，
∴∠EFB=∠C=115°，
∵∠A=25°，
∴∠E=∠EFB−∠A=115°−25°=90°.
故选C.
【点睛】考查了平行线的性质以及三角形外角的性质，掌握两直线平行同位角相等是解题的关键.
5. 小明有两根长度为4cm 和10cm的木棒，他想钉一个三角形木框，现桌子上有如下长度的4根木棒，你认为他应该选择 （ ）
A. 3cmB. 5cmC. 8cmD. 15cm
【答案】C
【解析】
【分析】根据三角形三边关系得出第三边的取值范围，判断即可．
【详解】解：∵两根长度为4cm 和10cm的木棒，
则第三边的取值范围为：，
即：，
故选：C．
【点睛】本题考查了三角形的三边关系，熟知三角形三边关系：两边之和大于第三边，两边只差小于第三边，是解本题的关键．
6. 若点M(x，y)满足，则点M所在象限是（ ）
A. 第一象限或第三象限B. 第二象限和第四象限
C. 第一象限或第二象限D. 不能确定
【答案】B
【解析】
【分析】利用完全平方公式展开得到xy=-1，再根据同号得正判断出x、y异号，然后根据各象限内点的坐标特征解答．
【详解】解：∵（x+y）2=x2+2xy+y2，
∴2xy=-2，
∴xy=-1，
∴x、y异号，
∴点M（x，y）在第二象限或第四象限．
故选：B．
【点睛】本题考查了点的坐标，求出x、y异号是解题的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
7. 要使多项式不含的一次项，则与的关系是（ ）
A. 相等B. 互为相反数
C. 互为倒数D. 乘积为
【答案】A
【解析】
【分析】计算乘积得到多项式，因为不含x的一次项，所以一次项的系数等于0，由此得到p-q=0，所以p与q相等.
【详解】解：
∵乘积的多项式不含x的一次项
∴p-q=0
∴p=q
故选择A
【点睛】此题考查整式乘法的运用，注意不含的项即是该项的系数等于0.
8. 已知关于的代数式是一个完全平方式，则的值为（ ）
A. 3B. C. D. 3或
【答案】D
【解析】
【分析】这里首末两项是x和2这两个数的平方，那么中间一项为加上或减去x和2的积的2倍，据此解答，即可．
【详解】解：∵关于的代数式是一个完全平方式，，
∴或，
解得：或3．
故选：D
【点睛】本题主要考查了完全平方公式，熟练掌握是解题的关键．
9. 将一副三角板的直角顶点重合按如图放置，，，小明得到下列结论：
①如果，则；
②；
③如果，则；
④如果，则．
其中正确的结论有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
【分析】根据平行线的性质和判定和三角形内角和定理逐个判断即可．
【详解】解：∵∠2＝30°，∠CAB＝90°，
∴∠1＝60°，
∵∠E＝60°，
∴∠1＝∠E，
∴，故①正确；
∵∠CAB＝∠DAE＝90°，
∴∠BAE+∠CAD＝90°﹣∠1+90°+∠1＝180°，故②正确；
∵，∠B＝45°，
∴∠3＝∠B＝45°，
∵∠2+∠3＝∠DAE＝90°，
∴∠2＝45°，故③错误；
∵∠CAD＝150°，∠BAE+∠CAD＝180°，
∴∠BAE＝30°，
∵∠E＝60°，
∴∠BOE＝∠BAE+∠E＝90°，
∴∠4+∠B＝90°，
∵∠B＝45°，
∴∠4＝45°，
∵∠C＝45°，
∴∠4＝∠C，故④正确；
所以其中正确的结论有①②④共3个，
故选：C．
【点睛】本题考查了三角形的内角和定理和平行线的性质和判定，能灵活运用定理进行推理是解此题的关键．
10. “鸡兔同笼”是我国古代著名的数学趣题之一．大约在1500年前成书的《孙子算经》中，就有关于“鸡兔同笼”的记载：“今有雏兔同笼，上有三十五头，下有九十四足，问兔各几何？”这四句话的意思是：有若干只鸡兔关在一个笼子里，从上面数，有35个头，从下面数，有94条腿，问笼中各有鸡和兔（ ）只
A. 笼中各有12只鸡，23只兔
B. 笼中各有23只鸡，12只兔
C. 笼中各有13只鸡，22只兔
D. 3笼中各有22只鸡，13只兔
【答案】B
【解析】
【分析】设笼中有鸡x只，兔有y只，根据一只鸡有两只脚一个头，一只兔有四只脚一个头，结合题意建立二元一次方程组求解即可．
【详解】解：设笼中有鸡x只，兔有y只，
由题意，，
解得：，
∴笼中各有23只鸡，12只兔，
故选：B．
【点睛】本题考查二元一次方程组的实际应用，理解题意，准确建立方程组并求解是解题关键．
二、填空题（共10小题，每小题3分，共30分，只要求把结果填写在答题卡的相应区域内）
11. 计算：______．
【答案】2
【解析】
【分析】根据零次幂，负整数指数幂，化简绝对值进行计算即可求解．
【详解】解：
故答案为：2．
【点睛】本题考查了实数的混合运算，掌握零次幂，负整数指数幂的运算法则是解题的关键．
12. 若，则___________．
【答案】4
【解析】
【分析】先求出，再根据同底数幂除法的逆运算法则求解即可．
【详解】解：∵，
∴，即，
∴，
故答案为：4．
【点睛】本题主要考查了幂的乘方运算，同底数幂除法的逆运算，熟知相关计算法则是解题的关键．
13. 一个多边形外角和是内角和的，则这个多边形的边数为________．
【答案】11
【解析】
【分析】多边形的内角和定理为，多边形的外角和为360°，根据题意列出方程求出n的值．
【详解】解：根据题意可得：，
解得： ，
故答案为：11．
【点睛】本题主要考查的是多边形的内角和公式以及外角和定理，属于基础题型．记忆理解并应用这两个公式是解题的关键．
14. 下列说法中正确的有______（填所有正确结论的序号）．
（1）直角三角形只有一条高；
（2）边形共有条对角线；
（3）半径相等的两个圆是等圆；
（4）如果一个多边形的各边都相等，那么它是正多边形；
（5）圆是平面内到定点的距离等于定长的点的集合；
【答案】（3）（5）##（5）（3）
【解析】
【分析】根据圆的集合定义，正多边形的定义，多边形的定义等知识一一判断即可．
【详解】解：（1）直角三角形有三条高，故不符合题意；
（2）边形共有条对角线，故不符合题意；
（3）半径相等的两个圆是等圆，故符合题意；
（4）如果一个多边形的各边都相等，各角都相等，那么它是正多边形，故不符合题意；
（5）圆是平面内到定点的距离等于定长的点的集合，故符合题意．
故答案为：（3）（5）．
【点睛】本题考查圆的集合定义，正多边形的定义，多边形的定义等知识，解题的关键是掌握基本知识，属于中考常考题型．
15. 在平面直角坐标系中，若点和点关于轴对称，则______．
【答案】
【解析】
【分析】利用关于轴对称点的性质，纵坐标相等，横坐标互为相反数，进而得出答案．
【详解】解：点和点 关于轴对称，
，
解得，
．
故答案为：．
【点睛】此题主要考查了关于轴对称点的性质，正确掌握关于轴对称点的性质是解题关键．
16. 已知关于，的方程组和的解相同，则的值为______．
【答案】0
【解析】
【分析】联立不含与的方程组成方程组，求出方程组的解得到与的值，进而求出与的值，代入即可求解．
【详解】解：解得，
，
把代入得，
，
解得，
．
故答案为：0．
【点睛】此题考查了二元一次方程组的解，以及解二元一次方程组，方程组的解即为能使方程组中两方程都成立的未知数的值．
17. 如图，， 平分，，，则______________．
【答案】##25度
【解析】
【分析】先根据平行线的性质得到的度数，，再根据角平分线的定义得到的度数，再结合垂直的定义得到的度数，根据平角的定义即可求解．
【详解】解：∵， 平分，，
∴，
∴．
∵，
∴．
∴，
∴．
故答案为：##25度．
【点睛】本题考查了平行线的性质及角平分线的定义，是中学阶段的常规题．
18. 如图，在中，，，，则______度．
【答案】20
【解析】
【分析】根据三角形外角的性质可得出、，结合、及，即可得出，解之即可解答．
【详解】解：，，
．
又，
．
，
，
．
故答案为：20°．
【点睛】本题主要考查了三角形外角的性质，利用三角形外角的性质结合找出是解答本题的关键．
19. 若n满足，则的值是 _____．
【答案】0
【解析】
【分析】利用完全平方公式即可求解．
【详解】接：∵，
∴，
∴，
∴．
故答案为：0．
【点睛】本题考查了完全平方公式，掌握完全平方公式：是解题的关键．
20. 如图，在中，，的平分线交于点，是与平分线的交点，是的两外角平分线的交点，若，则的度数______．
【答案】##10度
【解析】
【分析】利用角平分线的定义，可得出，，结合，可得出的度数，再利用三角形的外角性质，即可求出的度数．
【详解】解：平分，平分，
，，
，
又，
．
，
，
．
，
故答案为：．
【点睛】本题考查了三角形的外角性质以及角平分线的定义，牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键．
三、解答题（本题共60分，把解答过程写在答题卡的相应区域内）
21. 先化简，再求值：，其中，．
【答案】，
【解析】
【分析】先利用完全平方公式、平方差公式及多项式乘多项式的法则计算，再去括号、合并同类项即可化简，继而将、的值代入计算可得．
【详解】解：原式
，
当、时，
原式．
【点睛】本题主要考查整式的混合运算化简求值，解题的关键是熟练掌握整式的混合运算顺序和运算法则．
22. 因式分解：
（1）﹣2a3+12a2﹣18a
（2）9a2（x﹣y）+4b2（y﹣x）
【答案】（1）﹣2a（a﹣3）2
（2）（x﹣y）（3a+2b）（3a﹣2b）
【解析】
【分析】（1）原式提取公因式，再利用完全平方公式分解即可．
（2）原式变形后，提取公因式，再利用平方差公式分解即可．
【小问1详解】
原式＝﹣2a（a2﹣6a+9）
＝﹣2a（a﹣3）2
【小问2详解】
原式＝（x﹣y）（9a2﹣4b2）
＝（x﹣y）（3a+2b）（3a﹣2b）．
【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
23. 已知：如图，，，，，
（1）求证：；
（2）求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】（1）根据平行线的判定与性质即可证得结论；
（2）根据平行线的性质求解即可．
【小问1详解】
证明：∵，，
∴，
∴，
∵，
∴，
∴；
【小问2详解】
解：∵，
∴，，
∵，，
∴，
∴，
∴．
【点睛】本题考查平行线的判定与性质，熟练掌握平行线的判定与性质是解答的关键．
24. 已知：，，．
（1）在坐标系中描出各点，画出；
（2）求的面积；
（3）设点在坐标轴上，且的面积为面积的两倍，请直接写出符合条件的点的坐标．
【答案】（1）见解析；（2）；（3）或或或
【解析】
【分析】（1）根据坐标，画出图形即可；
（2）作CE⊥y轴于E，CF⊥x轴于F．根据S△ABC=S四边形CEOF-S△AEC-S△AOB-S△BCF计算即可；
（3）法两种情形分别求解即可解决问题．
【详解】解：（1）如图所示；
（2）作轴于，轴于．
．
（3）当点在轴上时，的面积，
，
或，
当点在轴上时，的面积，
，
或，
综上所述，满足条件的点坐标为或或或．
【点晴】考查作图-复杂作图，三角形的面积、坐标与图形的性质等知识，解题的关键是学会用分割法求三角形面积，学会用分类讨论的思想解决问题．
25. 杭州亚运会将于2023年9月23日举行，某运动品牌赞助商开发了一款新式运动器材，计划15天生产安装360台，送到指定场馆供运动员使用．由于抽调不出足够的熟练工来完成新式运动器材的安装，工厂决定招聘一些新工人．他们经过培训后上岗，也能独立进行新式运动器材的安装．生产开始后，调研部门发现：2名熟练工和1名新工人每天可安装10台新式运动器材；3名熟练工和2名新工人每天可安装16台新式运动器材．
（1）每名熟练工和新工人每天分别可以安装多少台新式运动器材？
（2）如果工厂抽调（）名熟练工，使得招聘的新工人（至少招聘一人）和抽调的熟练工刚好能完成原计划15天的生产任务，那么工厂有哪几种新工人的招聘方案？
【答案】（1）4台， 2台
（2）4种：或或或
【解析】
【分析】（1）设每名熟练工每天可以安装台新式运动器材，每名新工人每天可以安装台新式运动器材，根据“2名熟练工和1名新工人每天可安装10台新式运动器材；3名熟练工和2名新工人每天可安装16台新式运动器材”，可得出关于，的二元一次方程组，解之即可得出结论；
（2）设招聘名新工人，根据招聘的新工人（至少招聘一人）和抽调的熟练工刚好能完成原计划15天的生产任务，可得出关于，的二元一次方程，结合，均为正整数且，即可得出工厂有4种新工人的招聘方案．
【小问1详解】
解：设每名熟练工每天可以安装台新式运动器材，每名新工人每天可以安装台新式运动器材，
根据题意得：，
解得：．
答：每名熟练工每天可以安装4台新式运动器材，每名新工人每天可以安装2台新式运动器材；
【小问2详解】
设招聘名新工人，
根据题意得：，
．
又，均为正整数，且，
或或或，
工厂有4种新工人的招聘方案．
【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用，找准等量关系，正确列出二元一次方程组（或二元一次方程）是解题的关键．
26. 如图①，AD平分∠BAC，AE⊥BC，∠B=38°，∠C=64°．
（1）求∠DAE的度数；
（2）如图②，若把“AE⊥BC”变成“点F在DA的延长线上，FE⊥BC”，∠B=α，∠C=β（α＜β），请用α、β 的代数式表示∠DFE．
【答案】（1）∠DAE的度数为13°；（2）∠DFE=．
【解析】
【分析】（1）先利用三角形内角和定理求出∠BAC=78°，再由角平分线的定义求出∠BAD=39°，由三角形外角的性质得到∠ADE=∠B+∠BAD=77°，再由垂直的定义得到∠AEB=90°，由此即可求解；
（2）同（1）进行求解即可；
详解】解：（1），，
，
平分，
，
，
，
，
．
（2），，
，
平分，
，
，
，
，
．
【点睛】本题主要考查了三角形内角和定理，三角形外角的性质，角平分线的定义，垂直的定义，解题的关键在于能够熟练掌握相关知识进行求解．