
初中数学北师大版七年级上册1.1 生活中的立体图形练习题
展开1.认识柱体、椎体、球体,并能够熟练的进行立体图形的分类;
2.掌握柱体、椎体、球体的特征;
3.掌握柱体特征及其面的个数、棱的条数、顶点个数之间的关系;
4.掌握立体图形的表面积、体积公式;
5.掌握棱柱的顶点数、棱数、面数的计算方法;
6.掌握立体图形的表面积和体积的计算方法.
知识点01 认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
知识点02 立体图形的分类
(1)按形状分类:球,柱体(圆柱、棱柱),椎体(圆锥、棱锥),台体(圆台、棱台).
(2)按构成分类:旋转体(由平面围成的立体图形),旋转体(绕某一轴旋转一周).
知识点03 点、线、面、体
(1)体与体相交成面,面与面相交成线,线与线相交成点.
(2)从运动的观点来看:点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.
(3)从几何的观点来看:点是组成图形的基本元素,线、面、体都是点的集合.
(4)长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体简称体.
(5)面有平面和曲面之分,如长方体由6个平面组成,球由一个曲面组成.
知识点04 棱柱与棱锥的顶点、面、棱数
知识点05 几何体的表面积与体积
(1)几何体的表面积=侧面积+底面积(上、下底的面积和)
(2)常见的几种几何体的表面积的计算公式:
(3)常见的几种几何体的体积的计算公式:
题型01 几何体的识别
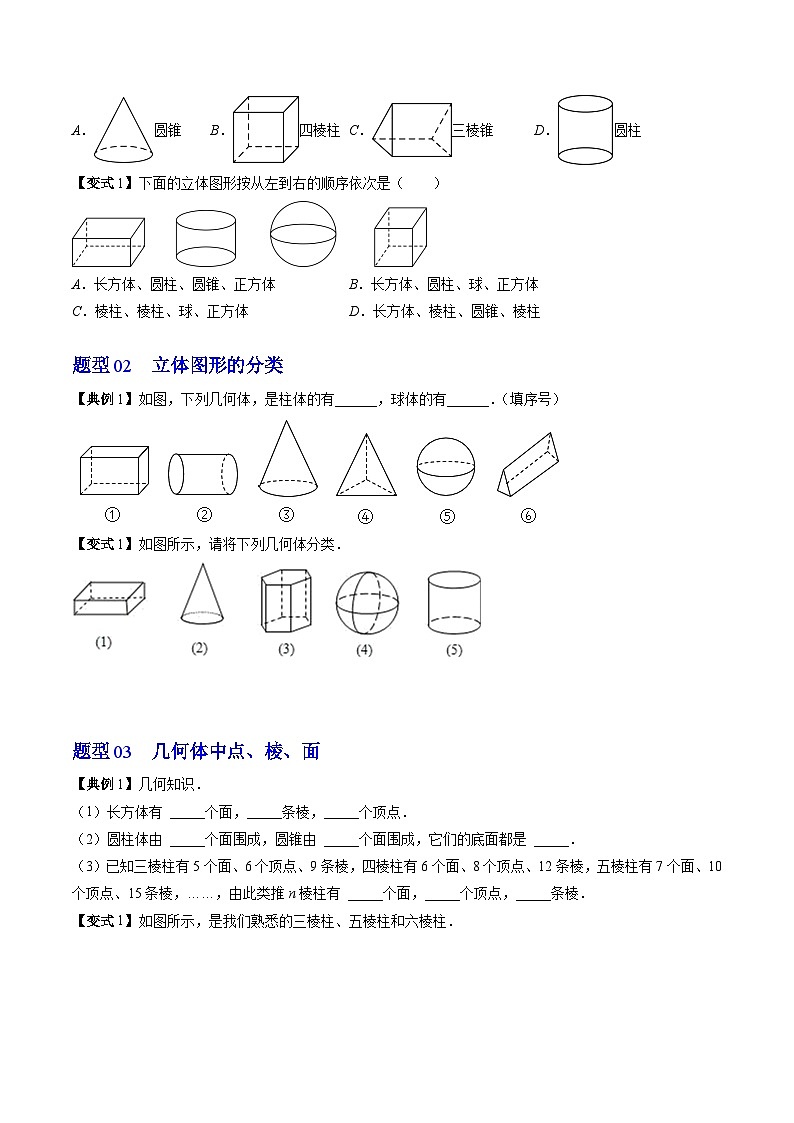
【典例1】下列标注的图形与名称不相符的是( )
A.圆锥B.四棱柱C.三棱锥D.圆柱
【变式1】下面的立体图形按从左到右的顺序依次是( )
A.长方体、圆柱、圆锥、正方体B.长方体、圆柱、球、正方体
C.棱柱、棱柱、球、正方体D.长方体、棱柱、圆锥、棱柱
题型02 立体图形的分类
【典例1】如图,下列几何体,是柱体的有______,球体的有______.(填序号)
【变式1】如图所示,请将下列几何体分类.
题型03 几何体中点、棱、面
【典例1】几何知识.
(1)长方体有 _____个面,_____条棱,_____个顶点.
(2)圆柱体由 _____个面围成,圆锥由 _____个面围成,它们的底面都是 _____.
(3)已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……,由此类推n棱柱有 _____个面,_____个顶点,_____条棱.
【变式1】如图所示,是我们熟悉的三棱柱、五棱柱和六棱柱.
(1)填写下表:
(2)设棱柱(为正整数,且)的顶点数为、棱数为、面数为,根据表中数据猜想________.
题型04 点、线、面、体四者之间的关系
【典例1】当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线B.线动成面C.面动成体D.以上都不对
【变式1】如图,直角三角形绕它的一条直角边所在的直线旋转一周,形成的几何体是__________,这其中蕴含的数学事实是__________.
题型05 平面图形旋转后所得的立体图形
【典例1】图中的圆柱体是由下面哪个图形旋转而成的( )
A.B.C.D.
【变式1】下列各选项中的图形,绕虚线旋转一周,所得的几何体是圆锥的是( )
A. B. C. D.
一、选择题
1.下列图形是平面图形的是( )
A.正方体B.圆C.球D.圆锥
2.下列几何体中,不属于棱柱的是( )
A. B. C. D.
3.中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面B.线动成面,面动成体
C.点动成线,面动成体D.点动成面,面动成线
4.如图,把图形绕着给定的直线旋转一周后形成的几何体是( )
A. B. C. D.
二、填空题
5.五棱柱的面的个数为______.
6.在正方体、长方体、圆柱、圆锥、球、六棱柱、六棱锥中属于柱体有 ___个.
7.笔尖在纸上快速滑动写出了一个又一个字,这说明了_____;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____,“齐天大圣”孙悟空有一个宝贝﹣金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明_____.
8.如图是一个底面各边都相等的六棱柱,它的底面边长为,高为.这个棱柱共有______条棱,______个面,侧面积是______.
三、解答题
9.将如图几何体分类,并说明理由.
10.下列是我们常见的几何体,按要求将其分类(只填写编号).
(1)如果按“柱”“锥球”来分,柱体有______,椎体有______,球有______;
(2)如果按“有无曲面”来分,有曲面的有______,无曲面的有______.
11.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.
12.综合与实践
新年晚会是我们最欢乐的时候,会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.下面是常见的一些多面体:
操作探究:
(1)通过数上面图形中每个多面体的顶点数()、面数()和棱数(),填写下表中空缺的部分:
通过填表发现:顶点数()、面数()和棱数()之间的数量关系是 ,这就是伟大的数学家欧拉(L.Euler,1707—1783)证明的这一个关系式.我们把它称为欧拉公式;
探究应用:
(2)已知一个棱柱只有七个面,则这个棱柱是 棱柱;
(3)已知一个多面体只有8个顶点,并且过每个顶点都有3条棱,求这个多面体的面数.
13.观察下列多面体,并把下表补充完整.
(1)根据表中的规律判断,十二棱柱有___________个面,共有___________个顶点,共有___________条棱;
(2)若某个棱柱由30个面构成,则这个棱柱为___________棱柱;
(3)若一个棱柱的底面多边形的边数为,则它有___________个侧面,共___________个面,共有___________个顶点,共有___________条棱;
(4)观察上表中的结果,请写出,,之间关系式___________.
第01讲 生活中的立体图形
1.认识柱体、椎体、球体,并能够熟练的进行立体图形的分类;
2.掌握柱体、椎体、球体的特征;
3.掌握柱体特征及其面的个数、棱的条数、顶点个数之间的关系;
4.掌握立体图形的表面积、体积公式;
5.掌握棱柱的顶点数、棱数、面数的计算方法;
6.掌握立体图形的表面积和体积的计算方法.
知识点01 认识立体图形
(1)几何图形:从实物中抽象出的各种图形叫几何图形.几何图形分为立体图形和平面图形.
(2)立体图形:有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一个平面内,这就是立体图形.
知识点02 立体图形的分类
(1)按形状分类:球,柱体(圆柱、棱柱),椎体(圆锥、棱锥),台体(圆台、棱台).
(2)按构成分类:旋转体(由平面围成的立体图形),旋转体(绕某一轴旋转一周).
知识点03 点、线、面、体
(1)体与体相交成面,面与面相交成线,线与线相交成点.
(2)从运动的观点来看:点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界.
(3)从几何的观点来看:点是组成图形的基本元素,线、面、体都是点的集合.
(4)长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体,几何体简称体.
(5)面有平面和曲面之分,如长方体由6个平面组成,球由一个曲面组成.
知识点04 棱柱与棱锥的顶点、面、棱数
知识点05 几何体的表面积与体积
(1)几何体的表面积=侧面积+底面积(上、下底的面积和)
(2)常见的几种几何体的表面积的计算公式:
(3)常见的几种几何体的体积的计算公式:
题型01 几何体的识别
【典例1】下列标注的图形与名称不相符的是( )
A.圆锥B.四棱柱C.三棱锥D.圆柱
【答案】C
【分析】根据每一个几何体的特征逐一判断即可.
【详解】解:A.是圆锥,故A不符合题意;
B.是四棱柱,故B不符合题意;
C.是三棱柱,不是三棱锥,故C符合题意;
D.是圆柱,故D不符合题意;
故选:C.
【点睛】本题考查了认识立体图形,熟练掌握每一个几何体的特征是解题的关键.
【变式1】下面的立体图形按从左到右的顺序依次是( )
A.长方体、圆柱、圆锥、正方体B.长方体、圆柱、球、正方体
C.棱柱、棱柱、球、正方体D.长方体、棱柱、圆锥、棱柱
【答案】B
【分析】观察立体图形,进行作答即可.
【详解】解:下面的立体图形按从左到右的顺序依次是:长方体、圆柱、球、正方体;
故选B.
【点睛】本题考查常见的立体图形.熟练掌握常见的立体图形,是解题的关键.
题型02 立体图形的分类
【典例1】如图,下列几何体,是柱体的有______,球体的有______.(填序号)
【答案】 ①②⑥ ⑤
【分析】根据立体图形的特征即可得到答案.
【详解】解:柱体的有①②⑥;球体有⑤.
故答案为:①②⑥,⑤
【点睛】本题考查了认识立体图形,熟知立体图形的特征并知道他们的名称是解题关键.
【变式1】如图所示,请将下列几何体分类.
【答案】答案不唯一,见解析
【分析】对于立体图形的分类,可按照不同标准进行,①按照立体图形的种类分类;②根据立体图形包含的平面类型分类.
【详解】解:方法一:(1)、(3)、(5)是一类,都是柱体;(2)是锥体;(4)是球体.
方法二:(1)、(3)是一类,全是由平面构成的;(2)、(5)是一类,既有平面,又有曲面;(4)是一类,只有曲面.
【点睛】本题考查立体图形的认识,掌握分类时的标准选择是解题关键.
题型03 几何体中点、棱、面
【典例1】几何知识.
(1)长方体有 _____个面,_____条棱,_____个顶点.
(2)圆柱体由 _____个面围成,圆锥由 _____个面围成,它们的底面都是 _____.
(3)已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……,由此类推n棱柱有 _____个面,_____个顶点,_____条棱.
【答案】 6 12 8 3 2 圆形
【分析】(1)根据长方体的特征即可得到答案;
(2)根据圆柱和圆锥的特征即可得到答案;
(3)根据棱柱的特征进行分析,即可得到答案.
【详解】解:(1)长方体有6个面,12条棱,8个顶点,
故答案为:6,12,8;
(2)圆柱体由3个面围成,圆锥由2个面围成,它们的底面都是圆形,
故答案为:3,2,圆形;
(3)已知三棱柱有5个面、6个顶点、9条棱,四棱柱有6个面、8个顶点、12条棱,五棱柱有7个面、10个顶点、15条棱,……,由此类推n棱柱有个面,个顶点,条棱,
故答案为:,,.
【点睛】本题考查了常见几何体的基础知识,解题关键是具备空间想象能力.
【变式1】如图所示,是我们熟悉的三棱柱、五棱柱和六棱柱.
(1)填写下表:
(2)设棱柱(为正整数,且)的顶点数为、棱数为、面数为,根据表中数据猜想________.
【答案】(1),,;,,;,,
(2)
【分析】(1)根据所给的图形,数一数直接得出结果;
(2)把(1)中的结果代入,即可发现规律.
【详解】(1)根据图形,可以得出三棱柱有个顶点,个面,条棱;五棱柱有个顶点,个面,条棱;六棱柱有个顶点,个面,条棱;
故答案为:,,;,,;,,.
(2)三棱柱:,,,
;
五棱柱:,,,
;
六棱柱: ,,,
;
猜想:.
【点睛】本题主要考查了几何体的结构特征,根据所给的材料,仔细观察图形,找出一般规律是解本题的关键.
题型04 点、线、面、体四者之间的关系
【典例1】当你用笔在纸上写字时,你的笔尖实现了( )
A.点动成线B.线动成面C.面动成体D.以上都不对
【答案】A
【分析】笔尖点在纸上是一个点,写字滑动笔尖就是一条直线,即点动成线.
【详解】解:当你用笔在纸上写字时,你的笔尖实现了点动成线,
故选:A.
【点睛】本题考查了点动成线,理解点动成线是解题关键.
【变式1】如图,直角三角形绕它的一条直角边所在的直线旋转一周,形成的几何体是__________,这其中蕴含的数学事实是__________.
【答案】 圆锥 面动成体
【分析】根据直角三角形绕它的一条直角边所在的直线旋转一周,形成的几何体是圆锥,以及面、体之间的关系进行作答即可.
【详解】解:由题意知,直角三角形绕它的一条直角边所在的直线旋转一周,形成的几何体是圆锥,这其中蕴含的数学事实是面动成体,
故答案为:圆锥,面动成体.
【点睛】本题考查了平面图形旋转后所得的立体图形,面、体之间的关系.解题的关键在于对知识的熟练掌握.
题型05 平面图形旋转后所得的立体图形
【典例1】图中的圆柱体是由下面哪个图形旋转而成的( )
A.B.C.D.
【答案】B
【分析】根据圆柱可以看成绕矩形的一边旋转得到,由此判断即可.
【详解】解:圆柱可以看成绕矩形的一边旋转得到,观察图象可知,圆柱的高大于底面圆的直径,
故选项B符合题意,
故选:B.
【点睛】本题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体.
【变式1】下列各选项中的图形,绕虚线旋转一周,所得的几何体是圆锥的是( )
A. B. C. D.
【答案】B
【分析】根据面动成体的知识逐项判断即可得.
【详解】A、本选项中的图形绕虚线旋转一周,所得的几何体是球,不符合题意;
B、本选项中的图形绕虚线旋转一周,所得的几何体是圆锥,符合题意;
C、本选项中的图形绕虚线旋转一周,所得的几何体是圆柱,不符合题意;
D、本选项中的图形绕虚线旋转一周,所得的几何体是圆台,不符合题意;
故选:B.
【点睛】本题考查了面动成体以及基本几何体的认识,正确掌握常见几何体的特点是解题的关键.
一、选择题
1.下列图形是平面图形的是( )
A.正方体B.圆C.球D.圆锥
【答案】B
【分析】根据题意可知,正方体、球、圆锥体都是立体图形,圆是平面图形,据此即可求解.
【详解】解:圆是平面图形,正方体、球、圆锥体都是立体图形,故B正确.
故选:B.
【点睛】本题主要考查了平面图形与立体图形的认识,正确的区分是解题的关键.
2.下列几何体中,不属于棱柱的是( )
A. B. C. D.
【答案】B
【分析】有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,由此可选出答案.
【详解】解:A. 该几何体是四棱柱,故不符合题意;
B. 该几何体是四棱锥,故符合题意;
C. 该几何体是三棱柱,故不符合题意;
D.该几何体是六棱柱,故不符合题意.
故选:B.
【点睛】本题考查了立体图形的识别,注意几何体的分类,一般分为柱体、锥体和球,柱体又分为圆柱和棱柱,椎体又分为圆锥和棱锥.
3.中华武术是中国传统文化之一,是中华民族在日常生活中结合社会哲学、中医学、伦理学、兵学、美学、气功等多种传统文化思想和文化观念,注重内外兼修,诸如整体观、阴阳变化观、形神论、气论、动静说、刚柔说等,逐步形成了独具民族风貌的武术文化体系.“枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面B.线动成面,面动成体
C.点动成线,面动成体D.点动成面,面动成线
【答案】A
【分析】枪挑是用枪尖挑,枪尖可看作点,棍可看作线,转化成数学思想即可.
【详解】所以由题意可得:从数学的角度可解释为点动成线,线动成面.
故选:A.
【点睛】本题考查了点、线、面、体的知识点,熟练掌握点、线、面之间的关系是解题的关键.
4.如图,把图形绕着给定的直线旋转一周后形成的几何体是( )
A. B. C. D.
【答案】D
【分析】根据几何体的特征判断即可.
【详解】解:观察如图,把图形绕着给定的直线旋转一周后形成的几何体可能是:空心的圆柱体,
故选:D.
【点睛】本题考查了点、线、面、体,熟练掌握每一个几何体的特征是解题的关键.
二、填空题
5.五棱柱的面的个数为______.
【答案】7
【分析】五棱柱共有2个底面,5个侧面,据此可以解答.
【详解】解:五棱柱共有2个底面,5个侧面,共7个面,
故答案为7.
【点睛】本题考查了认识立体图形的知识,解题的关键是了解n棱柱有两个底面加上n个侧面,共有个面.
6.在正方体、长方体、圆柱、圆锥、球、六棱柱、六棱锥中属于柱体有 ___个.
【答案】4
【分析】根据柱体、锥体、球体的概念进行判断即可.
【详解】解:属于柱体的有:正方体、长方体、圆柱,六棱柱,共4个,圆锥、六棱锥属于锥体,球属于球体,
故答案为:4.
【点睛】本题考查认识立体图形,掌握锥体、柱体、球体的特征是正确判断的关键.
7.笔尖在纸上快速滑动写出了一个又一个字,这说明了_____;直角三角形绕它的直角边旋转一周,形成了一圆锥体,这说明了_____,“齐天大圣”孙悟空有一个宝贝﹣金箍棒,当他快速旋转金箍棒时,展现在我们眼前的是一个圆的形象,这说明_____.
【答案】 点动成线 面动成体 线动成面
【分析】根据“点动成线,线动成面,面动成体”进行分析即可.
【详解】解:“笔尖”可近似看作“点”笔尖在纸上快速滑动,说明点动成线,直角三角形可以看作是“面”,旋转一周形成了一圆锥体,说明“面动成体”,“金箍棒”可近似看作“线段”,快速旋转金箍棒,展现在我们眼前的是一个圆的形象,实际上就是“线动成面”,
故答案为:点动成线,面动成体,线动成面.
【点睛】本题考查了点、线、面、体,理解“点动成线,线动成面,面动成体”是解题关键.
8.如图是一个底面各边都相等的六棱柱,它的底面边长为,高为.这个棱柱共有______条棱,______个面,侧面积是______.
【答案】
【分析】根据图形,分侧面上的棱与底面上的棱计算即可得棱的数目,棱柱的面分侧面与底面两种,根据侧面是长方形,然后根据长方形的面积公式计算即可求得侧面积.
【详解】解:这个棱柱共有棱:条;
有6个侧面,2个底面,共有个面,
它的侧面积为:.
故答案为:,,.
【点睛】本题考查了认识立体图形,几何体的侧面积,掌握基本立体图形的性质是解题的关键.
三、解答题
9.将如图几何体分类,并说明理由.
【答案】柱体:①正方体,②长方体,③圆柱体,⑥四棱柱,⑦三棱柱;锥体:④圆锥;球体:⑤球;见解析
【分析】根据立体图形的分类:柱体,锥体,球体,可得答案.
【详解】解:根据几何体的概念可得,柱体:①正方体,②长方体,③圆柱体,⑥四棱柱,⑦三棱柱;
锥体:④圆锥;
球体:⑤球.
【点睛】本题考查了认识立体图形,立体图形分为三大类:柱体,锥体,球体.
10.下列是我们常见的几何体,按要求将其分类(只填写编号).
(1)如果按“柱”“锥球”来分,柱体有______,椎体有______,球有______;
(2)如果按“有无曲面”来分,有曲面的有______,无曲面的有______.
【答案】(1)①②⑥;③④;⑤
(2)②③⑤;①④⑥
【分析】(1)根据立体图形的特点从柱体的形状特征考虑.
(2)根据面的形状特征考虑.
【详解】(1)解:∵(1)是四棱柱,(2)是圆柱,(3)是圆锥,(4)是棱锥,(5)是球,(6)是三棱柱,
∴柱体有(1),(2),(6),锥体有(3),(4),球有(5),
故答案为:(1),(2),(6);(3),(4);(5);
(2)∵(2)(3)(5)有曲面,其它几何体无曲面,
∴按“有无曲面”来分,有曲面的有(2),(3),(5),无曲面的有:(1),(4),(6),
故答案为:(2),(3),(5);(1),(4),(6).
【点睛】本题考查了认识立体图形,解决本题的关键是认识柱体的形状特征.
11.如图1至图3是将正方体截去一部分后得到的多面体.
(1)根据要求填写表格:
(2)猜想f、v、e三个数量间有何关系;
(3)根据猜想计算,若一个多面体有顶点数2013个,棱数4023条,试求出它的面数.
【答案】(1)7,9,14.6,8,12,7,10,15;
(2);
(3)它的面数是2012
【分析】(1)根据图形数出即可;
(2)根据(1)中结果得出;
(3)代入求出即可;
【详解】(1)图1,面数,顶点数,棱数,
图2,面数,顶点数,棱数,
图3,面数,顶点数,棱数,
故答案为:7,9,14.6,8,12,7,10,15.
(2)由表格数据可得:.
(3)∵
∴,
,
即它的面数是2012.
【点睛】本题考查了截一个几何体,图形的变化类的应用,关键是能根据(1)中的结果得出规律
12.综合与实践
新年晚会是我们最欢乐的时候,会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形.下面是常见的一些多面体:
操作探究:
(1)通过数上面图形中每个多面体的顶点数()、面数()和棱数(),填写下表中空缺的部分:
通过填表发现:顶点数()、面数()和棱数()之间的数量关系是 ,这就是伟大的数学家欧拉(L.Euler,1707—1783)证明的这一个关系式.我们把它称为欧拉公式;
探究应用:
(2)已知一个棱柱只有七个面,则这个棱柱是 棱柱;
(3)已知一个多面体只有8个顶点,并且过每个顶点都有3条棱,求这个多面体的面数.
【答案】(1)表见解析,
(2)五
(3)6
【分析】(1)通过观察,发现棱数顶点数面数;
(2)根据棱柱的定义进行解答即可;
(3)由(1)得出的规律进行解答即可.
【详解】(1)解:填表如下:
顶点数()、面数()和棱数()之间的数量关系是,
故答案为:;
(2)解:一个棱柱只有七个面,必有2个底面,
有个侧面,
这个棱柱是五棱柱,
故答案为:五;
(3)解:由题意得:棱的总条数为(条),
由可得,
解得:,
故该多面体的面数为6.
【点睛】本题考查了多面体与棱柱的认识,点线面体的相关概念,正确看出图形中各量之间的关系是解题的关键.
13.观察下列多面体,并把下表补充完整.
(1)根据表中的规律判断,十二棱柱有___________个面,共有___________个顶点,共有___________条棱;
(2)若某个棱柱由30个面构成,则这个棱柱为___________棱柱;
(3)若一个棱柱的底面多边形的边数为,则它有___________个侧面,共___________个面,共有___________个顶点,共有___________条棱;
(4)观察上表中的结果,请写出,,之间关系式___________.
【答案】填表见解析;(1);(2);(3);(4)
【分析】由三棱柱的顶点数为:,棱数为:,面数为:;四棱柱的顶点数为:,棱数为:,面数为:;五棱柱的顶点数为:,棱数为:,面数为:;六棱柱的顶点数为:,棱数为:,面数为:,即可填表.
根据已知的面、顶点和棱与几棱柱的关系,可知棱柱一定有个面,个顶点和条棱,进而得出(1)(2)和(3)的答案;
(4)根据表格可总结出规律得出之间的关系.
【详解】解:填表如下:
(1)十二棱柱有个面,共有个顶点,共有条棱.
故答案为:14,24,36;
(2)某个棱柱由个面构成,则这个棱柱为棱柱.
故答案为:28;
(3)若一个棱柱的底面多边形的边数为,则它有个侧面,共有个面,共有个顶点,共有条棱.
故答案为:,,,;
(4)之间的关系:.
故答案为:.
【点睛】此题主要考查了几何规律型问题,熟记常见棱柱的特征,进而可以总结一般规律:棱柱有个面,个顶点和条棱是解题关键.立体图形
各项个数
n棱柱
顶点个数_2n_,棱个数_3n_,面个数_n+2_,侧棱个数_n_,侧面个数_n_
n棱锥
顶点个数_n+1_,棱个数_2n_,面个数_n+1_,侧棱个数_n_,侧面个数_n_
立体图形
表面积公式
圆柱体
_2πR2+2πRh_(R为圆柱体上下底圆半径,h为圆柱体高)
圆锥体
πr2+nπ(h2+r2)/360(r为圆锥体低圆半径,h为其高,n为圆锥侧面展开图中扇形的圆心角)
长方体
_2(ab+ah+bh)_(a为长方体的长,b为长方体的宽,h为长方体的高)
正方体
_6a2 __(a为正方体棱长)
立体图形
体积公式
圆柱体
__πR2h_(R为圆柱体上下底圆半径,h为圆柱体高)
圆锥体
_1/3πR2h_(R为圆柱体上下底圆半径,h为圆锥体高)
长方体
_abh_(a为长方体的长,b为长方体的宽,h为长方体的高)
正方体
__a3_(a为正方体棱长)
立体图形
顶点数
面数
棱数
三棱柱
五棱柱
六棱柱
面数(f)
顶点数(v)
棱数(e)
图1
图2
图3
多面体
顶点数()
面数()
棱数()
四面体
4
六面体
8
6
八面体
8
12
十二面体
20
30
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数
6
棱数
9
面数
5
立体图形
各项个数
n棱柱
顶点个数_2n_,棱个数_3n_,面个数_n+2_,侧棱个数_n_,侧面个数_n_
n棱锥
顶点个数_n+1_,棱个数_2n_,面个数_n+1_,侧棱个数_n_,侧面个数_n_
立体图形
表面积公式
圆柱体
_2πR2+2πRh_(R为圆柱体上下底圆半径,h为圆柱体高)
圆锥体
πr2+nπ(h2+r2)/360(r为圆锥体低圆半径,h为其高,n为圆锥侧面展开图中扇形的圆心角)
长方体
_2(ab+ah+bh)_(a为长方体的长,b为长方体的宽,h为长方体的高)
正方体
_6a2 __(a为正方体棱长)
立体图形
体积公式
圆柱体
__πR2h_(R为圆柱体上下底圆半径,h为圆柱体高)
圆锥体
_1/3πR2h_(R为圆柱体上下底圆半径,h为圆锥体高)
长方体
_abh_(a为长方体的长,b为长方体的宽,h为长方体的高)
正方体
__a3_(a为正方体棱长)
立体图形
顶点数
面数
棱数
三棱柱
五棱柱
六棱柱
面数(f)
顶点数(v)
棱数(e)
图1
图2
图3
多面体
顶点数()
面数()
棱数()
四面体
4
六面体
8
6
八面体
8
12
十二面体
20
30
多面体
顶点数()
面数()
棱数()
四面体
4
4
6
六面体
8
6
12
八面体
6
8
12
十二面体
20
12
30
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数
6
棱数
9
面数
5
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数
棱数
面数
初中数学北师大版七年级上册第二章 有理数及其运算2.2 数轴同步测试题: 这是一份初中数学北师大版七年级上册第二章 有理数及其运算2.2 数轴同步测试题,共24页。
初中数学北师大版七年级上册2.1 有理数一课一练: 这是一份初中数学北师大版七年级上册2.1 有理数一课一练,共29页。试卷主要包含了掌握正数和负数的数学含义;,掌握有理数的概念及分类;,能够正确的判断有理数的分类,5,3四个数中,是负数的是,51元记作元,那么支出5333,2,,;,5等内容,欢迎下载使用。
北师大版七年级上册2.1 有理数当堂达标检测题: 这是一份北师大版七年级上册2.1 有理数当堂达标检测题,共24页。













