吉林省延边朝鲜族自治州2023-2024学年九年级上学期期末数学试题(无答案)

这是一份吉林省延边朝鲜族自治州2023-2024学年九年级上学期期末数学试题(无答案)，共6页。试卷主要包含了抛物线的顶点坐标是，一元二次方程的根的情况是等内容，欢迎下载使用。

数学试题共6页，包括六道大题，共26道小题。全卷满分120分，考试时间为120分钟。考试结束后，将本试题和答题卡一并交回。
注意事项：
1.答题前，考生务必将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内。
2.答题时，考生务必按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题卷上答题无效。
一、单项选择题（每小题2分，共12分）
1.第19届亚运会于2023年9月在浙江省杭州市举办，下列与杭州亚运会有关的图案中，其中是中心对称图形的是（ ）
A. B.
C. D.
2.下列事件中，属于必然事件的是（ ）
A.抛掷硬币时，正面朝上B.太阳从东方升起
C.经过红绿灯路口，遇到红灯D.负数大于正数
3.抛物线的顶点坐标是（ ）
A.B.C.D.
4.一元二次方程的根的情况是（ ）
A.有两个相等的实数根B.没有实数根
C.有两个不相等的实数根D.无法确定
5.在同一平面内，已知的半径为5，点A在外，则的长度可以等于（ ）
A.6B.5C.3D.0
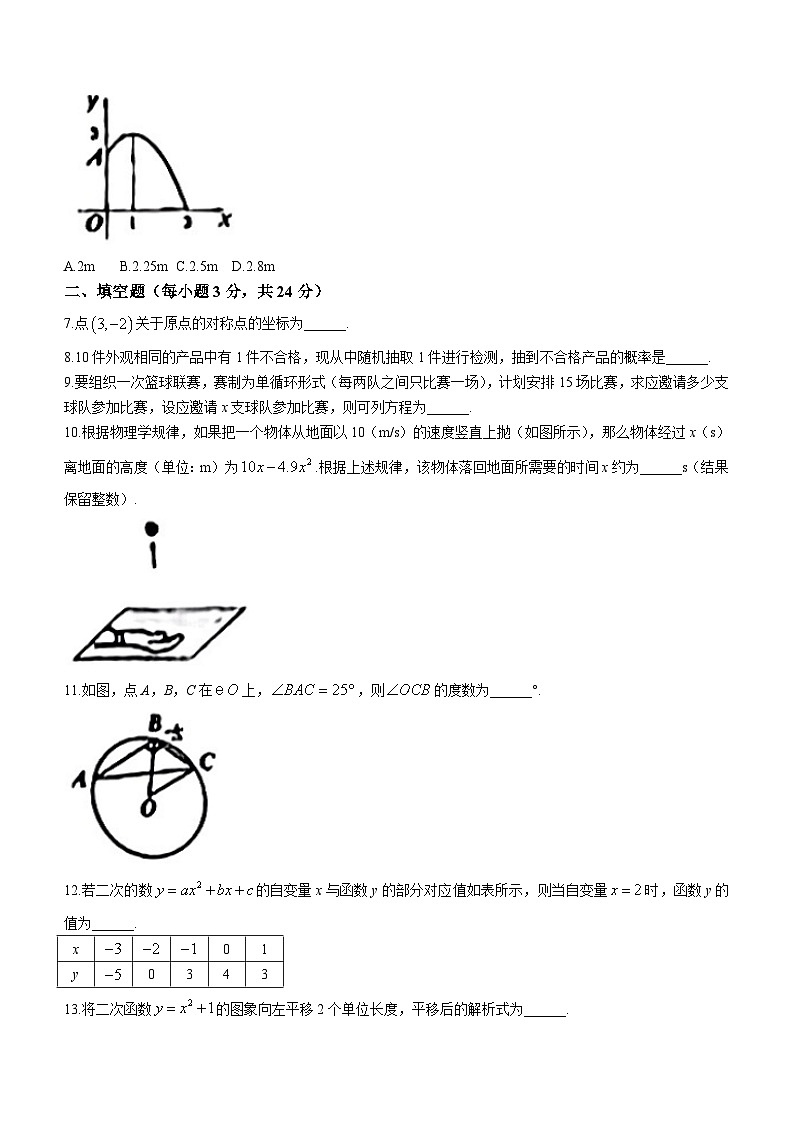
6.如图，要修建一个图形喷水池，在池中心O点竖直安装一根水管，在水管的顶端A处安一个喷水头，使喷出的抛物线形水柱在与池中心O点的水平距离为1m处达到最高，最高高度为3m，水柱落地处离池中心O点距离为3m，则水管的高是（ ）
A.2m
二、填空题（每小题3分，共24分）
7.点关于原点的对称点的坐标为______.
8.10件外观相同的产品中有1件不合格，现从中随机抽取1件进行检测，抽到不合格产品的概率是______.
9.要组织一次篮球联赛，赛制为单循环形式（每两队之间只比赛一场），计划安排15场比赛，求应邀请多少支球队参加比赛，设应邀请x支球队参加比赛，则可列方程为______.
10.根据物理学规律，如果把一个物体从地面以10（m/s）的速度竖直上抛（如图所示），那么物体经过x（s）离地面的高度（单位：m）为.根据上述规律，该物体落回地面所需要的时间x约为______s（结果保留整数）.
11.如图，点A，B，C在上，，则的度数为______°.
12.若二次的数的自变量x与函数y的部分对应值如表所示，则当自变量时，函数y的值为______.
13.将二次函数的图象向左平移2个单位长度，平移后的解析式为______.
14.如图，四边形中，，，，垂足是E，若线段，则______.
三、解答题（每小题5分，共20分）
15.解方程：.
16.两年前生产1吨甲种药品的成本是6400元.随着生产技术的进步，现在生产1吨甲种药品的成本是3600元.求甲种药品成本的年平均下降率。
17.如图，在中，，，求证：.
18.布袋中有红、黄、蓝三种只有颜色不同的球各一个，从中先摸出一个球，记录下它的颜色，将它放回布袋并搅匀，再摸出一个球，记录下颜色.用列表或画树状图的方法求摸出的两个球颜色为“一红一黄”的概率.
四、解答题（每小题7分，共28分）
19.如图，方格纸中的每个小方格都是边长为1个单位长度的正方形.每个小正方形的顶点叫格点，的顶点均在格点上，点O，点M也在格点上.
（1）画出关于直线对称的.
（2）画出绕点O按顺时针方向旋转90°后所得的.
（3）与组成的图形是轴对称图形吗？如果是，请画出所有的对称轴.
20.石拱桥是我国古代人民勤劳和智慧的结晶（如图①），赵州桥是我国古代石拱桥的代表，图②是根据该石拱桥画出的几何图形，桥的主桥拱是圆弧形，表示为，桥的跨度（弧所对的弦长），设所在圆的圆心为O，，为半径，半径，垂足为D.拱高（弧的中点到弦的距离）.
（1）直接写出与的数量关系
（2）求这座石拱桥主桥拱的半径.
21.某水果公司新进了10000千克柑橘，销售人员首先从所有的柑橘中随机地抽取若干柑橘，进行了“柑橘损坏率”统计，并把获得的数据记录在下表中：
（1）写出______ ______ ______精确到0.001）.
（2）估计这批柑橘的损坏概率为______（精确到0.1）.
（3）该水果公司以2元千克的成本进的这批柑橘，公司希望这批柑橘能够获得利润5000元，那么在出售柑橘（已去掉损坏的柑橘）时，求出每千克大约定价为多少元时比较合适（精确到0.1）.
22.如图，将含30°角的直角三角板放入半圆O中，，A，B，C三点恰好在半圆O上，延长到点E，作直线，使得·
（1）求证：是半圆O的切线.
（2）若，求阴影部分的面积.
五、解答题（每小题8分，共16分）
23.某宾馆有50个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满.当每个房间每天的定价每增加10元时，就会有一个房间空闲.如果宾馆对游客居住的每个房间每天需支出20元的各种费用.
（1）若每个房间的定价为每天200元，求宾馆的利润.
（2）求每个房间的定价为每天多少元时，宾馆利润最大.
24.如图，已知，点P为射线上任意一点（点P与点B不重合），分别以、为边在的内部作等边和，连接并延长交于点F.
（1）如图①，若，点A，E，P恰好在一条直线上时，则直接写出______.
（2）如图②，当点P为射线上任意一点时，求证：.
（3）如图②，，，则直接写出______.
六、解答题（每小题10分，共20分）
25.如图，是等腰直角三角形，其中，.动点P从点A出发以1cm/s的速度向终点B运动（动点P不与点A、B重合），过点P作，交折线于点Q，将线段绕点Q逆时针方向旋转90°得到线段，连接.设与重合部分图形的面积为S（），动点P运动的时间为t（s）.
（1）当点M落在边上时，求t的值.
（2）求出S关于t的函数解析式，并写出自变量t的取值范围.
（3）在动点P的整个运动过程中，直接写出S的最大值.
26.如图，抛物线经过、两点，点D在该抛物线上运动，设点D的横坐标为.
（1）求该抛物线的解析式.
（2）当时，过点D作轴，交直线于E点，求线段的最大值.
（3）当时，若抛物线在点D，点B之间部分（包括点D，点B两个端点）的最高点和最低点的纵坐标的差为3时，求m的值.
（4）设抛物线与线段围成的封闭图形记作图形P，点C为直线上的一个动点（点C不与点A重合），设点C的横坐标为n，以为边向下作正方形，当M、N两点中只有一个点在图形P的内部时（不包括边界），直按写出n的取值范围.x
0
1
y
0
3
4
3
柑橘总质量（n/千克）
损坏柑橘质量（m/千克）
柑橘损坏的频率（）
50
5.50
0.110
100
10.50
0.105
150
15.15
0.101
200
19.42
0.097
250
24.35
0.097
300
30.93
a
350
35.32
0.101
400
39.24
b
450
44.57
0.099
500
51.54
c