吉林省松原市前郭尔罗斯蒙古族自治县洪泉乡中学2020-2021学年九年级一轮复习模拟试卷 数学试卷（五）（含答案）

这是一份吉林省松原市前郭尔罗斯蒙古族自治县洪泉乡中学2020-2021学年九年级一轮复习模拟试卷 数学试卷（五）（含答案），共18页。
数学试卷（五）
【满分：150分】
一、选择题（本大题有12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.2019的倒数的相反数是( )
A.B.C.D.2019
2.如图，长方形绕它的一条边所在的直线旋转一周形成的几何体是( )

A. B. C. D.
3.若,则的值为( )
A.2B.3C.4D.5
4.如图，是的直径，切于点交于点C，连接.若，则等于( )

A.B.C.D.
5.若，则的值是( )
A.4B.3C.2D.1
6.如图是与位似的三角形的几种画法，其中正确的有( )

A.1个B. 2个C.3个D. 4个
7.某经销商销售一批电话手表，第一个月以550元/块的价格售出60块，第二个月起降价，以500元/块的价格将这批电话手表全部售出，销售总额超过了5.5万元.这批电话手表至少有( )
A.103块B.104块C.105块D.106块
8.在公园内，牡丹按正方形种植，在它的周围种植芍药，如图反映了牡丹的列数(n)和芍药的数量规律，那么当时，芍药的数量为( )

A.84株 B.88株 C.92株 D.121株
9.如图，小明想要测量学校操场上旗杆的高度，他作了如下操作：（1）在点C处放置测角仪，测得旗杆顶的仰角；（2）量得测角仪的高度；（3）量得测角仪到旗杆的水平距离，利用锐角三角函数解直角三角形的知识，旗杆的高度可表示为( )

A.B.C.D.
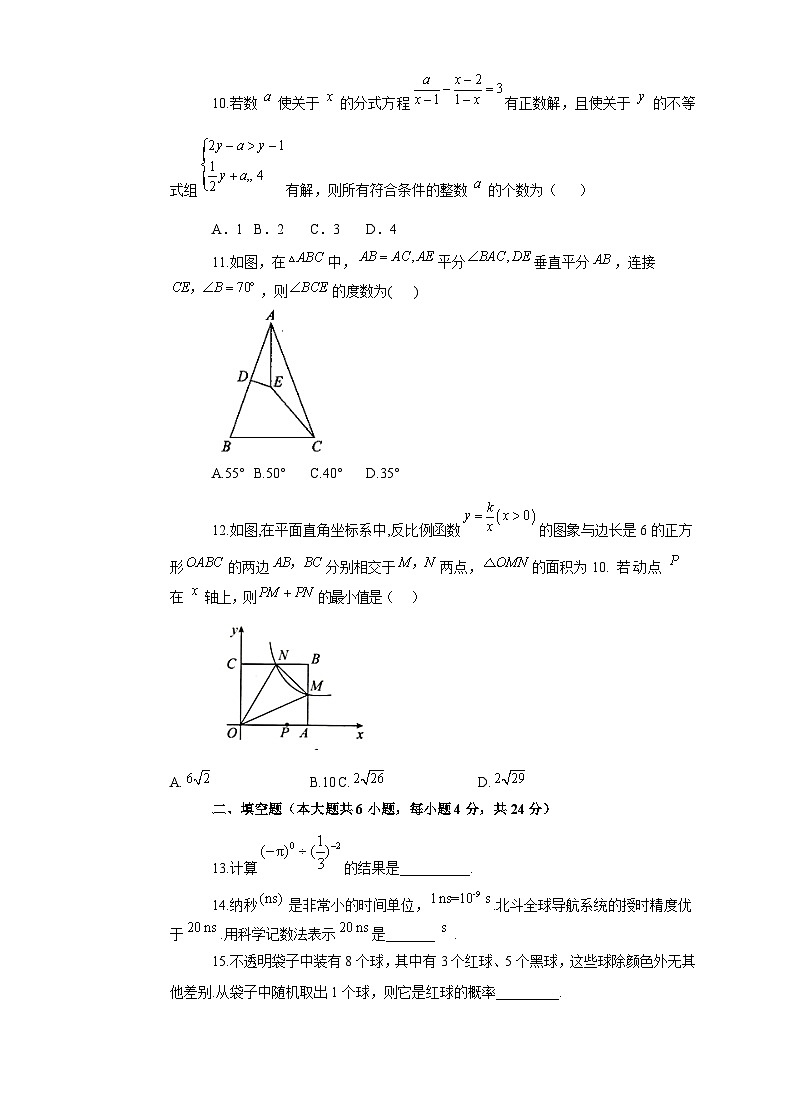
10.若数使关于的分式方程有正数解，且使关于的不等式组有解，则所有符合条件的整数的个数为（ ）
A．1B．2C．3D．4
11.如图，在中，平分垂直平分，连接，则的度数为( )

A.55°B.50°C.40°D.35°
12.如图,在平面直角坐标系中,反比例函数的图象与边长是6的正方形的两边分别相交于两点，的面积为10. 若动点在轴上，则的最小值是（ ）
A. B.10C. D.
二、填空题（本大题共6小题，每小题4分，共24分）
13.计算的结果是__________.
14.纳秒是非常小的时间单位，.北斗全球导航系统的授时精度优于.用科学记数法表示是_______.
15.不透明袋子中装有8个球，其中有3个红球、5个黑球，这些球除颜色外无其他差别.从袋子中随机取出1个球，则它是红球的概率_________.
16.如图，在中，，,，将绕点A逆时针旋转30°后得到， 点B经过的路径为弧，则图中阴影部分的面积为_____________.

17.甲、乙两车分别从两地同时出发，相向行驶，已知甲车的速度大于乙车的速度，甲车到达B地后马上以另一速度原路返回A地（掉头的时间忽略不计），乙车到达A地以后即停在A地等待甲车．如图所示为甲乙两车间的距离y（千米）与甲车的行驶时间x（小时）之间的函数图象，则当乙车到达A地的时候，甲车与A地的距离为 千米

18.某班级从文化用品市场购买了签字笔和圆珠笔共15支，所付金额大于26元，但小于27元.已知签字笔每支2元，圆珠笔每支1.5元，则签字笔购买了_________支.
三、解答题（本大题有7个小题，每小题10分，共70分.解答应写出文字说明、证明过程或演算步骤）
19.先化简，再求值：，其中是不等式组的整数解.
20.如图，平行四边形的对角线交于点O，分别以，为邻边作平行四边形，交于点F，连结.
（1）求证：F为中点；
（2）若，，求平行四边形的周长.
21.病毒虽无情，人间有大爱200年，在湖北省抗击新冠病毒的战“疫”中，全国（除湖北省外）共有30个省（区、市）及军队的医务人员在党中央全面部署下，白衣执甲，前赴后继支援湖北省.全国30个省（区、市）各派出支援武汉的医务人员频数分布直方图（不完整）和扇形统计图.如图所示：（数据分成6组：）


据新华网报道，在支援湖北省的医务人员大军中，有“90后”也有“00后”，他们是青春的力量，时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据：
C市派出的1614名医务人员中有404人是“90后”； H市派出的338名医务人员中有103人是“90后”； B市某医院派出的148名医务人员中有83人是“90后”.
根据以上信息回答问题
（1）补全频数分布直方图；
（2）求扇形统计图中派出人数大于等于100小于500所占扇形圆心角度数；
（3）请你根据小华得到的这些数据估计在支援湖北省的全体医务人员（按42万人计）中，“90后”有多少万人.（写出计算过程，结果精确到0.1万人）
22.阅读下列材料解答问题：
新定义：对非负数x“四舍五入”到个位的值记为，即：当n为非负整数时，如果，则；
反之，当n为非负整数时，如果，则.
例如：.试解决下列问题：
（1）①__________（π为圆周率）；
②如果，则数x的取值范围为_____________；
（2）求出满足的x的取值范围.
23.如图，中，，顶点都在反比例函数的图象上，直线轴，垂足为，连结，并延长交于点，当时，点恰为的中点，若.

（1）求反比例函数的解析式；
（2）求的度数.
24.某商场柜台销售每台进价分别为160元、120元的两种型号的电风扇，下表是近两周的销售情况：
（进价、售价均保持不变，）
（1）求两种型号的电风扇的销售单价；
（2）若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台；
（3）在（2）的条件下，商场销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由.
25.如图，在平面直角坐标系中，抛物线与轴正半轴交于点，且点的坐标为，过点作垂直于轴的直线是该抛物线上的任意一点，其横坐标为，过点作于点Q；是直线上的一点，其纵坐标为.以为边作矩形.

（1）求的值；
（2）当点与点重合时，求的值；
（3）当矩形是正方形，且抛物线的顶点在该正方形内部时，求的值；
（4）当抛物线在矩形内的部分所对应的函数值随的增大而减小时，直接写出的取值范围.
四、解答题（本大题有1个小题，共8分.解答应写出文字说明、证明过程或演算步骤）
26.如图，在等边三角形ABC中，BC=8，过BC边上一点P，作，分别与边AB，AC相交于点D与点E.
（1）在图中找出与∠EPC始终相等的角，并说明理由；
（2）若△PDE为正三角形时，求的值；
（3）当时，请用BP表示BD，并求出BD的最大值.










答案以及解析
一、选择题
1.答案：B
解析：2019的倒数是，的相反数是.
2.答案：C
解析：长方形绕它的一条所在的直线旋转一周后得到一个圆柱.
3.答案：A
解析：，解得.故选A.
4.答案：B
解析：切于点.，
.
5.答案：D
解析：本题考查整体法求代数式的值.原式，故选D.
6.答案：D
解析：由位似图形的画法可得:4个图形都是的位似图形.故选D.
7.答案：C
解析：5.5万.设这批电话手表有x块.根据题意，得，解得，所以这批电话手表至少有105块.
8.答案：B
解析：由图可得，芍药的数最为，所以当时，芍药的数量为.
9.答案：A
解析：本题考查三角函数的实际应用.过点C作于点F，由题意得，，，
.故选A.

10.答案：B
解析：，
解①得，
解②得，
∴不等式组的解集是．
∵不等式组有解，
∴，
∴．
解分式方程，得，
∵关于的分式方程有正数解，
∴是正数，
∴，
∵，
∴且，
综上：且．
∵为整数，
∴或2．
所有符合条件的整数的个数为2．
故选：B．
11.答案：B
解析：如图，连接.

平分，
，
，
.
平分垂直平分,
.故选B.
12.答案：C
解析：设点，则
因为M，N两点在反比例函数的图象上，

解得所以点.再作关于x轴的对称点，连接，交x轴于点P，此时的值最小.的最小值.故选C.
二、填空题
13.答案：
解析：
14.答案：
解析：本题考查用科学记数法表示较小的数.根据题意，.
15.答案：
解析：本题考查概率的计算.由题意得，从袋子8中随机取出1个球有8种等可能的结果，其中是红球的结果有3种，是红球的概率是.
16.答案：
解析：，,，
，
又绕A点逆时针旋转30°后得到，
，
17.答案：630
解析：设甲车，乙车的速度分别为x千米/时，y千米/时，
甲车与乙车相向而行5小时相遇，则，解得，
相遇后当甲车到达B地时两车相距720千米，
所需时间为小时，
则甲车从A地到B需要9小时，
故甲车的速度为千米/时，
乙车的速度为千米/时，
乙车行驶千米所需时间为小时，
甲车从B地到A地的速度为千米/时.
所以甲车从B地向A地行驶了=千米，
当乙车到达A地时，甲车离A地的距离为千米.
18.答案：8
解析：设签字笔购买了x支，则圆珠笔购买了支，
根据题意解不等式组得
是整数，
三、解答题
19.答案：原式.
解①得，解②得，
原不等式组的解集为.
为整数，.
当时，原式.
20.答案：(1) ∵四边形是平行四边形
∵四边形是平行四边形
∴F为中点
(2)，
∴是直角三角形
∵F为中点，
∴
∵
∵.为的中位线
∴
∴平行四边形的周长为
21.答案：（1）.
补全的频数分布直方图如图所示：

（2）
即扇形统计图中派出人数大于等于100小于500所占扇形圆心角度数是.
（3）（万人）.
答：在支援湖北省的全体医务人员（按42万人计）中，“90后”大约有1.2万人.
22.答案：（1）①由题意可得.
②
（2）根据题意，可得为整数，
设为整数，
则，
，
，
，
，
则
23.答案：（1）轴，，
点在反比例函数图象上，
（2）为直角三角形，点为的中点，
.
.
.
轴，
轴.
.
.
24.答案：解：（1）设A种型号电风扇的销售单价为x元，B种型号电风扇的销售单价为y元，
则，解得.
答：A种型号电风扇的销售单价为200元，B种型号电风扇的销售单价为150元.
（2）设采购A种型号电风扇a台，
则，
解得：，
答：A种型号的电风扇最多能采购37台.
（3）能.
依题意，得：，
解得：，则，
是正整数，
或37，
能实现利润超过1850元的目标.
方案一：采购A种型号电风扇36台，B种型号电风扇14台；
方案二：采购A种型号电风扇37台，B种型号电风扇13台.
25.答案：（1）根据题意，得，解得.
（2）根据题意，得点的坐标为.
，
点的坐标为.
点与点重合，且点坐标为，
，
解得.
（3）将配方，得，
抛物线顶点的坐标为.
根据题意，得点坐标为.
如图1.
顶点在正方形的内部，
四边形是正方形，，
，
（舍去），，
的值为.
（4）当或时，抛物线在矩形内的部分所对应的函数值随的增大而减小.
【提示】如图2、图3.
四、解答题
26.答案：（1），理由见解析；
（2）8；
（3），的最大值为4.
解析：（1），
理由如下：为等边三角形，
是的外角，
，
；
（2）为正三角形，
，
在和中，
，
（3）为等边三角形，
为等边三角形，
∴，即
整理得，，
，
∴的最大值为4.销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元