

精品解析:安徽省安庆市桐城市第二中学2021-2022学年八年级上学期期末数学试题(原卷版)
展开一、选择题
1. 在平面直角坐标系中,点所在的象限是( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
2. 低碳环保理念深入人心,共享单车已成为出行新方式.下列共享单车图标,是轴对称图形的是( )
A. B. C. D.
3. 一次函数的图象经过两个点和,则,的大小关系是( )
A B. C. 当时D. 当时,
4. 若一个三角形的三个内角度数的比为2:3:4,则这个三角形是( )
A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形
5. 等腰三角形一边长为,周长是,则底边的长是( )
A. B. C. 7或D. 4或
6. 如图,直线EF经过AC中点O,交AB于点E,交CD于点F,下列不能使△AOE≌△COF的条件为( )
A. ∠A=∠CB. AB∥CDC. AE=CFD. OE=OF
7. 一次函数的图象与轴交于点,将一次函数图象绕着点转动,转动后得到的一次函数图象与两坐标轴所围成的面积比原来增加2,则转动后得到的一次函数图象与轴交点横坐标为( )
A. B. 3C. 3或D. 6或
8. 下列命题中,一定是真命题的是( )
A 同位角相等
B. 三角形中任何两边的和大于第三边
C. 三角分别相等的两个三角形全等
D. 直线向下平移2个单位可得到一次函数的图象
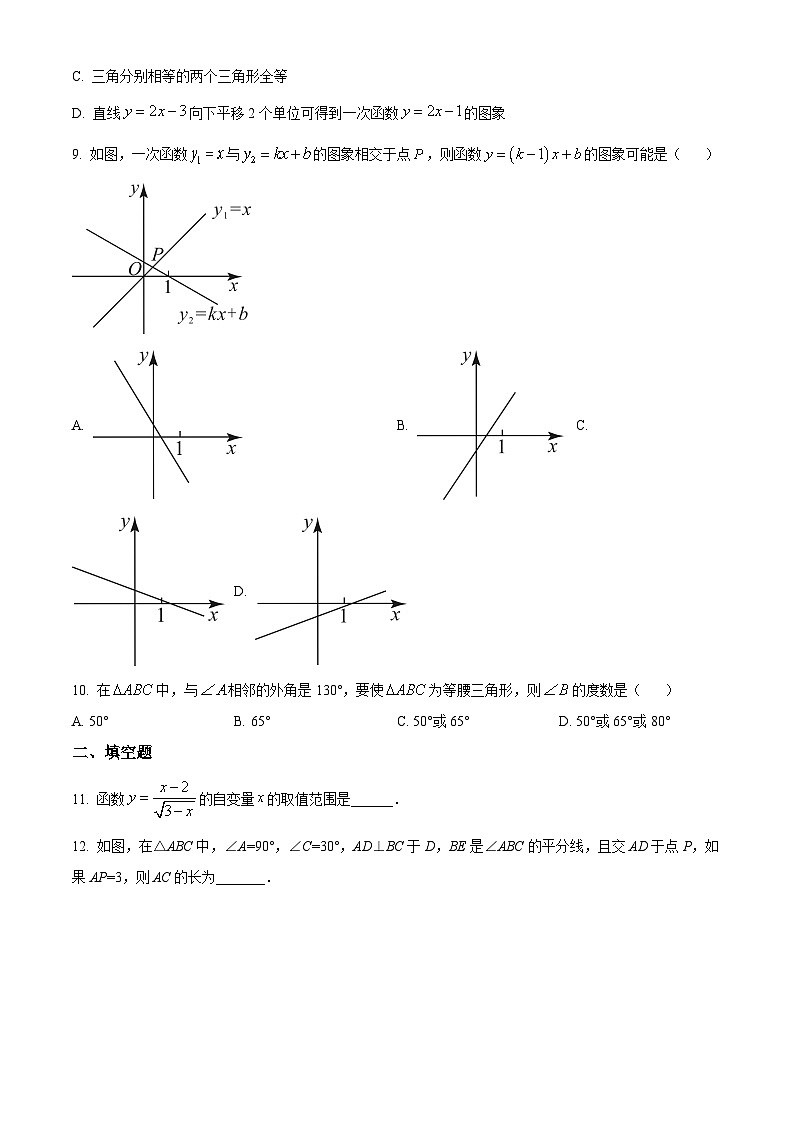
9. 如图,一次函数与的图象相交于点,则函数的图象可能是( )
A. B. C. D.
10. 在中,与相邻的外角是130°,要使为等腰三角形,则的度数是( )
A. 50°B. 65°C. 50°或65°D. 50°或65°或80°
二、填空题
11. 函数的自变量的取值范围是______.
12. 如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于点P,如果AP=3,则AC的长为_______.
13. (1)如图是正方形网格,其中已有3个小方格涂成了黑色,请在图中13个白色小方格中选出一个也涂成黑色,使黑色的图形成为轴对称图形.
(2)满足(1)中条件的白色小方格共有______个.
14. 一次函数y=ax+3a+2(a为常数).请指出此图象必过一定点A的坐标________;平面内还有两点B(1,2),C(-2,1),此图象与线段BC有交点,直接写出a的取值范围___________.
三、计算题
15. 直线y=mx+n与y=2x+1相交于(1,b)点,与y=-x-2相交于(a,1)点,求m、n的值.
16. 如图,△ABC中,CA=CB,D是AB中点,∠B=42°,求∠ACD的度数.
四、解答题
17. 如图,在边长为个单位长度的小正方形网格中建立平面直角坐标系已知的顶点的坐标为,顶点的坐标为,顶点的坐标为.
(1)把向下平移个单位长度,再以轴为对称轴对称,得到,请你画出,并直接写出点,,的坐标;
(2)求的面积.
18. 如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证:△ACB≌△BDA;
(2)若∠CAB=54°,求∠CAO的度数.
19. 如图,一次函数l1:y=2x-2的图象与x轴交于点D,一次函数l2:y=kx+b的图象与x轴交于点A,且经过点B(3,1),两函数图象交于点C(m,2).
(1)求m,k,b的值;
(2)根据图象,直接写出1<kx+b<2x-2的解集.
20. (1)观察与发现
小明将三角形纸片沿过点的直线折叠,使得落在边上,折痕为,展开纸片(如图①);再次折叠该三角形纸片,使点和点重合,折痕为,与相交于点,展平纸片后得到(如图②).小明认为是等腰三角形,你同意吗?请说明理由.
(2)实践与运用
将长方形纸片沿过点的直线折叠,使点落在边上的点处,折痕为(如图③);再沿过点的直线折叠,使点落在上的点处,折痕为(如图④);再展平纸片(如图⑤).求图⑤中的大小.
21. 为了贯彻落实市委市政府提出的“精准扶贫”精神,某校特制定了一系列关于帮扶A,B两贫困村的计划,我决定从某地运送126箱鱼苗到A,B两村养殖,若用大、小费车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大、小货车的载货能力分别为10箱/辆和6箱/辆,其运往A,B两村的运费如下表:
(1)这15辆车中大、小货车各多少辆.
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前柱A,B两村总费用为y元,试求出y与x的函数表达式;
(3)在(2)的条件下,若运往A村的鱼苗不少于78箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
22. 如图,在四边形ABCD中,∠BAE=∠ACD=90°,BC=CE.
(1)∠BAC与∠D相等吗?为什么?
(2)E点在AD边上,若∠BCE=90°,试判断△ACD的形状,并说明理由.
23. 如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B=_____________°,∠C=_____________°;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
目的地
A村(元,辆-1)
B村(元,辆-1)
大货车
800
900
小货车
500
700
安徽省安庆市桐城市第二中学2023-2024学年九年级上学期期末数学试题: 这是一份安徽省安庆市桐城市第二中学2023-2024学年九年级上学期期末数学试题,共25页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
安徽省安庆市桐城市第二中学2023-2024学年八年级上学期期末数学试题: 这是一份安徽省安庆市桐城市第二中学2023-2024学年八年级上学期期末数学试题,共24页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
安徽省安庆市桐城市第二中学2023-2024学年七年级上学期期末数学试题(原卷+解析): 这是一份安徽省安庆市桐城市第二中学2023-2024学年七年级上学期期末数学试题(原卷+解析),文件包含精品解析安徽省安庆市桐城市第二中学2023-2024学年七年级上学期期末数学试题原卷版docx、精品解析安徽省安庆市桐城市第二中学2023-2024学年七年级上学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












