2022~2023学年苏州市吴江区梅震平教育集团八年级上学期月考数学试卷（第一次）（含解析）

这是一份2022~2023学年苏州市吴江区梅震平教育集团八年级上学期月考数学试卷（第一次）（含解析），共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、凤凰光学、太极股份和华为集团等就是其中的杰出代表，上述四个企业的标志是轴对称图形的是
A. B. C. D.
2.等腰三角形两边长分别为2和4，则这个等腰三角形的周长为
A. 6B. 10C. 8D. 8或10
3.下列各组数据中，不能作为直角三角形三边长的是
A. 9，12，15B. 3，4，5C. 6，8，11D. 40，41，9
4.如图，已知∠C=∠D=90∘,AC=AD，那么ΔABC与ΔABD全等的理由是
A. HLB. SASC. ASAD. AAS
5.如图，在△ABC中，AC的垂直平分线分别交AB,AC于点D,E,EC=5,△ABC的周长为26，则△BDC的周长为
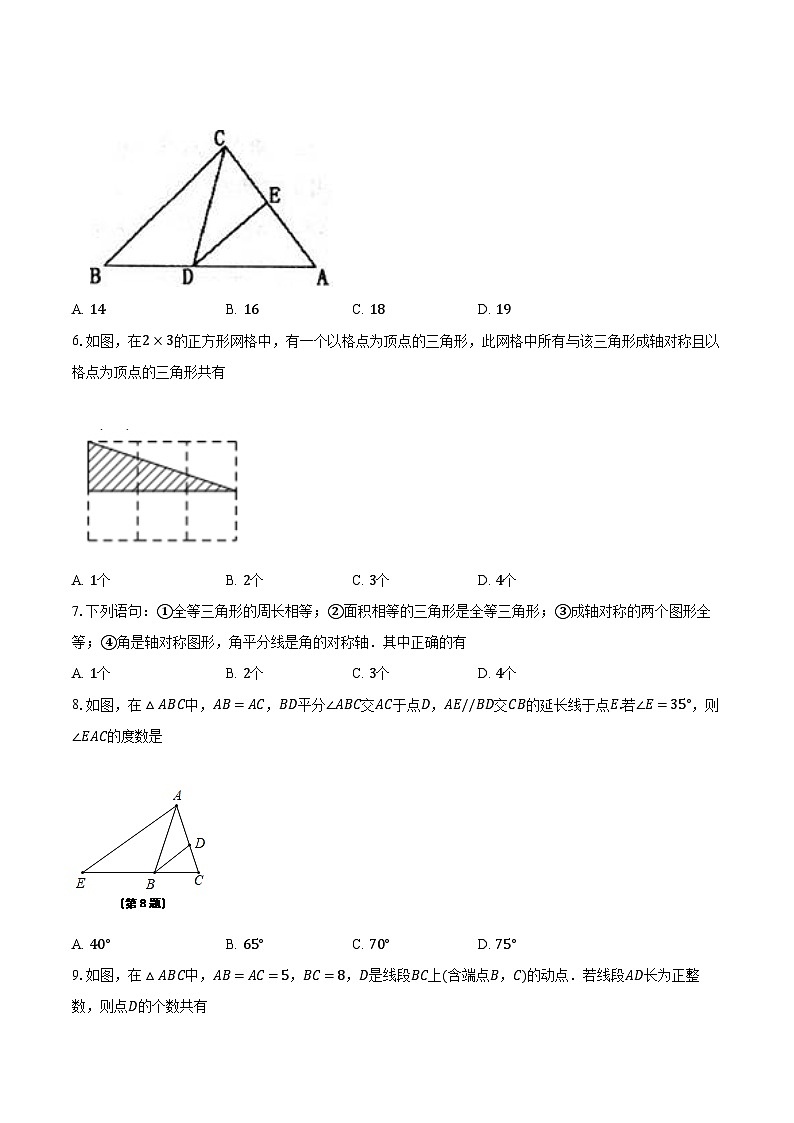
A. 14B. 16C. 18D. 19
6.如图，在2×3的正方形网格中，有一个以格点为顶点的三角形，此网格中所有与该三角形成轴对称且以格点为顶点的三角形共有
A. 1个B. 2个C. 3个D. 4个
7.下列语句：①全等三角形的周长相等；②面积相等的三角形是全等三角形；③成轴对称的两个图形全等；④角是轴对称图形，角平分线是角的对称轴．其中正确的有
A. 1个B. 2个C. 3个D. 4个
8.如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE//BD交CB的延长线于点E.若∠E=35°，则∠EAC的度数是
A. 40°B. 65°C. 70°D. 75°
9.如图，在△ABC中，AB=AC=5，BC=8，D是线段BC上(含端点B，C)的动点．若线段AD长为正整数，则点D的个数共有
A. 5个B. 4个C. 3个D. 2个
10.如图，点P、Q分别是边长为4cm的等边ΔABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，下面四个结论：①BP=CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60∘；④当第43秒或第83秒时，△PBQ为直角三角形．其中正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
二、填空题：本题共8小题，每小题3分，共24分。
11.等腰三角形的一个内角为100°，则它的底角为_ _°．
12.直角三角形的两直角边分别为15cm和20cm，则斜边上的高为_ _cm．
13.若直角三角形斜边上的高和中线长分别是4cm，6cm，则它的面积是_ _cm2．
14.如图，若∠1=∠2，加上一个条件 ，则有△AOC≌△BOC．
15.如图，在△ABC中，∠C=90°，点D，E分别在AC、AB上，BD平分∠ABC，DE⊥AB，AB=15，CD=4.△ABD的面积为_ _.
16.在《九章算术》中有一个问题(如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何？它的意思是：一根竹子原高一丈(10尺)，中部一处折断，竹梢触地面处离竹根3尺，试问折断处离地面 尺．
17.如图，△ABC和△ECD都是等腰直角三角形，∠BCA=∠DCE=90°，△ABC的顶点A在△ECD的斜边DE上．下列结论：①△ACE≌△BCD；②∠DAB=∠ACE；③AE+AC=CD；④△ABD是直角三角形．其中正确的是 (填写序号)．
18.如图，在△ABC中，∠ACB=90∘，∠A=30∘，AB=5，点P是AC上的动点，连接BP，以BP为边做等边△BPQ，连接CQ，则点P在运动过程中，线段CQ长度的最小值是 ．
三、解答题：本题共10小题，共80分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
如图，点E在线段AC上，BC//DE,AC=DE,CB=CE．
求证：∠A=∠D．

20.(本小题8分)
如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上．
(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′；
(2)四边形ABCA′的面积为 ；
(3)在直线l上找一点P，使PA+PB的值最小．(不写画法，需保留画图痕迹)
21.(本小题8分)
已知：如图，在△ABC中，AB=AC，AB的垂直平分线DE分别交AB、AC于D、E．
(1)若AC=12，BC=10，求△EBC的周长；
(2)若∠A=40°，求∠EBC的度数．
22.(本小题8分)
如图，已知BA⊥AC，CD⊥DB，AC与BD交于O，BD=CA.求证：
(1)BA=CD；
(2) △OBC是等腰三角形．
23.(本小题8分)
如图，一张长方开纸片宽AB=8cm，长BC=10cm.现将纸片折叠，使顶点D落在边BC上的点F处(折痕为AE)，求EC的长．(注：长方形的对边平行且相等，四个角都是直角)
24.
(1)【方法探究】我们知道，通过不同的方法表示同一图形的面积可以探求相应的数量关系．如图1，它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形，直角三角形的两条直角边长分别为a、b(a(2)【方法迁移】将图1中的四个形状大小完全相同的直角三角形拼成图2，a，b，c之间仍然具有以上数量关系吗?请在图2中添加适当的辅助线，并加以说明．
25.(本小题8分)
如图，AD是△ABC的高，CE是△ABC的中线．
(1)若AD=12，BD=16，求DE；
(2)已知点F是中线CE的中点，连接DF，若∠AEC=57°，∠DFE=90°，求∠BCE的度数．
26.(本小题8分)
有一台风中心沿东西方向AB由点A行驶向点B，已知点C为一海港，且点C与直线AB上两点A、B的距离分别为300km和400km，又AB=500km，以台风中心为圆心周围250km以内为受影响区域．
(1)海港C会受台风影响吗？为什么？
(2)若台风的速度为20km/h，台风影响该海港持续的时间有多长？
27.(本小题8分)
在Rt△ABC中，AC=BC，∠ACB=90°，P为线段AB上一动点．
(1)如图1，点D、E分别在AC、BC上(点D不与点A重合)，若P运动到AB的中点，且PD⊥PE．
①求证：AD=CE．
②若AD=7，BE=1，求PD的长．
(2)如图2，点F在BC上，且PC=PF，过点F作FH⊥AB，垂足为H，若AB=8，在点P运动的过程中，线段PH的长度是否发生变化？若不变，请求出PH的长度；若变化，请说明理由．
28.(本小题8分)
如图①，在长方形ABCD中，已知AB=13，AD=5，动点P从点D出发，以每秒1个单位的速度沿线段DC向终点C运动，运动时间为t秒，连接AP，把△ADP沿着AP翻折得到△AEP.(注：长方形的对边平行且相等，四个角都是直角)
(1)如图②，射线PE恰好经过点B，求出此时t的值；
(2)当射线PE与边AB交于点F时，是否存在这样的t的值，使得FE=FB？若存在，请求出所有符合题意的t的值；若不存在，请说明理由；
(3)在动点P从点D到点C的整个运动过程中，若点E到直线AB的距离等于3，则此时t= ．
答案和解析
1.【答案】D
【解析】略
2.【答案】B
【解析】略
3.【答案】C
【解析】略
4.【答案】A
【解析】略
5.【答案】B
【解析】略
6.【答案】C
【解析】略
7.【答案】B
【解析】略
8.【答案】D
【解析】略
9.【答案】A
【解析】略
10.【答案】C
【解析】略
11.【答案】40
【解析】略
12.【答案】12
【解析】略
13.【答案】24
【解析】略
14.【答案】∠A=∠C(或AO=BO或∠ACO=∠BCO)
【解析】略
15.【答案】30
【解析】略
16.【答案】4.55
【解析】略
17.【答案】①②④
【解析】略
18.【答案】54
【解析】略
19.【答案】证明：∵BC // DE，∴∠BCA=∠CED，
又∵AC=DE，CB=CE，
∴△ABC≌△DCE(SAS)，
∴∠A=∠D．

【解析】见答案
20.【答案】【小题1】
略
【小题2】
8.5
【小题3】
略

【解析】1. 略
2.
略
3. 连接点A和点Bˈ，与直线l的交点就是点P．
21.【答案】【小题1】△EBC的周长为22；
【小题2】∠EBC的度数为30°．

【解析】1. 略
2. 略
22.【答案】【小题1】
∵BA⊥AC，CD⊥DB∴∠A=∠D=90°，
在Rt△ABC和Rt△DCB中AC=DBBC=CB，∴△ABC≌△DCB (HL)，∴BA=CD，
【小题2】∵△ABC≌△DCB∴∠ACB=∠DBC，∴BO=CO，∴△OBC是等腰三角形．

【解析】1. 见答案
2. 见答案
23.【答案】∵四边形ABCD是矩形，AB=8cm，BC=10 cm，
∴AB=CD=8 cm，AD=BC=10 cm.
设EC=x cm，则DE=(8−x) cm.
由折叠性质可知，EF=ED=8−x，AF=AD=10 cm.
∵在Rt△ABF中，BF=6 cm，∴CF=BC−BF=4 cm.
∵在Rt△CEF中，CF2+CE2=EF2，∴42+x2=(8−x)2，解得x=3，∴EC=3 cm.

【解析】见答案
24.【答案】【小题1】
(a+b)2
c2 +2ab
a2+b2=c2
【小题2】
由a2+b2+ab=c2+ab得a2+b2=c2

【解析】1. 略
2. 略
25.【答案】【小题1】
∵AD⊥BC，∴∠ADB=90°，∴AB=20，
∵CE是中线，∴DE是斜边AB上的中线，∴DE= 12 AB=10；
【小题2】
∵DF⊥CF，F是CF的中点，∴DE=DC，∴∠DEC=∠DCE，
∴∠EDB=∠DEC+∠DCE=2∠BCE，
∵DE=BE，∴∠B=∠EDB，∴∠B=2∠BCE，
∴∠AEC=3∠BCE=57°，则∠BCE=19°．

【解析】1. 见答案
2. 见答案
26.【答案】【小题1】
海港C受台风影响。
理由：如图，过点C作CD⊥AB于D，
∵AC=300km，BC=400km，AB=500km，
∴AC2+BC2=AB2.∴△ABC是直角三角形。
∴AC×BC=CD×AB∴300×400=500×CD∴CD=240(km)
∵以台风中心为圆心周围250km以内为受影响区域，∴海港C受到台风影响。
【小题2】
当EC=250km，FC=250km时，正好影响C港口，
∵ED=70(km)，∴EF=140km
∵台风的速度为20km/h，∴140÷20=7(小时)
即台风影响该海港持续的时间为7小时。

【解析】1. 见答案
2. 见答案
27.【答案】【小题1】
①连接CP，证△ADP≌△CEP
②连接DE，AC=CB=8，CD=1，根据勾股定理得DE2=50，所以DP2=25，所以DP=5
【小题2】作CQ⊥AB，垂足为Q，证△CPQ≌△PFH，可得PH=CQ=4

【解析】1. 见答案
2. 略
28.【答案】【小题1】
情况①点E在长方形ABCD内，
∵△ADP沿着AP翻折得到△AEP∴PD=PE=t，∠APD=∠APE．
∵长方形ABCD，AD=13 ∴AD // BC∴∠APD=∠PAB
∴ BP=AB=13．
∵CB=5，∠C=90°∴CP=12
∴ DP=CD−CP=1∴t =1．
【小题2】
点E在长方形ABCD内，设BF=EF= x，则AF= 13−x．
∵∠AEF=90°，AE=5，∴FC2=EF2+EC2
即(13−x)2= x 2+52 解之得：x =7213．
由(1)可知PF=AF=13−x
∴PE=PF−EF=(13−x)−x =13−2 x =13−2×7213 =2513
∴t =2513．
情况②，点E在长方形ABCD外，
设BF=EF= x，则AF= 13−x
由(1)可知PF=AF=13−x
∴PE=PF+EF=(13−x) +x =13
∴t =13
综上所述t的值为2513或13
【小题3】
52或10

【解析】1. 见答案
2. 见答案
3. 略