人教版九年级下册27.2.1 相似三角形的判定课文内容ppt课件

这是一份人教版九年级下册27.2.1 相似三角形的判定课文内容ppt课件，文件包含272教学课件相似三角形第2课时pptx、272教学设计相似三角形第2课时docx、272练习·基础巩固相似三角形第2课时docx、272练习·素能拓展相似三角形第2课时docx、272练习·能力提升相似三角形第2课时docx、272预习导学相似三角形第2课时docx等6份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

　　1．全等三角形与相似三角形有怎样的关系？
　　全等三角形是相似比为 1 的相似三角形，即全等三角形是特殊的相似三角形，而相似三角形不一定是全等三角形．
　　基本事实：两条直线被一组平行线所截，所得的对应线段成比例．
　　2．平行线分线段成比例的基本事实及推论分别是什么？
　　推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．
　　3．上节课学习了哪些判定三角形相似的方法？
　　定义法：三个角分别相等，三条边成比例的两个三角形相似．
　　利用平行线判定三角形相似：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似．
　　判定三角形全等的方法有哪些？
　　SSS，SAS，AAS，ASA，HL．
　　类似于判定三角形全等的 SSS 方法，我们能不能通过三边来判定两个三角形相似呢？
　　任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的 k 倍，度量这两个三角形的角，它们分别相等吗？这两个三角形相似吗？
　　通过度量可知，两个三角形的对应角相等；又由题意可知，两个三角形的边对应成比例，所以这两个三角形相似．
　　猜想：三边成比例的两个三角形相似．
　　你能证明这个猜想吗？
　　证明：在线段 A′B′（或它的延长线）上截取 A′D＝AB， 过点 D 作 DE∥B′C′，交 A′C′ 于点 E．
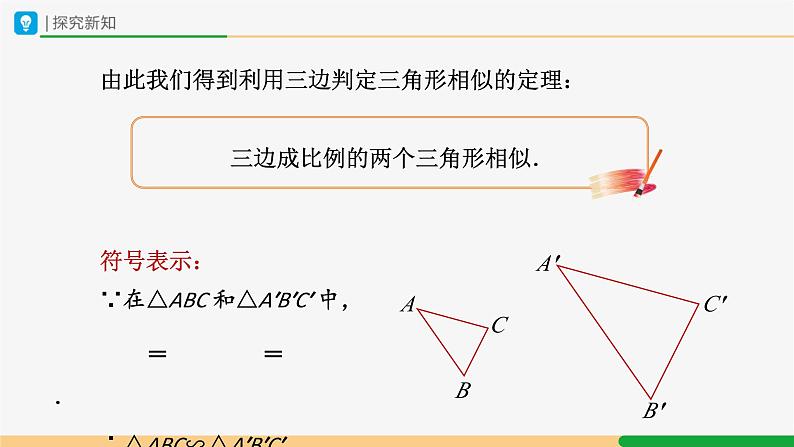
　　由此我们得到利用三边判定三角形相似的定理：
　　类似于判定三角形全等的 SSS 方法，我们证明了三边对应成比例的两个三角形相似．那么类似于判定三角形全等的 SAS 方法，能不能通过两边和夹角来判定两个三角形相似呢？
　　任意画一个△ABC，再画一个△A′B′C′，使∠A＝∠A′， ＝
＝k，量出 BC 及 B′C′ 的长，它们的比值等于 k 吗？再量一量
这两个三角形另外两组角，它们分别相等吗？这两个三角形相似吗？
　　通过度量可知，∠B＝∠B′，∠C＝∠C′，所以这两个三角形相似．
　　猜想：两边成比例且夹角相等的两个三角形相似．
　　由此我们得到利用两边和夹角判定三角形相似的定理：
　　对于△ABC 和△A′B′C′，如果 ＝ ，∠B＝∠B′，这两个三角形一定相似吗？
　　如图，△ABC 与△A′B′C′ 相似；△ABC 与△A′B′C′′ 不相似．
　　例1　根据下列条件，判断△ABC 和 △A′B′C′ 是否相似，并说明理由：　　AB＝4 cm，BC＝6 cm，AC＝8 cm，　　A′B′＝12 cm，B′C′＝18 cm，A′C′＝24 cm．
利用三边成比例判定三角形相似的步骤　　第 1 步：排序，即将三角形的边按大小顺序排列；　　第 2 步：计算，即分别计算三边的比值；　　第 3 步：判断，即看比值是否相等来判断两个三角形是否相似．
　　例2　根据下列条件，判断△ABC 和 △A′B′C′ 是否相似，并说明理由：　　∠A＝120°，AB＝7 cm，AC＝14 cm，　　∠A′＝120°，A′B′＝3 cm ，A′C′＝6 cm．
利用两边和夹角判定三角形相似的方法　　（1）找到两个三角形中相等的角；　　（2）分别找到两个三角形中夹这个等角的两条边，并按大小顺序排列；　　（3）看这两组边是否成比例，若成比例，则两个三角形相似，否则不相似．
相似三角形的判定（1）
由两边和夹角判定三角形相似的定理
由三边判定三角形相似的定理