

冀教版八年级上册16.3 角的平分线多媒体教学课件ppt
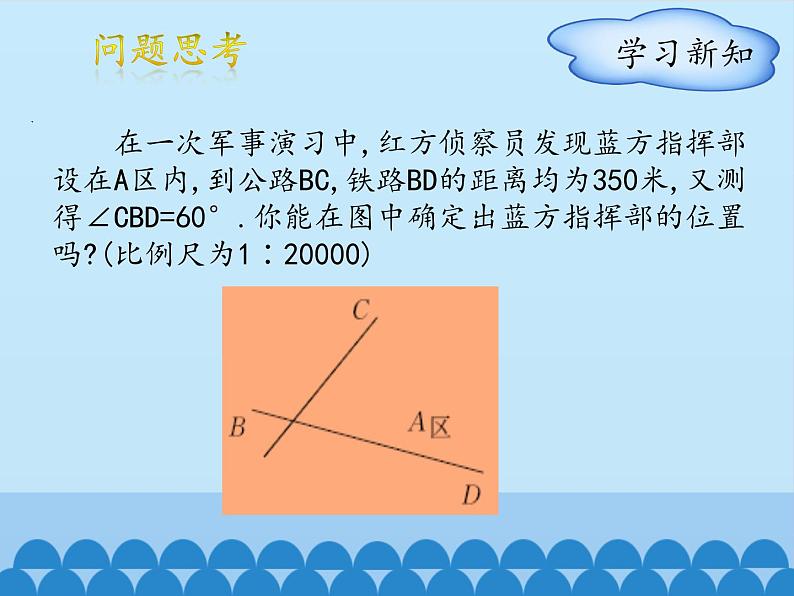
展开在一次军事演习中,红方侦察员发现蓝方指挥部设在A区内,到公路BC,铁路BD的距离均为350米,又测得∠CBD=60°.你能在图中确定出蓝方指挥部的位置吗?(比例尺为1∶20000)
活动一:角平分线的性质定理及其逆定理
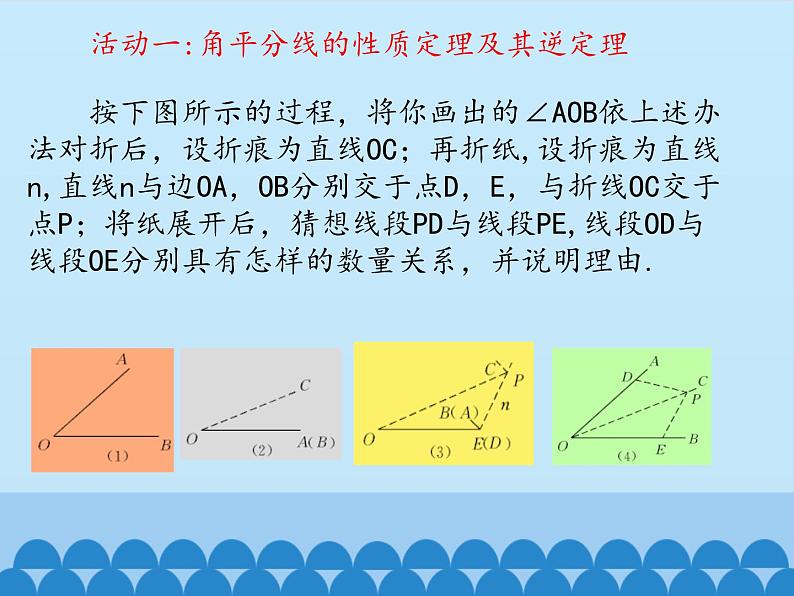
按下图所示的过程,将你画出的∠AOB依上述办法对折后,设折痕为直线OC;再折纸,设折痕为直线n,直线n与边OA,OB分别交于点D,E,与折线OC交于点P;将纸展开后,猜想线段PD与线段PE,线段OD与线段OE分别具有怎样的数量关系,并说明理由.
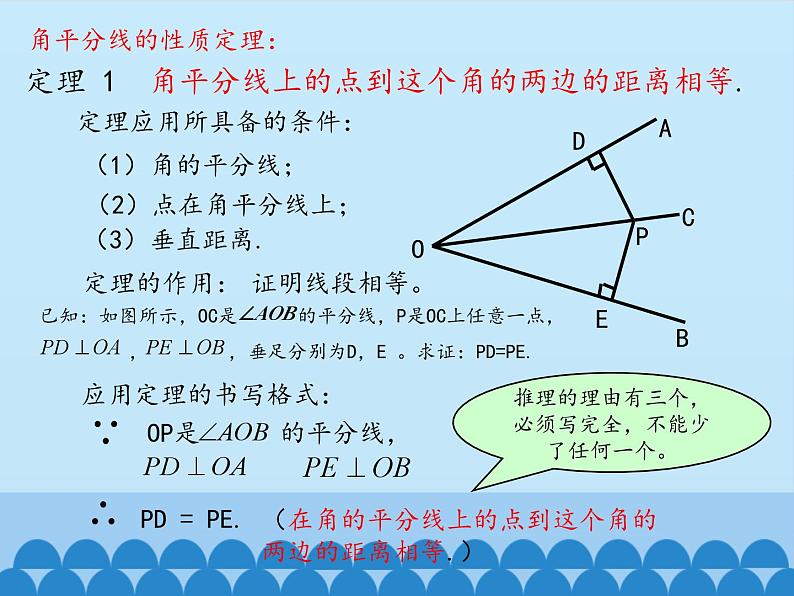
定理 1 角平分线上的点到这个角的两边的距离相等.
定理应用所具备的条件:
(在角的平分线上的点到这个角的两边的距离相等.)
推理的理由有三个,必须写完全,不能少了任何一个。
已知:如图所示,OC是 的平分线,P是OC上任意一点, , ,垂足分别为D,E 。求证:PD=PE.
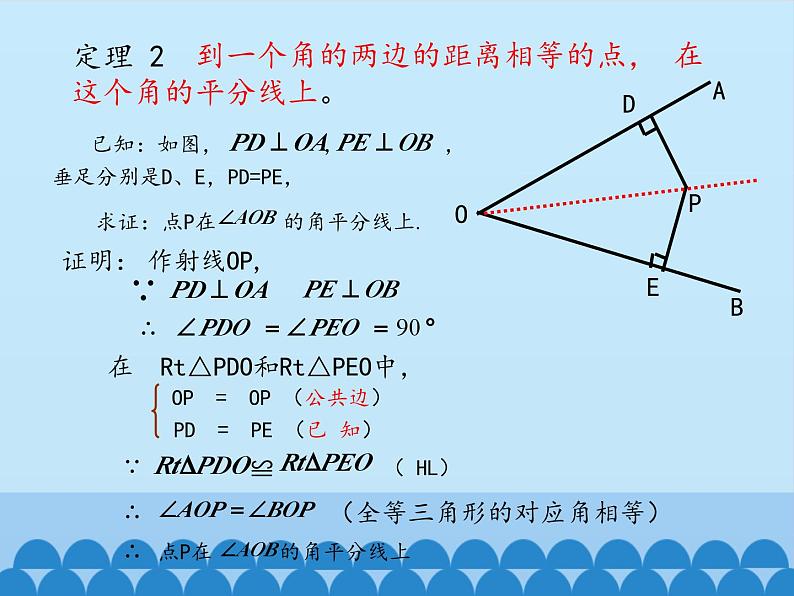
到一个角的两边的距离相等的点, 在这个角的平分线上。
在 Rt△PDO和Rt△PEO中,
(全等三角形的对应角相等)
OP = OP (公共边)
PD = PE (已 知)
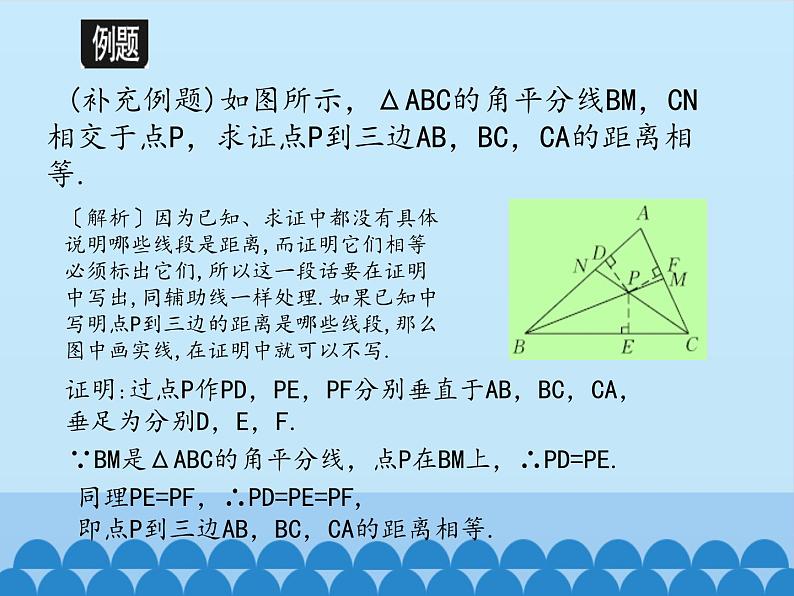
(补充例题)如图所示,ΔABC的角平分线BM,CN相交于点P,求证点P到三边AB,BC,CA的距离相等.
〔解析〕因为已知、求证中都没有具体说明哪些线段是距离,而证明它们相等必须标出它们,所以这一段话要在证明中写出,同辅助线一样处理.如果已知中写明点P到三边的距离是哪些线段,那么图中画实线,在证明中就可以不写.
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足为分别D,E,F.
∵BM是ΔABC的角平分线,点P在BM上,∴PD=PE.
同理PE=PF,∴PD=PE=PF,即点P到三边AB,BC,CA的距离相等.
[知识拓展] 利用角的平分线的性质可直接推导出与角的平分线有关的两条线段相等,但在推导过程中不要漏掉垂直关系的书写,同时涉及角平分线上的点与角的两边的垂直关系时,可直接得到垂线段相等,不必再证两个三角形全等而走弯路.
[知识拓展] (1)角平分线的判定可帮助我们证明角相等,使证明过程简化.(2)角平分线可以看作是到角的两边距离相等的点的集合.(3)三角形的三条角平分线相交于一点,这点到三角形三边的距离相等.
活动二:角平分线的画法
3.作射线OC,则OC为所要求作的∠AOB的平分线.
1.以点O为圆心,适当长为半径画弧,分别交OA,OB于点D,E.
2.分别以点D,E为圆心,适当长为半径,在∠AOB的内部画弧,两弧相交于点C.
3.区别与联系:性质说明了角平分线上点的纯粹性,即:只要是角平分线上的点,那么它到此角两边一定等距离,无一例外;判定反映了角平分线的完备性,即只要是到角两边距离相等的点,都一定在角平分线上,绝不会漏掉一个.在实际应用中,前者用来证明线段相等,后者用来证明角相等(角平分线).
1.角的平分线的性质:角的平分线上的点到角的两边的距离相等.作用:直接证明两线段相等.使用的前提是有角的平分线,关键是图中是否有“垂直”.
2.角的平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.作用:证明角相等.
解析:过点D作DF⊥AC于F,∵AD是ΔABC中∠BAC的平分线,DE⊥AB,∴DE=DF,∵SΔABC=SΔABD+SΔACD,∴ 4×2+ AC×2=7,解得AC=3.故选A.
1.如图所示,AD是ΔABC中∠BAC的平分线,DE⊥AB于点E,SΔABC=7,DE=2,AB=4,则AC的长是 ( ) A.3 B.4 C.6 D.5
2.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列结论中不一定成立的是( ) A.PA=PBB.PO平分∠APBC.OA=OBD.AB平分OP
解析:∵OP平分∠AOB,PA⊥OA,PB⊥OB,∴PA=PB,∴ΔOPA≌ΔOPB,∴∠APO=∠BPO,OA=OB,∴A,B,C正确.设PO与AB相交于E.∵OA=OB,∠AOP=∠BOP,OE=OE,∴ΔAOE≌ΔBOE,∴∠AEO=∠BEO=90°,∴OP垂直于AB,而不能得到AB平分OP,故D不一定成立.故选D.
3.如图所示,在ΔABC中,角平分线AD,BE相交于O点,连接CO,则下列结论成立的是( ) A.ΔCEO≌ΔCDO B.OE=ODC.CO平分∠ACB D.OC=OD
解析:∵角平分线AD,BE相交于O点, ∴CO平分∠ACB.故选C.
解:如图所示,过点M作MD⊥AB于D,∵BC=16cm,CM∶MB=3∶5,∴CM= 16=6(cm),∵∠C=90°,AM平分∠CAB,∴DM=CM=6cm,即点M到AB的距离为6cm.
4.如图所示,ΔABC中,∠C=90°,AM平分∠CAB,BC=16cm,CM∶MB=3∶5,求点M到AB的距离.
解析:过点M作MD⊥AB于D,先求出CM,再根据角平分线上的点到角的两边距离相等可得DM=CM.
初中数学冀教版八年级上册16.3 角的平分线教学演示ppt课件: 这是一份初中数学冀教版八年级上册16.3 角的平分线教学演示ppt课件,共11页。PPT课件主要包含了复习回顾,小试牛刀,挑战自我,直击中考等内容,欢迎下载使用。
初中数学16.3 角的平分线教学课件ppt: 这是一份初中数学16.3 角的平分线教学课件ppt,文件包含教学课件八上·冀教·163角的平分线pptx、163docx等2份课件配套教学资源,其中PPT共39页, 欢迎下载使用。
初中数学冀教版八年级上册16.3 角的平分线课堂教学ppt课件: 这是一份初中数学冀教版八年级上册16.3 角的平分线课堂教学ppt课件,共18页。PPT课件主要包含了作射线OP,∴∠AOP∠BOP,符号语言,三角形的内角平分线,你能证明这个结论吗,角的平分线的性质,OP平分∠AOB,PD⊥OA于D,PE⊥OB于E,PDPE等内容,欢迎下载使用。














