沪科版七年级下册10.3 平行线的性质备课ppt课件

这是一份沪科版七年级下册10.3 平行线的性质备课ppt课件，共16页。PPT课件主要包含了导入新课，回顾与思考，讲授新课，∵a∥b已知，几何语言，总结归纳，应用格式，当堂练习，典例精析，看图填空等内容，欢迎下载使用。

问题 平行线的判定方法是什么？
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
利用练习本的横线格画两条平行线a//b，然后画一条截线c与a、b相交，标出如图的角. 任选一组同位角进行度量。
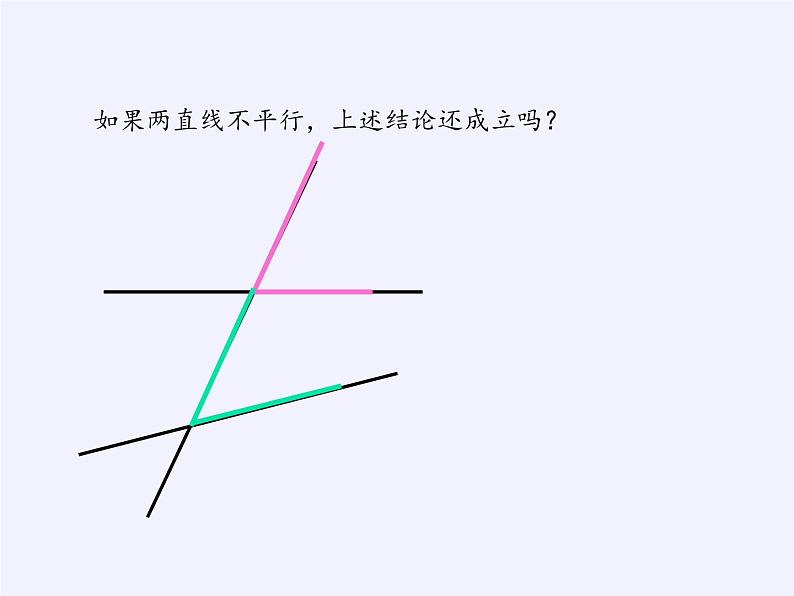
如果两直线不平行，上述结论还成立吗？
一般地，平行线具有性质：
性质1：两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等.
∴∠1=∠2 （两直线平行，同位角相等）
如图，已知a//b,那么2与3相等吗？为什么?
解∵ a∥b(已知), ∴∠1=∠2(两直线平行,同位角相等). 又∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换).
性质2：两条平行线被第三条直线所截，内错角相等。简单说成：两直线平行，内错角相等.
∴∠2=∠3 （两直线平行，内错角相等）
如图,已知a//b,那么2与4有什么关系呢？为什么?
解： ∵a//b （已知）,
∴ 1=  2（两直线平行，同位角相等）.
∵  1+  4=180°（邻补角）
∴ 2+  4=180°（等量代换）.
性质3：两条平行线被第三条直线所截，同旁内角互补。简单说成：两直线平行，同旁内角互补.
∴∠2+∠4=180 °（两直线平行，同旁内角互补）
1.如果有两条直线被第三条直线所截，那么必定有（ ） （A）内错角相等 (B)同位角相等（C）同旁内角互补 （D）以上都不对
2.∠1 和∠2是两条平行线被第三条直线所截形成的同旁内角,则 ( ) A. ∠1= ∠2 B. ∠1+∠2=90 C. ∠1+∠2=180 D .∠1是钝角, ∠2是锐角
例 如图，已知点D、E、F分别在△ABC的边AB,AC,BC上，且DE∥BC，∠B=48°（1）试求∠ADE的度数（2）如果∠DEF=48°，那么EF与AB平行吗？
（1）∵DE∥BC （已知）
∴∠ADE = ∠B = 48°（两直线平行，同位角相等）
（2）∵∠ADE=48°，∠DEF=48°（已知）
∴∠ADE = ∠DEF (等量代换)
∴EF∥AB (内错角相等，两直线平行)
（1）由DE∥BC，可以得到∠ADE=_______, 依据是____________________
（2）由DE∥BC，可以得到∠DFB=_______, 依据是____________________
（3）由DE∥BC，可以得到∠C+_______=180°, 依据是____________________
（4）由DF∥AC，可以得到∠AED=_______,依据是____________________
（5）由DF∥AC，可以得到∠AED=_______,依据是____________________
两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补
解: ∠A =∠D.理由：∵ AB∥DE( 　)∴∠A=_______ ( )∵AC∥DF( ) ∴∠D=______ ( )∴∠A=∠D ( )
2.如图1,若AB∥DE ,　AC∥DF，请说出∠A和∠D之间的数量关系，并说明理由。

两直线平行,同位角相等
解: ∠A+∠D=180. 理由：∵ AB∥DE( 　)∴∠A=__________ ( )∵AC∥DF( ) ∴∠D+ _______=180 ( )∴∠A+∠D=180（ ）
如图2,若AB∥DE ,　AC∥DF，请说出∠A和∠D之间的数量关系，并说明理由。
两直线平行,同旁内角互补
同位角相等内错角相等同旁内角互补