2022-2023学年安徽省宣城市七年级（上）期末数学试卷（含答案解析）

这是一份2022-2023学年安徽省宣城市七年级（上）期末数学试卷（含答案解析），共14页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.−2022的倒数是( )
A. 2020B. −2022C. 12022D. −12022
2.已知2amb2和−a5bn是同类项，则m+n的值为( )
A. 2B. 3C. 5D. 7
3.老旧小区改造是宣城市重点民生工程，市政府计划总投资额42892万元，其中“42892万”用科学记数法表示正确的是( )
A. 4.2892×104B. 4.2892×106C. 4.2892×108D. 4.2892×1010
4.下列方程的变形中，正确的是( )
A. 方程3x−2=2x+1，移项，得3x−2x=−1+2
B. 方程3−x=2−5(x−1)，去括号，得3−x=2−5x−1
C. 方程23x=32，未知数系数化为1，得x=1
D. 方程x−12−x5=1可化成5(x−1)−2x=10
5.学校为了了解家长对“禁止学生带手机进人校园”这一规定的意见，随机对全校300名学生家长进行调查，这一问题中样本是( )
A. 300B. 被抽取的300名学生家长
C. 被抽取的300名学生家长的意见D. 全校学生家长的意见
6.《孙子算经》是中国古代重要的数学著作．书中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，则可列方程为( )
A. 3x+3(100−x)=100B. x+3(100−x)=100
C. 3x+13(100−x)=100D. 3x+(100−x)=100
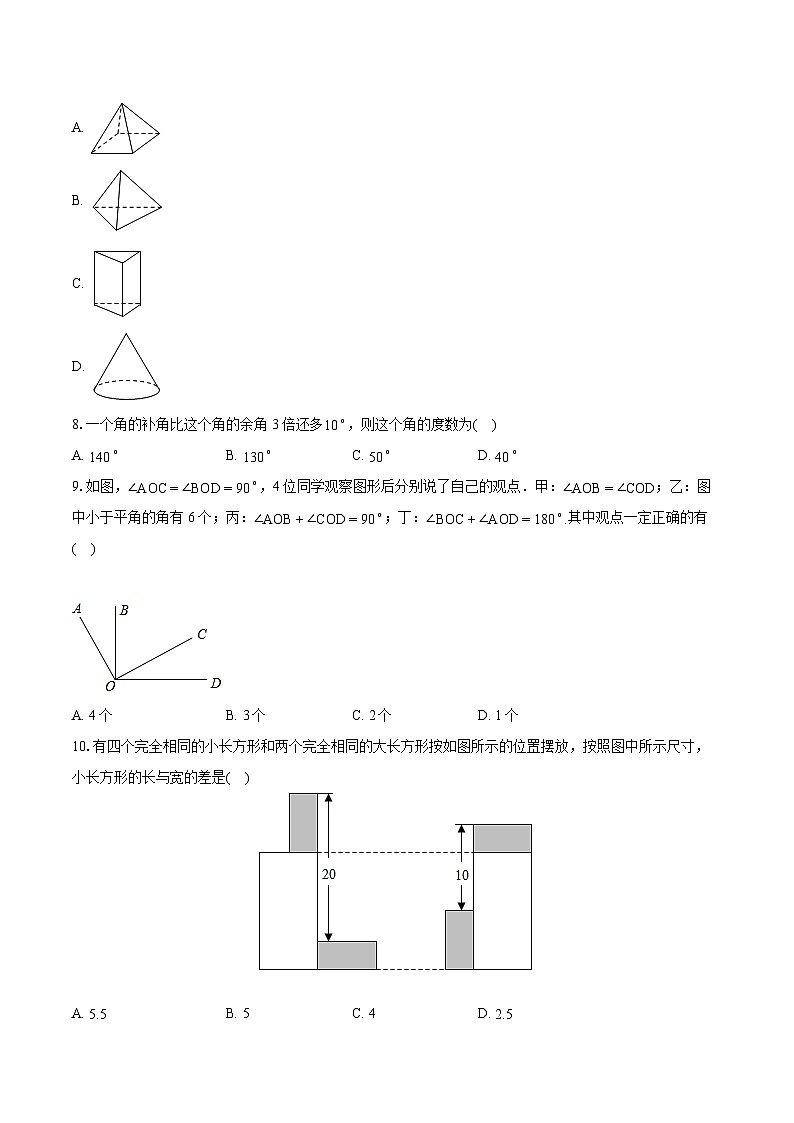
7.某立体图形的表面展开图如图所示，这个立体图形是( )
A.
B.
C.
D.
8.一个角的补角比这个角的余角3倍还多10∘，则这个角的度数为( )
A. 140∘B. 130∘C. 50∘D. 40∘
9.如图，∠AOC=∠BOD=90∘，4位同学观察图形后分别说了自己的观点．甲：∠AOB=∠COD；乙：图中小于平角的角有6个；丙：∠AOB+∠COD=90∘；丁：∠BOC+∠AOD=180∘.其中观点一定正确的有
( )
A. 4个B. 3个C. 2个D. 1个
10.有四个完全相同的小长方形和两个完全相同的大长方形按如图所示的位置摆放，按照图中所示尺寸，小长方形的长与宽的差是( )
A. 5.5B. 5C. 4D. 2.5
二、填空题（本大题共6小题，共18分）
11.比较大小：−8______ −7(填“<““>“)
12.若a、b互为相反数，则a−(5−b)的值为______ .
13.若(a+3)2+|b−2|=0，则ab=______。
14.一件商品如果按标价的八折销售，仍可获得20%的利润.已知该商品的成本价是40元，则该商品标价为______ 元.
15.如图是一个运算程序的示意图，若开始输入x的值为81，则第2023次输出的结果为______ .
16.在同一平面内，O为直线AB上一点，射线OE将平角∠AOB分成∠AOE、∠BOE两部分，已知∠BOE=α，OC为∠AOE的平分线，∠DOE=90∘，则∠COD=______.(用含有α的代数式表示)
三、计算题（本大题共2小题，共12分）
17.计算：−22−(4−5)3−8×|−12|.
18.解方程：2x−14=1−x+23.
四、解答题（本大题共5小题，共40分。解答应写出文字说明，证明过程或演算步骤）
19.(本小题6分)
先化简，再求值：12x−2(x−13y2)+(−32x+13y2)，其中x=−2，y=3.
20.(本小题6分)
如图，点B、C把线段AD分成2：5：3三部分，若点E为AD的中点，CE=6，求BE的长．
21.(本小题6分)
某医疗器械厂计划用600万元资金采购一批口罩生产机器，其中甲型机器每台的售价为10万元，乙型机器每台的售价为45万元.若购买甲型机器的数量是乙型机器数量的5倍还多3台，则甲、乙两种机器分别购入多少台？
22.(本小题10分)
生活垃圾的分类与回收利用可以减少污染，生活垃圾一般可分为四大类：可回收物(A)、厨余垃圾(B)、有害垃圾(C)和其他垃圾(D)，某垃圾处理厂统计了居民日常生活垃圾的分类情况，以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图．
请你根据上述统计图提供的信息，完成下列问题：
(1)求在此次调查中，表示“其他垃圾(D)”部分的扇形的圆心角的度数；
(2)请补全条形统计图；
(3)研究发现，在可回收物(A)中废纸约占15%，某企业利用回收的1吨废纸可生产0.8吨纸，若该市每天生活垃圾为4000吨，那么该企业每天利用回收的废纸可以生产多少吨纸？
23.(本小题12分)
如图，每个小正方形的面积均为1.将左图中黑色的小正方形移动，得到右边拼成的长方形，根据两种图形方法计算小正方形的个数；如图得出以下等式：
(1)请写出第3个等式：______ ；
(2)猜想第n个等式为：______ (用含n的等式表示)；
(3)当n为多少时，左图中的最底端有2024个小正方形？此时左图中共有多少个小正方形？
答案和解析
1.【答案】D
【解析】解：−2022的倒数是−12022，
故选：D.
乘积是1的两数互为倒数，由此即可得到答案．
本题考查倒数的概念，关键是掌握倒数的定义．
2.【答案】D
【解析】解：因为2amb2和−a5bn是同类项，
所以m=5，n=2，
所以m+n=5+2=7，
故选：D.
根据同类项的意义先求出m，n的值，然后再代入式子进行计算即可．
本题考查了同类项，熟练掌握同类项的意义是解题的关键．
3.【答案】C
【解析】解：42892万=428920000=4.2892×108.
故选：C.
绝对值大于1的数可以用科学记数法表示，一般形式为a×10n，n为正整数，且比原数的整数位数少1，据此可以解答．
本题考查用科学记数法表示较大的数，熟练掌握科学记数法表示较大的数一般形式为a×10n，其中1≤|a|<10，n是正整数，正确确定a的值和n的值是解题的关键．
4.【答案】D
【解析】【分析】
此题考查了解一元一次方程，解方程去分母时注意每项都乘以各分母的最小公倍数.各方程移项，去括号，未知数系数化为1，去分母分别得到结果，即可作出判断.
【解答】解：A.方程3x−2=2x+1，移项得：3x−2=1+2，不符合题意；
B.方程3−x=2−5(x−1)，去括号得：3−x=2−5x+5，不符合题意；
C.方程23x=32，未知数系数化为1，得：x=94，不符合题意；
D.方程x−12−x5=1化为5(x−1)−2x=10，符合题意.
故选D.
5.【答案】C
【解析】解：学校为了了解家长对“禁止学生带手机进人校园”这一规定的意见，随机对全校300名学生家长进行调查，这一问题中样本是被抽取的300名学生家长的意见，
故选：C.
总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，据此即可判断．
本题考查了样本的定义，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．
6.【答案】C
【解析】解：设大马有x匹，小马有(100−x)匹，由题意得：
3x+13(100−x)=100，
故选：C.
设大马有x匹，小马有(100−x)匹，根据题意可得等量关系：大马拉瓦数+小马拉瓦数=100，根据等量关系列出方程即可．
此题主要考查了由实际问题抽象出一元一次方程，关键是正确理解题意，找出题目中的等量关系，列出方程．
7.【答案】A
【解析】【分析】
本题考查了几何体的展开图，熟练掌握常见立体图形的平面展开图的特征，是解决此类问题的关键．利用立体图形及其表面展开图的特点解题．
【解答】
解：四个三角形和一个四边形，是四棱锥的组成，所以该立体图形的名称为四棱锥．
故选：A.
8.【答案】C
【解析】解：设这个角为α，则它的余角为90∘−α，补角为180∘−α，
根据题意得，180∘−α=3(90∘−α)+10∘，
180∘−α=270∘−3α+10∘，
解得α=50∘.
故选：C.
根据互为余角的两个角的和等于90∘，互为补角的两个角的和等于180∘，列出方程，然后解方程即可．
本题考查了互为余角与补角的性质，表示出这个角的余角与补角然后列出方程是解题的关键．
9.【答案】B
【解析】解：甲：因为∠AOC=∠BOD=90∘，所以∠AOB+∠BOC=∠BOC+∠COD=90∘，所以∠AOB=∠COD，故甲观点符合题意；
乙：图中小于平角的角有∠AOB，∠AOC，∠AOD，∠BOC，∠BOD，∠COD，共6个，故乙观点符合题意；
丙：∠AOB=∠COD，根据题意，无法得出∠AOB+∠COD=90∘，故丙观点不符合题意；
丁：∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=180∘，故丁观点符合题意，
故观点一定正确的有3个，
故选B.
10.【答案】B
【解析】解：设小长方形的长为x，宽为y，
根据题意得：20+y−x=10+x−y，即2x−2y=20−10，
整理得：x−y=5.
则小长方形的长与宽的差是5.
故选：B.
设小长方形的长为x，宽为y，根据题意由大长方形的长度相等列出方程求出x−y的值，即为小长方形的长与宽的差．
此题考查了二元一次方程的应用，解题关键是弄清题意，找到合适的等量关系，列出方程，注意整体思想的运用．
11.【答案】<
【解析】解：因为|−8|=8，|−7|=7，
所以−8<−7，
故答案为：<.
根据两个负数比较大小，其绝对值大的反而小比较即可．
本题考查了有理数的大小比较和绝对值的应用，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．
12.【答案】−5
【解析】解：因为a、b互为相反数，
所以a+b=0，
所以a−(5−b)
=a+b−5
=0−5
=−5.
故答案为：−5.
根据相反数的定义，可得a+b=0，然后去括号，再把a+b=0代入，即可求解．
本题主要考查了相反数的性质，去括号，求代数式的值，解题的关键是熟练掌握互为相反数的两数的和为0.
13.【答案】9
【解析】解：根据题意得，a+3=0，b−2=0，
解得a=−3，b=2，
所以，ab=(−3)2=9。
故答案为：9。
根据非负数的性质列式求出a,b的值，然后代入代数式进行计算即可得解。
本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0。
14.【答案】60
【解析】解：设该商品标价为x元，
依题意得：80%x−40=40×20%，
解得：x=60.
故答案为：60.
设该商品标价为x元，利用利润=售价-成本价，列出关于x的一元一次方程求解即可．
本题考查了由实际问题抽象出一元一次方程，解答本题的关键是明确题意，找出数量关系，列出方程．
15.【答案】3
【解析】解：因为第1次：13×81=27，
第2次：13×27=9，
第3次：13×9=3，
第4次：13×3=1，
第5次：1+2=3，
第6次：13×3=1，
…，
所以从第3次开始，奇数次运算输出的结果是3，偶数次运算输出的结果是1，
因为2023是奇数，
所以第2023次输出的结果为3，
故答案为：3.
根据运算程序进行计算，然后得到规律从第3次开始，奇数次运算输出的结果是3，偶数次运算输出的结果是1，然后解答即可．
本题考查了程序框图的计算，以及数字类规律探究．根据运算程序计算出从第3次开始，奇数次运算输出的结果是3，偶数次运算输出的结果是1是解题的关键．
16.【答案】12α或180∘−12α
【解析】解：①当射线OD，OE在直线AB的同侧时，如图所示：
因为OC为∠AOE的平分线，
所以∠1=∠2，
因为∠AOE+∠BOE=180∘，∠BOE=α，
所以∠AOE=180∘−α，
所以∠1=∠2=12(180∘−α)=90∘−12α，
所以∠COD=∠DOE+∠1=90∘+90∘−12α=180∘−12α；
②当射线OD、OE在直线AB的异侧时，如图所示：
因为OC为∠AOE的平分线，
所以∠1=∠2，
因为∠AOE+∠BOE=180∘，∠BOE=α，
所以∠AOE=180∘−α，
所以∠1=∠2=12(180∘−α)=90∘−12α，
所以∠COD=∠DOE−∠1=90∘−(90∘−12α)=12α.
综上所述，∠COD=12α或180∘−12α.
故答案为：12α或180∘−12α.
分两种情况：射线OD，OE在直线AB的同侧；射线OD，OE在直线AB的异侧；利用角平分线的定义，互补，角的和差关系即可求得结果．
本题考查了角平分线的定义，角的计算，考查了分类讨论的数学思想，要根据题意画出图形，分两种情况计算是解题的关键．
17.【答案】解：−22−(4−5)3−8×|−12|
=−4−(−1)3−8×12
=−4−(−1)−8×12
=−4+1−4
=−7.
【解析】先算乘方、绝对值与括号内的运算，再算乘除，最后算加减即可．
此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
18.【答案】解：去分母得：6x−3=12−4x−8，
移项合并得：10x=7，
解得：x=0.7.
【解析】方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．
19.【答案】解：12x−2(x−13y2)+(−32x+13y2)
=12x−2x+23y2−32x+13y2
=−3x+y2
当x=−2，y=3时，原式=−3×(−2)+32=15.
【解析】先去括号，再合并同类项，最后把x y的值代入求出即可．
本题考查了整式的加减-化简求值，主要考查学生的计算和化简能力．
20.【答案】解：设AB=2x，BC=5x，CD=3x，
所以AC=AB+BC=7x，AD=AB+BC+CD=10x，
因为点E为AD的中点，
所以AE=12AD=5x，
又CE=AC−AE=2x，CE=6，
所以2x=6，
解得x=3，
所以BC=5x=15，
所以BE=BC−CE=9.
故BE的长为9.
【解析】设AB=2x，BC=5x，CD=3x，求出AC=7x，AD=10x，根据点E为AD的中点求出AE=5x，由CE=AC−AE=2x，CE=6，列出方程，求出x，即可求出答案．
本题考查了求线段的长度，能用x表示各个线段的长度是解此题的关键．
21.【答案】解：设甲型机器购买x台，乙型机器购买y台，由题意得：
10x+45y=600x=5y+3，
解得：x=33y=6，
答：甲型机器购买33台，乙型机器购买6台．
【解析】根据两个等量关系：用600万元资金与甲型机器的数量是乙型机器数量的5倍还多3台，设甲型机器购买x台，乙型机器购买y台，列方程组解出即可．
本题考查了二元一次方程组的应用，根据题意找到等量关系列出方程是解题关键．
22.【答案】解：(1)本次调查的垃圾的总数量为：25÷25%=100(吨)，
表示“其他垃圾(D)”部分的扇形的圆心角的度数为：360∘×10100=36∘；
(2)“B”厨余垃圾的质量为：100−25−5−10=60(吨)，
补全条形统计图如下：
(3)4000×25100×15%×0.8
=1000×15%×0.8
=150×0.8
=120(吨)，
答：该企业每天利用回收的废纸可以生产120吨纸．
【解析】(1)先根据“A”部分的质量除以“A”部分所占比例得出本次调查的垃圾的总质量，“D”部分所对应的圆心角等于360∘乘“D”所占的比例；
(2)用抽查总吨数分别减去其它三类的质量，求出“B餐厨垃圾”的吨数，补全条形统计图；
(3)先求出“A”类垃圾的质量，进而得出“A”类垃圾中废纸的质量，再根据1吨废纸可生产0.8吨纸可得结果．
考查条形统计图、扇形统计图的制作方法，理清两个统计图中的数量关系式解决问题的关键．
23.【答案】(1)2+4+6+8=4×5;
(2)2+4+6+⋯+2(n+1)=(n+1)(n+2);
(3)因为最底端有2024个小正方形，
所以2(n+1)=2024，
解得：n=1011，
所以2+4+6+⋯+2024=1012×1013=1025156(个)
答：n=1011，共有1025156个小正方形．
【解析】解：(1)2+4+6+8=4×5；
(2)2+4+6+⋯+2(n+1)=(n+1)(n+2)；
(3)见答案.
(1)根据给出的等式写出答案即可；
(2)根据这3个等式写出答案即可；
(3)因为最底端有2024个小正方形，所以2(n+1)=2024，得出n的值，再计算有多少个小正方形即可．
本题考查图形的规律，根据给出的式子找到规律是解题的关键．