





青岛版九年级上册3.2 确定圆的条件课前预习课件ppt
展开通过证明过共线三点不能作圆的具体实例,体会反证法 的含义;
了解用反证法证明命题的一般步骤,发展逻辑思维能力.
知道证明一个命题除用直接证法外,还有间接证法;
我们知道,不在同一条直线上的三点确定一个圆.思考下面的问题:
(2)为什么过同一条直线上的三点不能作圆?怎样证明这个结论呢?与同学交流.
(1)如果A,B,C三点在同一条直线上,经过点A,B,C能作出一个圆吗?试一试.
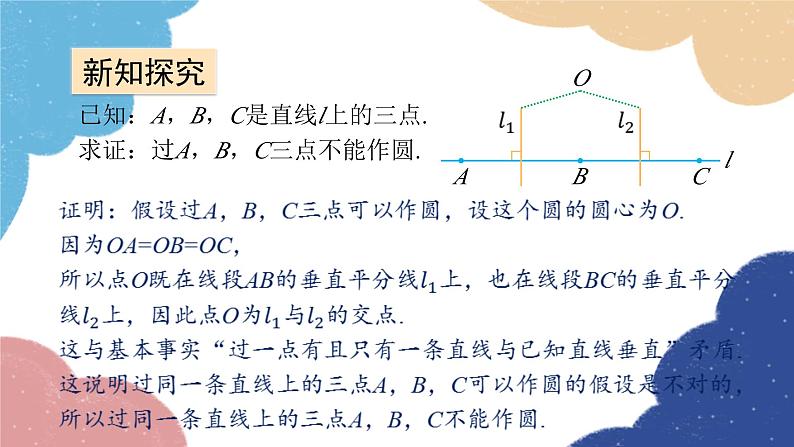
过同一条直线上的三点不能作圆.
已知:A,B,C是直线l上的三点.求证:过A,B,C三点不能作圆.
这种证明方法与我们以前学过的证明方法不同,它不是由已知条件出发直接证明命题的结论,而是
先提出与命题的结论相反的假设,推出矛盾,从而证明命题成立.
这种证明的方法叫做反证法.
当一个命题不易用直接证法证明时,可以考虑用反证法.
肯定结论----由矛盾判定假设不正确,从而肯定命题的结论正确.
用反证法证明一个命题,一般有三个步骤:
否定结论----假设命题的结论不成立;
推出矛盾----从假设出发,根据已知条件,经过推理论证,得出一个与命题的条件或已知的定义、基本事实、定理等相矛盾的结果;
用反证法证明“在△ABC中,若∠A>∠B>∠C,则∠A>60°”时,第一步应假设( )A.∠A=60° B.∠A<60° C.∠A≠60° D.∠A≤60°
解析:∠A与60°的大小关系有∠A>60°,∠A=60°,∠A<60°三种情况,因而,∠A>60°的反面是∠A≤60°.因此,用反证法证明“∠A>60°”时,应先假设∠A≤60°.
例1 证明平行线的性质定理1:两条平行线被第三条直线所截,同位角相等.已知:如图,直线AB∥CD,直线EF与AB,CD分别相交于点G,H.求证:∠1=∠2.
证明:假设∠1≠∠2.过点G作直线A′B′,使∠EGB′=∠2.根据基本事实“两条直线被第三条直线所截,如果同位角相等,那么两直线平行”,可得A′B′∥CD.
这样,过点G就有两条直线AB与A′B′与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.这说明∠1≠∠2的假设是不对的,所以∠1=∠2.
例2 证明:平行于同一条直线的两条直线平行.已知:如图,直线a∥c,b∥c.求证:a∥b.
证明:假设直线a,b不平行,那么它们相交,设交点为P.由已知a∥c,b∥c,这样过点P就有两条直线a,b与直线c平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.这说明a,b不平行的假设是不对的,所以a∥b.
1.用反证法证明“若⊙O的半径为r,点P到圆心的距离d大于r,则点P在⊙O的外部”,首先应假设( )A.d≤r B.点P在⊙O的外部 C.点P在⊙O上 D.点P在⊙O上或点P在⊙O的内部
2.用反证法证明:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等.
解:已知:在△ABC中,∠A≠∠B.求证:BC≠AC.证明:假设BC=AC,根据“等边对等角”,得∠A=∠B.这与已知∠A≠∠B相矛盾.这说明BC=AC的假设是错误的,所以BC≠AC.
3.用反证法证明:等腰三角形两底角必为锐角.
解:已知:△ABC是等腰三角形,∠B,∠C为底角.求证:∠B与∠C都是锐角.证明:①假设等腰三角形底角∠B,∠C都是直角,则∠B+∠C=180°,而∠A+∠B+∠C=180°+∠A>180°,这与三角形内角和等于180°矛盾;②假设等腰三角形的底角∠B,∠C都是钝角,则∠B+∠C>180°,
数学九年级上册3.4 直线与圆的位置关系教学课件ppt: 这是一份数学九年级上册3.4 直线与圆的位置关系教学课件ppt,共13页。PPT课件主要包含了学习目标,新知探究,新知精讲,典例精讲,方法总结,挑战自我,课堂小结,切线的判定定理,随堂练习等内容,欢迎下载使用。
初中青岛版1.4 图形的位似教学演示ppt课件: 这是一份初中青岛版1.4 图形的位似教学演示ppt课件,共19页。PPT课件主要包含了学习目标,复习导入,新知探究,例题讲解,随堂练习,-2-4,-2-4-6等内容,欢迎下载使用。
数学九年级上册3.3 圆周角评课ppt课件: 这是一份数学九年级上册3.3 圆周角评课ppt课件,共17页。PPT课件主要包含了学习目标,知识回顾,圆周角,圆周角定理,推论1,新知探究,反之亦然,新知精讲,典例精讲,挑战自我等内容,欢迎下载使用。













