山东省菏泽市郓城县2023-2024学年八年级上学期期中考试数学试题

这是一份山东省菏泽市郓城县2023-2024学年八年级上学期期中考试数学试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题给出的四个选项中，只有一个是正确的，把正确选项的代号填涂到答题卡上，每小题3分，共24分）
1.在实数-1.13，，0，，2.10010001，中，是无理数的有
A．4个B．3个C．2个D．1个
2.下列计算正确的是
A．3+=3 B．
C． D．
3.已知△ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是
第5题图
A．a2=b2-c2 B．a=6，b=8，c=10
C．∠A=∠B+∠C D．∠A:∠B:∠C=5:12:13
4.若一个直角三角形的三边长分别为：6，8，x，则x的值是
A．6 B．10 C．2 D．10或2
如图所示的是一所学校的平面示意图，若用(3，2)表示教学楼，
(4，0)表示旗杆，则实验楼的位置可表示成
A.(2，﹣3) B．(﹣2，1) C．(﹣3，2) D．(1，﹣2)
6.在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称．已知点
A1(1,2)，则点A2的坐标是
A．(-2,1) B．(-2,-1) C．(-1,-2) D．(-1,2)
7.下列平面直角坐标系中的图象，不能表示y是x的函数的是
A． B．C．D．
8.一次函数y1=ax+b与y2=bx+a，它们在同一坐标系中的大致图象是
A． B． C． D．
二、填空题（每小题3分，共18分）
9.16的算术平方根是 ．
10.如图，正方形OABC的边长为1，OA在数轴上，以原点O为圆心，对角线OB的长为半径画弧，交正半轴于一点D，则这个点D表示的实数是 ．
第10题图
11.一条直线y＝kx+b与直线y＝-2x+3平行，且经过点P（2，4），则该直线的表达式是 ．
12.已知点P（5a+1，6a+2）在一、三象限的角平分线上，则a＝ ．
13.如图，在等腰直角△ABC中，∠B=90°，AB=BC=1，过点C作DC⊥AC且DC=1，再过点D作ED⊥AD且ED=1，则AE的长为______.
第14题图
第13题图
14.如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合，则CD等于____cm．
解答题（共78分,解答要写出必要的文字说明、证明过程或演算步骤）
15.(6分）如图所示，两位同学为了测量风筝离地面的高度，测得牵线放风筝同学的头顶与风筝的水平距离为8米．已知牵线放风筝同学的身高为1.60米，放出的风筝线长度为17米（其中风筝本身的长宽忽略不计）,求此刻风筝离地面的高度；
第16题图
第15题图
16.（7分）如图，某小区有两个喷泉A，B，两个喷泉的距离长为250m．现要为喷泉铺设供水管道AM，BM，供水点M在小路AC上，供水点M到AB的距离MN的长为120m，BM的长为150m．
（1）求供水点M到喷泉A，B需要铺设的管道总长；
（2）求喷泉B到小路AC的最短距离．
17.（8分）计算：
(1) (2)
(3) (4)
18.（7分）已知一个正数的平方根分别是a-2和7-2a，3b+1的立方根是-2，c是的整数部分．
（1）求a，b，c的值；
（2）求5a+2b﹣c的平方根．
19.(8分）已知点P（2a-3，a+6），解答下列各题．
（1）点P在x轴上，求出点P的坐标；
（2）点Q的坐标为（3，3），直线PQ∥y轴，求出点P的坐标；
（3）若点P在第二象限，且它到x轴、y轴的距离相等，求a2023+2024的值．
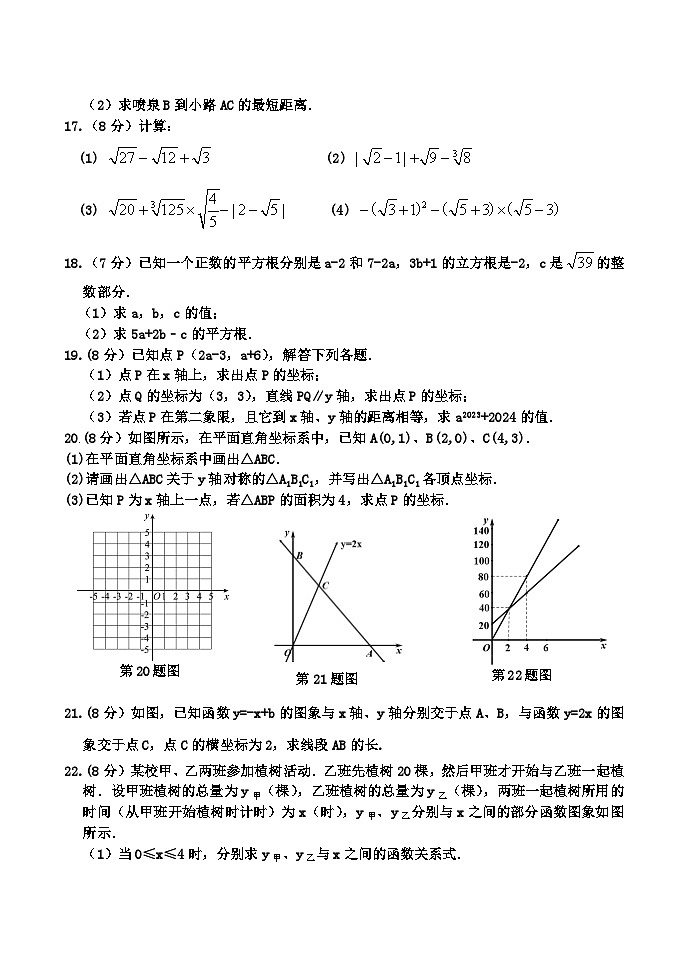
20.(8分）如图所示，在平面直角坐标系中，已知A(0,1)、B(2,0)、C(4,3)．
(1)在平面直角坐标系中画出△ABC．
(2)请画出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点坐标．
第22题图
(3)已知P为x轴上一点，若△ABP的面积为4，求点P的坐标．
第21题图
第20题图
21.(8分）如图，已知函数y=-x+b的图象与x轴、y轴分别交于点A、B，与函数y=2x的图象交于点C，点C的横坐标为2，求线段AB的长.
22.(8分）某校甲、乙两班参加植树活动．乙班先植树20棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为y甲（棵），乙班植树的总量为y乙（棵），两班一起植树所用的时间（从甲班开始植树时计时）为x（时），y甲、y乙分别与x之间的部分函数图象如图所示．
（1）当0≤x≤4时，分别求y甲、y乙与x之间的函数关系式．
（2）如果甲、乙两班均保持前4个小时的工作效率，通过计算说明，当x=6时，甲、乙两班植树的总量之和能否超过180棵．
23.(8分）先阅读，后解答：
；
像上述解题过程中，与、与相乘，积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化．
（1）的有理化因式是 ；的有理化因式是 ．
（2）将下列式子进行分母有理化：① ②
（3）类比（2）中②的计算结果，
计算：．
(10分）如图，直线AB与x轴交于点C，与y轴交于点B，已知点A(1,3),B(0,2).
(1)求直线AB的表达式．
(2)P为y轴上一点，若△ABP面积是△AOB面积的2倍，求点P坐标．
(3)在x轴上是否存在点Q，使得△AOQ为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
第24题图
2023——2024学年度八年级数学试题参考答案
一、选择题（每小题3分，共24分）
1、B 2、C 3、D 4、D 5、A 6、C 7、B 8、D
二、填空题（每小题3分，共18分）
4 10. 11.y=-2x+8 12.-1 13.2 14.3
三、解答题
15.解：（1）由题意得：BC＝17米，∠BDC＝90°，BD＝8米，DE＝1.60米，
在Rt△CDB中，由勾股定理得：
CD＝＝＝15（米），……………………………………………4分
∴CE＝CD+DE＝15+1.6＝16.6（米），
答：此刻风筝离地面的高度为16.6米；…………………………………………………6分
16.解：（1）在Rt△MNB中，BN＝＝＝90（m），
∴AN＝AB﹣BN＝250﹣90＝160（m），……………………………………………………2分
在Rt△AMN中，AM＝＝＝200（m），
∴供水点M到喷泉A，B需要铺设的管道总长＝200+150＝350（m）；…………………4分
（2）∵AB＝250m，AM＝200m，BM＝150m，
∴AB2＝BM2+AM2，
∴△ABM是直角三角形，
∴BM⊥AC，
∴喷泉B到小路AC的最短距离是BM＝150m．……………………………………………7分
17.解：（1）
＝3﹣2+
＝2；……………………………………………………………2分
（2）|﹣1|+﹣
＝﹣1+3﹣2
＝；……………………………………………………………2分
（3）
＝2+5×﹣（﹣2）
＝2+2﹣+2
＝3+2；……………………………………………………………2分
（4）
＝﹣（4+2）﹣（5﹣9）
＝﹣4﹣2+4
＝﹣2．……………………………………………………………2分
18.解：（1）∵一个正数的平方根是a﹣2和7﹣2a，
∴a﹣2+7﹣2a＝0，
解得：a＝5，………………………………………………………………2分
∵3b+1的立方根是﹣2，
∴3b+1＝﹣8，
解得：b＝﹣3，……………………………………………………………4分
∵36＜39＜49，
∴6<<7，
∴的整数部分是6，
∴c＝6，
∴a的值为5，b的值为﹣3，c的值为6；………………………………6分
（2）∵a的值为5，b的值为﹣3，c的值为6，
∴5a+2b﹣c＝5×5+2×（﹣3）﹣6＝13，
∴5a+2b﹣c的平方根为．…………………………………………7分
19.解：（1）∵点P（2a﹣3，a+6）在x轴上，
∴a+6＝0，
解得：a＝﹣6，
∴2a﹣3＝2×（﹣6）﹣3＝﹣15，
∴点P的坐标（﹣15，0）；………………………………………………………2分
（2）∵点Q的坐标为（3，3），直线PQ∥y轴，
∴2a﹣3＝3，
解得：a＝3，
∴a+6＝3+6＝9，
∴点P的坐标为（3，9）；………………………………………………………5分
（3）∵点P在第二象限，且它到x轴、y轴的距离相等，
∴3﹣2a＝a+6，
解得：a＝﹣1，
∴a2023+2024＝（﹣1）2023+2024＝﹣1+2024＝2023．……………………………8分
20.(1)解：如图所示：△ABC即为所求；
…………………………………………………………2分
(2)解：如图所示：即为所求：
……………………………………………4分
由图可知：；………………………………………………5分
解：∵P为x轴上一点，、
∴，，
∴，…………………………………………………………………………………7分
∵，
∴P点的横坐标为：或；
∴或．…………………………………………………………………8分
21.解（1）∵点C在直线y＝2x的图象上，且点C的横坐标为2，
∴点C的坐标为（2，4），……………………………………………………………2分
把C（2，4）代入y＝﹣x+b得﹣2+b＝4，解得b＝6，
∴一次函数的解析式为y＝﹣x+6，…………………………………………………4分
把y＝0代入y＝﹣x+6得﹣x+6＝0，解得x＝6，
∴A点坐标为（6，0），
把x＝0代入y＝﹣x+6得y＝6，
∴B点坐标为（0，6），…………………………………………………………6分
∴AB＝…………………………………………………………8分
22.解：（1）设y甲＝k1x，
将坐标（4，80）代入，得
则4k1＝80，
∴k1＝20，
∴y甲＝20x，…………………………………………………………………3分
当x＝2时，y乙＝y甲＝20×2＝40，
设y乙＝k2x+b2，
将（0，20）和（2，40）分别代入，
解得，k2=10,b2=20，
∴y乙＝10x+20；…………………………………………………………………6分
（2）当x＝6时，
y甲+y乙＝20×6+10×6+20＝120+80＝200＞180，
即甲、乙两班植树的总量之和能超过180棵；………………………………8分
23.解：（1）的有理化因式是；的有理化因式是．
故答案为：；；……………………………………………………2分
（2）①；
②．………………………………4分
（3）
=
=……………………………………………………………………8分
24.(1)解：设函数关系式为：y=kx+b，代入A(1,3),B(0,2)得：
b=2,k=1
所以函数关系数为：y=x+2…………………………………………………………2分
(2)解：，
则
即，解得，
或；…………………………………………………………6分
（3）解：存在
①当时，点或；
②当时，可以得到；
③当时，设则有，
解得：，所以
综上所述：点或或或．……………10分