广东省惠州市惠阳区2021-2022学年六年级下学期数学期中试卷

这是一份广东省惠州市惠阳区2021-2022学年六年级下学期数学期中试卷，共14页。试卷主要包含了判断题，选择题，填空，计算，操作与实践，解决问题等内容，欢迎下载使用。

一、判断题（共5分）
1．若圆柱体积是圆锥的3倍，那么它们一定是等底等高。( ）
2．如果a× 38 =b× 23 ，则a：b=16：9。（ ）
3．比例尺就是一个前项是1的比，它的比值小于1。（ ）
4．右图中图形A绕点O旋转180°后就可以得到图形B。 （ ）
5．煤的总量一定，每天烧煤的数量与烧的天数成反比例。（ ）
二、选择题（共5分）
6．把一个圆柱削成一个与它等底等高的圆锥，圆锥的体积是削去部分的（ ）。
A．30%B．33%C．50%
7．将图形①绕点O逆时针旋转90°得到图形②的是（ ）。
A．B．C．
8．能与3：8组成比例的比是（ ）。
A．15：40B．0.6：0.24C．8：3
9．已知 B5 = 3A ，那么A和B（ ）。
A．成反比例B．成正比例C．不成比例
10．圆柱的底面半径和高都扩大到原米的2倍。它的体积扩大到原来的（ ）倍。
A．4B．6C．8
三、填空（共20分）
11．72： =15： 59 0.2：8=0.6：
12．如果2a=5b（a、b≠0），那么a：b= ： 。
13．时针从4时绕中心点顺时针旋转90°后是 时，从4时到5时时针旋转了 °。
14．等底等高的圆柱和圆锥的体积之和是16.72dm3，圆锥的体积是 dm3。
15．已知一个比例的两个内项互为倒数，其中一个外项是0.4，另一个外项是 。
16．一个圆锥和一个圆柱的底面积与体积分别相等，已知圆柱的高是18cm，圆锥的高是 cm。
17． 是（线段）比例尺，表示图上1cm相当于实际距离 ，转化成数值比例尺是 。如果AB两地相距560千米，地图上相距 厘米。
18．推门是 现象，缆车运动是 现象，剪中国结是 现象。（选填“平移”“旋转”或“轴对称”）
19．将体积为56.52dm3的铁块熔铸成一个底面半径为6dm的圆锥形零件，圆锥的高是 dm。
20．在比例尺是1：1000的平面图上，量的一个长方形广场的长是24cm，宽是18cm，这个长方形实际的周长是 m。
21．在括号里填写“正比例”、“反比例”或“不成比例”。
（1）长方形的长一定，长方形的面积和宽。
（2）人的身高和跳的高度。
（3）圆柱的侧面积一定，圆柱的底面周长和高。
四、计算（共23分）
22．直接写出得数
57 ÷ 38 = 49 + 23 = 2.8÷70%= 25×0.4×5=
6- 710 = 811 × 3332 = 3.14×52= 0.3×0.2÷0.3×0.2=
23．解方程
（1）43 ：x=0.75：1.8
（2）x： 87 = 72 ： 25
（3）x6 = 4.59
24．计算下面图形的表面积
25．计算下面图形的体积（单位：dm）
五、操作与实践（共17分）
26．按要求画图形
（1）以直线MN为对称轴作图形A的轴对称图形，得到图形B。
（2）将图形B绕点顺时针旋转90°得到图形C。
（3）将图形C向右平移8格，得到图形D。
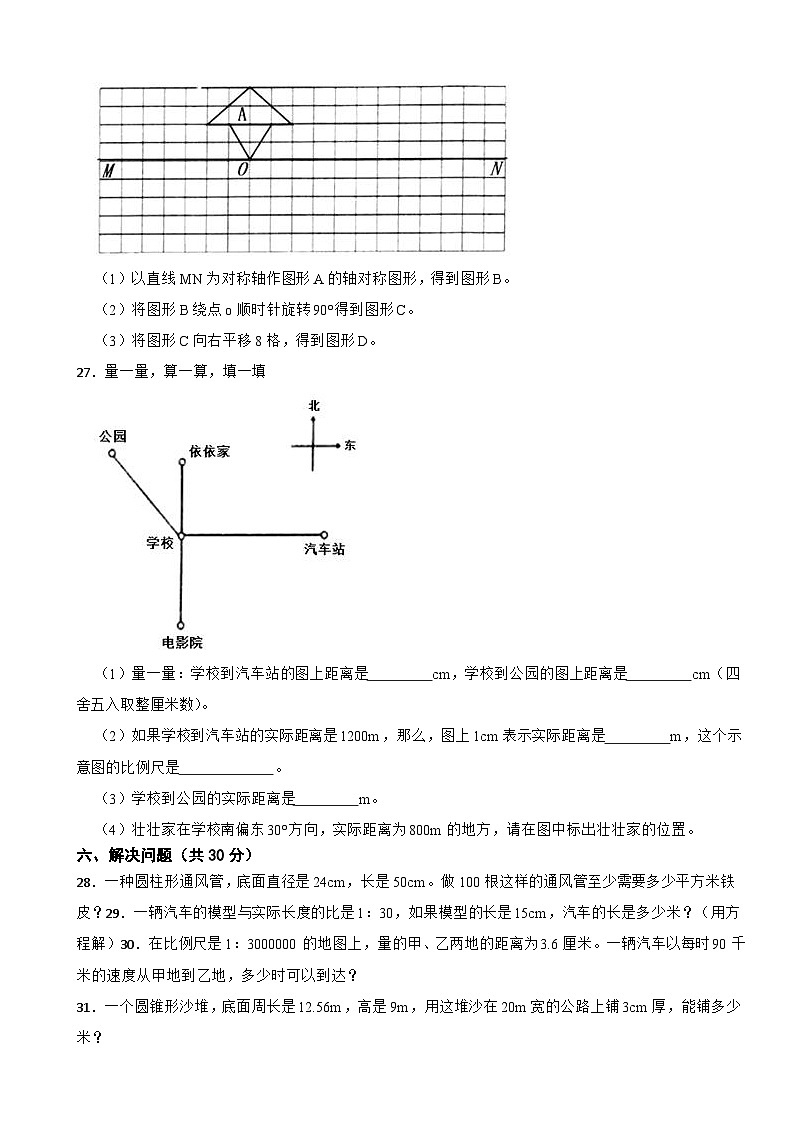
27．量一量，算一算，填一填
（1）量一量：学校到汽车站的图上距离是 cm，学校到公园的图上距离是 cm（四舍五入取整厘米数）。
（2）如果学校到汽车站的实际距离是1200m，那么，图上1cm表示实际距离是 m，这个示意图的比例尺是 。
（3）学校到公园的实际距离是 m。
（4）壮壮家在学校南偏东30°方向，实际距离为800m的地方，请在图中标出壮壮家的位置。
六、解决问题（共30分）
28．一种圆柱形通风管，底面直径是24cm，长是50cm。做100根这样的通风管至少需要多少平方米铁皮？29．一辆汽车的模型与实际长度的比是1：30，如果模型的长是15cm，汽车的长是多少米？（用方程解）30．在比例尺是1：3000000的地图上，量的甲、乙两地的距离为3.6厘米。一辆汽车以每时90千米的速度从甲地到乙地，多少时可以到达？
31．一个圆锥形沙堆，底面周长是12.56m，高是9m，用这堆沙在20m宽的公路上铺3cm厚，能铺多少米？
32．一个圆柱形水池，水池内壁和底面都要镶上瓷砖，水池底面直径6m，池深1.2m。
（1）镶瓷砖的面积是多少平方米？
（2）这个水池最多能装水多少升？
答案解析部分
1．【答案】（1）错误
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解：若圆柱体积是圆锥的3倍，那么它们不一定是等底等高。原题说法错误。
故答案为：错误。
【分析】等底等高的圆柱体积是圆锥体积的3倍，但是圆柱的体积是圆锥的3倍，它们不一定等底等高。
2．【答案】（1）正确
【知识点】比例的基本性质
【解析】【解答】解：a×38=b×23，所以a：b=23：38=16：9。
故答案为：正确。
【分析】在比例中，两个外项的积等于两个内项的积，据此作答即可。
3．【答案】（1）错误
【知识点】比例尺的认识
【解析】【解答】解：比例尺不一定是一个前项是1的比，它的比值也不一定小于1。
故答案为：错误。
【分析】比例尺=图上距离：实际距离，它的前项不一定是1，比值也不一定小于1。
4．【答案】（1）错误
【知识点】作旋转后的图形
【解析】【解答】解：图中图形A绕点O旋转180°后不能得到图形B。
故答案为：错误。
【分析】如图所示，图形A绕点O旋转180°后得到的B如下图所示。
5．【答案】（1）正确
【知识点】成反比例的量及其意义
【解析】【解答】解：煤的总量=每天烧煤的数量×烧的天数，所以煤的总量一定，每天烧煤的数量与烧的天数成反比例。
故答案为：正确。
【分析】若xy=k（k为常数，x，y≠0），那么x和y成反比例关系。
6．【答案】C
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解：圆锥的体积是削去部分的50%。
故答案为：C。
【分析】等底等高圆柱的体积是圆锥体积的3倍，所以削去的部分是圆锥体积的2倍，故圆锥的体积是削去部分的50%。
7．【答案】B
【知识点】作旋转后的图形
【解析】【解答】解：将图形①绕点O逆时针旋转90°得到图形②的是B项中的图形。
故答案为：B。
【分析】绕图形上一点逆时针旋转一定的度数，先把这个点连接的边逆时针旋转相同的度数，然后把剩下的边连接起来即可。
8．【答案】A
【知识点】比例的认识及组成比例的判断
【解析】【解答】解：3：8=38
A项中，15：40=38，所以能与3：8组成比例；
B项中，0.6：0.24=52，所以不能与3：8组成比例；
C项中，8：3=83，所以不能与3：8组成比例。
故答案为：A。
【分析】在比例中，能组成比例的两个比的比值要相等，据此作答即可。
9．【答案】A
【知识点】成反比例的量及其意义
【解析】【解答】解：B5=3A，所以AB=15，故A和B成反比例。
故答案为：A。
【分析】若xy=k（k为常数，x，y≠0），那么x和y成反比例关系。
10．【答案】C
【知识点】圆柱的体积（容积）
【解析】【解答】解：圆柱的底面半径和高都扩大到原米的2倍。它的体积扩大到原来的2×2×2=8倍。
故答案为：C。
【分析】圆柱的底面半径扩大几倍，体积就扩大几2倍；圆柱的高扩大几倍，体积就扩大几倍。
11．【答案】83；24
【知识点】比例的基本性质
【解析】【解答】解：72×59=40，40÷15=83，所以72：83=15：59；
8×0.6=4.8，4.8÷0.2=24，所以0.2：8=0.6：24。
故答案为：83；24。
【分析】在比例中，两个外项的积等于两个内项的积，据此作答即可。
12．【答案】5；2
【知识点】比例的基本性质
【解析】【解答】解：a：b=5：2。
故答案为：5；2。
【分析】在比例中，两个外项的积等于两个内项的积，据此作答即可。
13．【答案】7；30
【知识点】整点时间与钟面指针的指向
【解析】【解答】解：90°÷30°=3大格，4+3=7时，所以时针从4时绕中心点顺时针旋转90°后是7时；从4时到5时走了1大格，那么时针旋转了30°。
故答案为：7；30。
【分析】时针顺时针旋转90°，也就是走了90°÷30°=3大格，也就是走了3时，所以时针从4时绕中心点顺时针旋转90°后是7时；从4时到5时走了1大格，时针走1大格走了1时，那么时针旋转了30°。
14．【答案】4.18
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解：16.72÷（3+1）=4.18dm3，所以圆锥的体积是4.18m3。
故答案为：4.18。
【分析】等底等高圆柱的体积是圆锥体积的3倍，那么合起来是4倍圆锥的体积，所以圆锥的体积=圆柱和圆锥的体积和÷（3+1）。
15．【答案】2.5
【知识点】比例的基本性质
【解析】【解答】解：1÷0.4=2.5
故答案为：2.5。
【分析】两个内项互为倒数，两个内项的积是1，根据比例的基本性质可知，两个外项的积也是1；由此用1除以一个外项即可求出另一个外项。
16．【答案】54
【知识点】圆柱与圆锥体积的关系
【解析】【解答】解：18×3=54cm，所以圆锥的高是54cm。
故答案为：54。
【分析】V柱=S柱h柱，V锥=S锥h锥×13，当S柱=S锥，V柱=V锥时，h柱=h锥×13。
17．【答案】80km；1：8000000；7
【知识点】比例尺的认识；应用比例尺求图上距离或实际距离
【解析】【解答】解：线段比例尺表示图上1cm相当于实际距离80km；80km=8000000cm，所以转化成数值比例尺是1：8000000。如果AB两地相距560千米，560千米=56000000厘米，56000000×18000000=7厘米，所以地图上相距7厘米。
故答案为：80km；1：8000000；7。
【分析】比例尺=图上距离：实际距离，其中比例尺中的前项和后项的单位要一致；
AB两地的图上距离=AB两地的实际距离÷比例尺，这里需要把AB两地的实际距离的单位进行换算，即1千米=100000厘米。
18．【答案】旋转；平移；轴对称
【知识点】轴对称；平移与平移现象；旋转与旋转现象
【解析】【解答】解：推门是旋转现象，缆车运动是平移现象，剪中国结是轴对称现象。
故答案为：旋转；平移；轴对称。
【分析】旋转现象是图形或物体围绕某一点或轴进行圆周运动；
平移是指同一平面内，将一个图形上的所有点都按照某个直线方向做相同距离的移动；
轴对称是指平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形。
19．【答案】1.5
【知识点】圆锥的体积（容积）
【解析】【解答】解：56.52÷13÷（62×3.14）=169.56÷113.04=1.5dm，所以圆锥的高是1.5dm。
故答案为：1.5。
【分析】圆锥的高=铁块的体积÷13÷（圆锥的底面半径2×π），据此作答即可。
20．【答案】840
【知识点】应用比例尺求图上距离或实际距离
【解析】【解答】解：24÷11000=24000厘米=240米，18÷11000=18000厘米=180米，（240+180）×2=840米，所以这个长方形实际的周长是840m。
故答案为：840。
【分析】长方形实际的长=长方形图上的长÷比例尺，长方形实际的宽=长方形图上的宽÷比例尺，然后进行单位换算，即1米=100厘米，那么这个长方形实际的周长=（实际的长+实际的宽）×2。
21．【答案】（1）正比例
（2）不成比例
（3）反比例
【知识点】成正比例的量及其意义；成反比例的量及其意义
【解析】【解答】解：（1）长方形的面积=长×宽，所以长方形的长一定，长方形的面积和宽成正比例关系；
（2）人的身高和跳的高度不成比例；
（3）圆柱的侧面积=底面周长×高，所以圆柱的侧面积一定，圆柱的底面周长和高长反比例关系。
故答案为：（1）正比例；（2）不成比例；（3）反比例。
【分析】若y=kx（k为常数，x，y≠0），那么x和y成正比例关系；
若xy=k（k为常数，x，y≠0），那么x和y成反比例关系。
22．【答案】57 ÷ 38 = 4021 49 + 23 = 109 2.8÷70%=4 25×0.4×5=50
6- 710 = 5310 811 × 3332 = 34 3.14×52=78.5 0.3×0.2÷0.3×0.2=0.04
【知识点】小数的四则混合运算；分数与分数相乘；除数是分数的分数除法
【解析】【分析】除以一个不为0的数，等于乘这个数的倒数；
分数乘分数，用分子相乘的积做分子，分母相乘的积做分母，能约分的要约分。
23．【答案】（1）解： 0.75x=43×1.8
0.75x÷0.75=2.4÷0.75
x=3.2
（2）解： 25x=87×72
25x÷25=4÷25
x=10
（3）解：9x=4.5×6
9x÷9=27÷9
x=3
【知识点】应用比例的基本性质解比例
【解析】【分析】解比例时，可以用到比例的基本性质，即两个外项的积等于两个内项的积，把含有x的项放在等号的左边，把常数项放在等号的右边，然后等号两边同时除以x前面的项，就可以解得x的值。
24．【答案】解：12÷2=6（厘米）
62×3.14=113.04（平方厘米）
12×3.14×16
=37.68×16
=602.88（平方厘米）
602.88+113.04×2
=602.88+226.08
=828.96（平方厘米）
答：图形的表面积是828.96平方厘米。
【知识点】圆柱的侧面积、表面积
【解析】【分析】圆柱的底面半径=圆柱的底面直径÷2，所以圆柱的底面积=πr2，圆柱的侧面积=πdh，所以圆柱的表面积=底面积×2+侧面积。
25．【答案】解：4÷2=2（dm）
3.14×22=12.56（dm2）
V锥：12.56×3× 13 =12.56（dm3）
V柱：12.56×5=62.8（dm3）
62.8+12.56=75.36（dm3）
答：图形的体积是75.36dm3。
【知识点】圆柱的体积（容积）；圆锥的体积（容积）
【解析】【分析】从图中可以看出，这个图形的体积=圆柱的体积+圆锥的体积，其中圆柱的体积=πr2h，圆锥的体积=πr2h×13。
26．【答案】（1）
（2）
（3）
【知识点】补全轴对称图形；作平移后的图形；作旋转后的图形
【解析】【分析】（1）作轴对称图形，先过已知图形的关键点作对称轴的垂线，然后数出关键点到对称轴的格子数，并在对称轴另一边相同格子数的位置左上标记，最后把这些标记连接起来即可；
（2）绕图形上一点顺时针旋转一定的度数，先把这个点连接的边顺时针旋转相同的度数，然后把剩下的边连接起来即可；
（3）作平移后的图形，先把这个图形的关键点向右平移相同的格子数，然后把这些关键点连接起来即可。
27．【答案】（1）2；2
（2）600；1：60000
（3）1200
（4）解：
【知识点】根据方向和距离确定物体的位置；应用比例尺求图上距离或实际距离
【解析】【解答】解：（1）学校到汽车站的图上距离是2cm，学校到公园的图上距离是2cm；
（2）1200÷2=600m，所以图上1cm表示实际距离是600m；600m=60000cm，所以这个示意图的比例尺是1：60000；
（3）2÷160000=120000cm=1200m，所以学校到公园的实际距离是1200m；
（4）。
【分析】（1）用尺子两处长度，然后将长度取整即可；
（2）学校到汽车站的图上距离是2厘米，1200÷2=600m，所以图上1cm表示实际距离是1m；这个示意图的比例尺=图上距离：实际距离；
（3）学校到公园的实际距离=图上距离÷比例尺，然后进行单位换算；
（4）根据方位图和各个地点的位置作答即可。
28．【答案】解：24×50×3.14
=1200×3.14
=3768（平方厘米）
=0.3768（平方米）
0.3768×100=37.68（平方米）
答：做100根这样的通风管至少需要37.68平方米铁皮。
【知识点】圆柱的侧面积、表面积
【解析】【分析】1根这样的通风管需要铁皮的面积=铁皮管的底面直径×π×长，所以100根这样的通风管需要铁皮的面积=1根这样的通风管需要铁皮的面积×100，据此代入数值作答即可。
29．【答案】解：设汽车的长是x厘米。
1：30=15：x
x=30×15
x=450
450÷100=4.5（米）
答：汽车的长是4.5米。
【知识点】应用比例解决实际问题
【解析】【分析】本题可以设汽车的长是x厘米，题中存在的比例关系是：汽车的模型与实际长度的比=汽车模型的长：汽车实际的长，然后进行单位换算即可。
30．【答案】解：3.6÷ 13000000 =3.6×3000000=10800000（cm）
10800000cm=108km
108÷90=1.2（小时）
答：1.2小时可以到达。
【知识点】应用比例尺求图上距离或实际距离
【解析】【分析】甲乙两地的实际距离=甲乙两地的图上距离÷比例尺，然后进行单位换算，即1千米=100000厘米，那么这辆汽车从甲地到乙地用的时间=甲乙两地的实际距离÷这辆汽车的速度，据此代入数值作答即可。
31．【答案】解：12.56÷3.14÷2=2（米）
3.14×22×9×13=37.68（立方米）
3厘米=0.03米
37.68÷（0.03×20）=62.8（米）
答：能铺62.8米。
【知识点】长方体的体积；圆锥的体积（容积）
【解析】【分析】沙堆的底面半径=底面周长÷π÷2，所以沙堆的体积=πr2h×13，然后把单位统一，即1m=100cm，那么能铺的长度=沙堆的体积÷（公路的长×公路的宽），据此代入数值作答即可。
32．【答案】（1）解：6÷2=3（m）
①S侧：3.14×6×2×1.2=22.608（m2）
②S底：3.14×32=28.26（m2）
③S表：28.26+22.608=50.868（m2）
答：镶瓷砖的面积是50.868平方米。
（2）解：6÷2=3（m）
3.14×32×1.2=33.912（m3）
33.912m3=33912（升）
答：这个水池最多能装水33912升。
【知识点】圆柱的侧面积、表面积；圆柱的体积（容积）
【解析】【分析】（1）水池的底面半径=底面直径÷2，那么水池的侧面积=底面周长×π×高，水池的底面积=πr2，所以镶瓷砖的面积=侧面积+底面积；
（2）这个水池最多能装水的体积=πr2h，然后进行单位换算，即1m3=1000L。