吉林省长春市榆树市太安乡中学校2023-2024学年八年级上学期11月期中数学试题

这是一份吉林省长春市榆树市太安乡中学校2023-2024学年八年级上学期11月期中数学试题，共6页。

1．（3分）北京2022年冬奥会会徽“冬梦”已经发布．以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（ ）
A． B．C． D．
2．（3分）下列各组数可能是一个三角形的边长的是（ ）
A．1，2，4B．4，5，9C．4，6，8D．5，5，11
3．（3分）下列图形中具有稳定性的是（ ）
A．B．C．D．
4．（3分）如图，AC是△ABC和△ADC的公共边，下列条件中不能判定△ABC≌△ADC的是（ ）
A．∠1＝∠2，∠3＝∠4B．BC＝DC，∠3＝∠4
C．∠B＝∠D，∠1＝∠2D．AB＝AD，∠B＝∠D
5．（3分）点A（3，4）关于x轴的对称点的坐标是（ ）
A．（3，﹣4）B．（﹣3，4）C．（﹣3，﹣4）D．（﹣4，3）
6．（3分）从一个多边形的任何一个顶点出发都只有2条对角线，则它的边数是（ ）条．
A．3B．4C．5D．6
7．（3分）某城市几条道路的位置关系如图所示，道路AB∥CD，道路AB与AE的夹角∠BAE＝54°，城市规划部门想新修一条道路CE，要求使CF＝EF，则∠E的度数为（ ）
A．23°B．25°C．27°D．30°
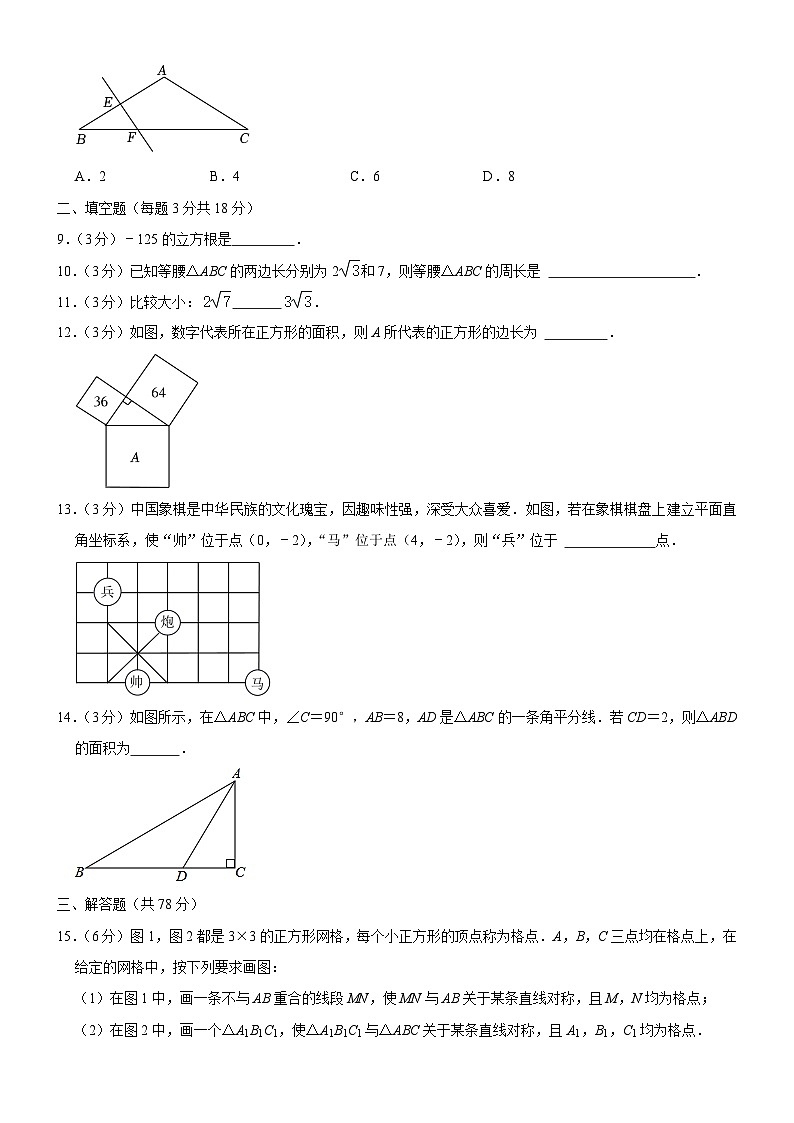
8．（3分）如图，在△ABC中，AB＝BC，∠BAC＝120°，AB的垂直平分线交AB于点E，交BC于点F，若BF＝2，则CF的长为（ ）
A．2B．4C．6D．8
二、填空题（每题3分共18分）
9．（3分）﹣125的立方根是 ．
10．（3分）已知等腰△ABC的两边长分别为2和7，则等腰△ABC的周长是 ．
11．（3分）比较大小： ．
12．（3分）如图，数字代表所在正方形的面积，则A所代表的正方形的边长为 ．
13．（3分）中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点（0，﹣2），“马”位于点（4，﹣2），则“兵”位于 点．
14．（3分）如图所示，在△ABC中，∠C＝90°，AB＝8，AD是△ABC的一条角平分线．若CD＝2，则△ABD的面积为 ．
三、解答题（共78分）
15．（6分）图1，图2都是3×3的正方形网格，每个小正方形的顶点称为格点．A，B，C三点均在格点上，在给定的网格中，按下列要求画图：
（1）在图1中，画一条不与AB重合的线段MN，使MN与AB关于某条直线对称，且M，N均为格点；
（2）在图2中，画一个△A1B1C1，使△A1B1C1与△ABC关于某条直线对称，且A1，B1，C1均为格点．
16．（6分）如图，点D在AB上，E在AC上，AB＝AC，∠B＝∠C，求证：AD＝AE．
17．（6分）计算
（1）（2b+2）2﹣（2b+2）（2b﹣2）
（2）（x+3）（x+4）﹣（x﹣1）2．
18．（6分）如图，∠A＝∠D，∠ACB＝∠DBC．求证：△ABC≌△DCB．
19．（6分）一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．
20．（6分）先化简，再求值：（a+1）（a﹣1）+a（3﹣a），其中a＝2．
21．（6分）如图，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，求∠DBC的度数．
22．（6分）用一条长为18cm细绳围成一个等腰三角形．
（1）如果腰长是底边的2倍，那么各边的长是多少？
（2）能围成有一边的长为4cm的等腰三角形吗？为什么？
23．（6分）如图，已知D为BC的中点，DE⊥AB，DF⊥AC，点E，F为垂足，且BE＝CF，∠BDE＝30°，求证：△ABC是等边三角形．
24．（6分）已知：如图，在Rt△ABC中，∠C＝90°，AD是△ABC的角平分线，DE⊥AB，垂足为点E，AE＝BE．
（1）求∠B的度数．
（2）如果AC＝3cm，CD＝2cm，求△ABD的面积．
25．（6分）如图，某小区有两个喷泉A，B，两个喷泉的距离长为250m．现要为喷泉铺设供水管道AM，BM，供水点M在小路AC上，供水点M到AB的距离MN的长为120m，BM的长为150m．
（1）求供水点M到喷泉A，B需要铺设的管道总长；
（2）求喷泉B到小路AC的最短距离．
26．（12分）如图，在平面直角坐标系中，直线l1：y＝kx+1交y轴于点A，交x轴于点B（4，0），过点E（2，0）的直线l2平行于y轴，交直线l1于点D，点P是直线l2上一动点（异于点D），连接PA、PB．
（1）直线l1的表达式为 ，点D的坐标为 ；
（2）设P（2，m），当点P在点D的下方时，求△ABP的面积S的表达式（用含m的代数式表示）；
（3）当△ABP的面积为3时，则以点B为直角顶点作等腰直角△BPC，请直接写出点C的坐标．
八年级数学答案
一．试题（共26小题，满分120分）
1． B．2． C．3． A．4． D．5． A．6． C．7． C．8． B．
9．
﹣5．
10．
14+2．
11．
＞．
12．
10．
13．
（﹣1，1）．
14．
8．
15．
16．
证明：在△ABE与△ACD中，
，
∴△ACD≌△ABE（ASA），
∴AD＝AE（全等三角形的对应边相等）．
17．
解：（1）（2b+2）2﹣（2b+2）（2b﹣2）
＝4b2+8b+4﹣4b2+4
＝8b+8；
（2）（x+3）（x+4）﹣（x﹣1）2
＝x2+4x+3x+12﹣x2+2x﹣1
＝9x+11．
18．
证明：在△ABC和△DCB中，
，
∴△ABC≌△DCB（AAS）．
19．
解：设这个正多边形的边数是n，
则（n﹣2）•180°＝1440°，
解得n＝10．
则从这个多边形一个顶点可以引7条对角线，
故这个多边形的对角线总条数为＝35条．
20．
解：原式＝a2﹣1+3a﹣a2
＝3a﹣1，
当a＝2时，原式＝3×2﹣1＝5．
21．
解：∵AB＝AC，
∴∠ABC＝∠ACB＝＝70°，
∵MN垂直平分AB，
∴DA＝DB，
∴∠A＝∠ABD＝40°，
∴∠DBC＝∠ABC﹣∠ABD＝70°﹣40°＝30°．
故答案为：30°．
22．
解：（1）设底边长为xcm，
∵腰长是底边的2倍，
∴腰长为2xcm，
∴2x+2x+x＝18，解得，x＝cm，
∴2x＝2×＝cm，
∴各边长为：cm，cm，cm．
（2）①当4cm为底时，腰长＝＝7cm；
②当4cm为腰时，底边＝18﹣4﹣4＝10cm，
∵4+4＜10，
∴不能构成三角形，故舍去；
∴能构成有一边长为4cm的等腰三角形，另两边长为7cm，7cm．
23．
证明：∵D是BC的中点，
∴BD＝CD，
∵DE⊥AB，DF⊥AC，
∴△BED和△CFD都是直角三角形，
在Rt△BED和Rt△CFD中，
，
∴Rt△BED≌Rt△CFD（HL），
∴∠B＝∠C，
∴AB＝AC（等角对等边）．
∵∠BDE＝30°，DE⊥AB，
∴∠B＝60°，
∴△ABC是等边三角形．
24．
解：（1）∵DE⊥AB且AE＝BE，
∴AD＝BD，
∴∠B＝∠DAE，
∵AD是△ABC的角平分线，
∴∠DAE＝∠DAC，
∴∠B＝∠DAE＝∠DAC，
∵∠C＝90°，
∴∠B+∠DAE+∠DAC＝90°，
∴∠B＝30°；
（2）∵∠C＝90°，AD是△ABC的角平分线，DE⊥AB，
∴CD＝ED，
在Rt△ACD与Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AE＝AC＝3cm，DE＝CD＝2cm，
∵AE＝BE，
∴AB＝2AE＝2×3＝6（cm），
∴S△ABD＝AB•DE＝×6×2＝6（cm2）．
25．
解：（1）在Rt△MNB中，BN＝＝＝90（m），
∴AN＝AB﹣BN＝250﹣90＝160（m），
在Rt△AMN中，AM＝＝＝200（m），
∴供水点M到喷泉A，B需要铺设的管道总长＝200+150＝350（m）；
（2）∵AB＝250m，AM＝200m，BM＝150m，
∴AB2＝BM2+AM2，
∴△ABM是直角三角形，
∴BM⊥AC，
∴喷泉B到小路AC的最短距离是BM＝150m．
26．
解：（1）∵直线l1：y＝kx+1交x轴于点B（4，0），
∴0＝4k+1．
∴k＝﹣．
∴直线l1：y＝﹣x+1，
把x＝2代入y＝﹣x+1得y＝，
∴点D的坐标为（2，），
故答案为：y＝﹣x+1；（2，）；
（2）由得：．
∴D（2，）．
∵P（2，m），
∴PD＝|m﹣|．
∴S＝×|4﹣0|•PD＝×|m﹣|×4＝|2m﹣1|．
当m＜时，S＝1﹣2m；
（3）当S△ABP＝3时，2m﹣1＝3，
解得m＝2，
∴点P（2，2），
∵E（2，0），
∴PE＝BE＝2，
∴∠EPB＝∠EBP＝45°，
如图2，∠PBC＝90°，BP＝BC，
过点C作CF⊥x轴于点F，
∵∠PBC＝90°，∠EBP＝45°，
∴∠CBF＝∠PBE＝45°，
在△CBF与△PBE中，
，
∴△CBF≌△PBE（AAS）．
∴BF＝CF＝PE＝EB＝2．
∴OF＝OB+BF＝4+2＝6．
∴C（6，2）；
如图3，△PBC是等腰直角三角形，
∴PE＝CE，
∴C（2，﹣2），
∴以点B为直角顶点作等腰直角△BPC，点C的坐标是（6，2）或（2，﹣2）．
当1﹣2m＝3时，m＝﹣1，可得P（2，﹣1），
同法可得C（3，2）或（5，﹣2）．
综上所述，满足条件的点C坐标为（6，2）或（2，﹣2）或（3，2）或（5，﹣2）．