吉林省长春市榆树市太安乡中学校2023-2024学年九年级上学期11月期中数学试题

这是一份吉林省长春市榆树市太安乡中学校2023-2024学年九年级上学期11月期中数学试题，共6页。

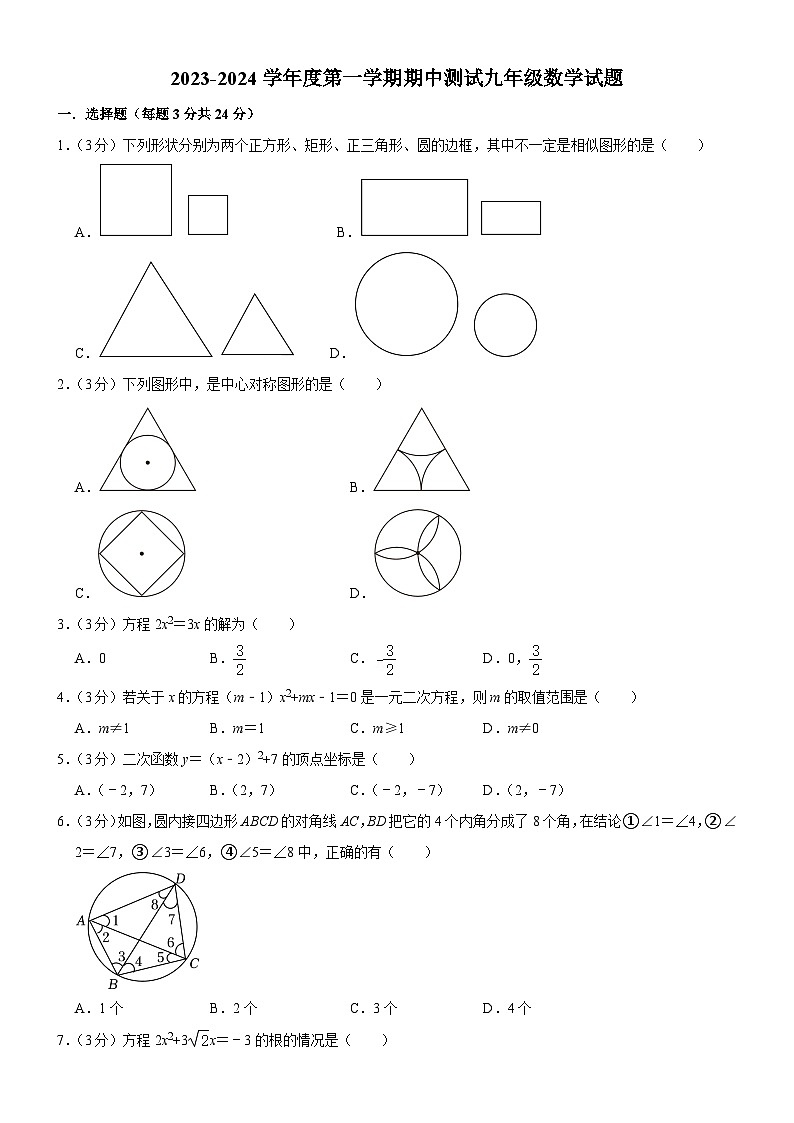
1．（3分）下列形状分别为两个正方形、矩形、正三角形、圆的边框，其中不一定是相似图形的是（ ）
A． B．
C． D．
2．（3分）下列图形中，是中心对称图形的是（ ）
A．B．
C．D．
3．（3分）方程2x2＝3x的解为（ ）
A．0B．C．D．0，
4．（3分）若关于x的方程（m﹣1）x2+mx﹣1＝0是一元二次方程，则m的取值范围是（ ）
A．m≠1B．m＝1C．m≥1D．m≠0
5．（3分）二次函数y＝（x﹣2）2+7的顶点坐标是（ ）
A．（﹣2，7）B．（2，7）C．（﹣2，﹣7）D．（2，﹣7）
6．（3分）如图，圆内接四边形ABCD的对角线AC，BD把它的4个内角分成了8个角，在结论①∠1＝∠4，②∠2＝∠7，③∠3＝∠6，④∠5＝∠8中，正确的有（ ）
A．1个B．2个C．3个D．4个
7．（3分）方程2x2+3x＝﹣3的根的情况是（ ）
A．只有一个实数根
B．有两个相等的实数根
C．有两个不相等的实数根
D．无实数根
8．（3分）如图，在长为100米，宽为80米的矩形场地上修建两条小路，剩余部分进行绿化，要使绿化面积为7644平方米，那么小路进出口的宽度应为多少米？设小路进出口的宽为x米，则可列方程为（注：所有小路进出口的宽度都相等，且每段小路均为平行四边形）（ ）
A．100×80﹣100x﹣80x＝7644
B．（100﹣x）（80﹣x）+x2＝7644
C．（100﹣x）（80﹣x）＝7644
D．（100﹣x）（80﹣x）﹣x2＝7644
二、填空题（每题3分共18分）
9．（3分）已知关于x的一元二次方程x2+5x﹣m＝0的一个根是2，则另一个根是 ．
10．（3分）若3m＝7n，则＝ ．
11．（3分）甲乙两人做游戏，同时掷两枚相同的硬币，双方约定：同面朝上甲胜，异面朝上则乙胜，则这个游戏 .（选填“公平”或“不公平”）
12．（3分）将函数y＝x2﹣2x+4化为y＝a（x﹣h）2+k的形式为 ．
13．（3分）如图，已知抛物线y＝﹣（x﹣h）2+k的对称轴为直线x＝1，且与x轴的一个交点的坐标为（3，0），那么它对应的函数解析式是 ．
14．（3分）如图，在Rt△ABC中，∠C＝90°，∠BAC＝40°，将Rt△ABC绕点A旋转得到Rt△AB'C'，且点C'落在AB上，则∠B'BC的度数为
三、解答题（共78分）
15．（5分）解方程：x2﹣4x﹣4＝0．（用配方法解答）
16．（5分）关于x的方程x2+2x+2k﹣1＝0有两个不相等的实数根，求k的取值范围．
17．（5分）已知抛物线的顶点坐标为（﹣1，﹣8），且过点（0，﹣6），求抛物线的解析式．
18．（5分）为增强学生身体素质，提高学生足球运动竞技水平，某市开展“希望杯”足球比赛，赛制为单循环形式（每两队之间赛一场）．现计划安排21场比赛，应邀请多少个球队参赛？
19．（6分）如图，在△ABC中，∠C＝90°，点D在AC上，DE⊥AB于点E．
（1）求证：△ADE∽△ABC；
（2）AC＝4，AB＝5且AD＝3，求AE的长．
​
20．（6分）如图，在平面直角坐标系中，△AOB的顶点A（﹣2，0）、B（﹣1，1），将△AOB绕点O顺时针旋转90°后，点A、B分别落在A′B′．
（1）在图中画出旋转后的△A′OB′；
（2）求点B旋转到点B′所经过的路线长．
21．（6分）百货商店服装柜在销售中发现：某品牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”国际儿童节，商场决定采取适当的降价措施，扩大销售量，增加盈利，减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，那么每件童装应降价多少元？
22．（5分）如图，⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD，BC．
求证：．
23．（6分）已知抛物线y＝﹣x2﹣2x﹣6．
（1）求此抛物线的对称轴；
（2）当﹣6＜x＜3时，直接写出y的取值范围．
24．（6分）飞机着陆后滑行的距离s（单位：m）关于滑行时间t（单位：s）的函数解析式是s＝60t﹣1.5t2．
（1）求飞机着陆后滑行多远才能停下来？
（2）下列图象能正确反映题中情景的是 （填序号）．
25．（5分）如图，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD．求证：△ABC∽△DEC．
26．（8分）如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（1，2），B（1，1），C（3，1），以原点O为位似中心，在坐标系内画△DEF，使它与△ABC位似，且相似比为2：1．
（1）画出△DEF；
（2）请直接写出△DEF的顶点坐标．
27．（10分）如图，在平面直角坐标系中，直线y1＝k1x+b与双曲线相交于A（﹣2，3），B（m，﹣2）两点，
（1）求y1，y2对应的函数表达式：
（2）根据函数图象，直接写出关于x的不等式k1x+b＜的解集．
（3）过点B作BP∥x轴交y轴于点P，在x轴上是否存在点Q，使得△ABQ的面积等于△ABP的面积的一半，若存在求出Q点的坐标．
九年级数学答案
1． B．2．C．3． D．4． A．5． B．6． D．7． D．8． C．
9．
﹣7．
10．
．
11．
公平．
12．
y＝（x﹣1）2+3．
13．
y＝﹣（x﹣1）2+4．
14．
120°
15．
解：∵x2﹣4x＝4，
∴x2﹣4x+4＝4+4，即（x﹣2）2＝8，
∴x﹣2＝±2，
则x＝2±2．
16．
解：∵关于x的方程x2+2x+2k﹣1＝0有两个不相等的实数根，
∴Δ＝22﹣4×1×（2k﹣1）＞0，
解得：k＜1，
∴k的取值范围为k＜1．
17．
解：由题意设函数的解析式是y＝a（x+1）2﹣8．
把（0，﹣6）代入函数解析式得a﹣8＝﹣6，
解得：a＝2，
则抛物线的解析式是y＝2（x+1）2﹣8．
18．
解：设：应该邀请x个球队参加，
由题意得：x（x﹣1）＝21，
解得：x＝7或x＝﹣6（舍去），
答：应邀请7个球队参赛．
19．
（1）证明：∵DE⊥AB于点E，∠C＝90°，
∴∠AED＝∠C＝90°，
∵∠A＝∠A，
∴△ADE∽△ABC；
（2）解：∵△ADE∽△ABC，
∴＝，
∵AC＝4，AB＝5，AD＝3，
∴＝，
∴AE＝．
20．
解：（1）如图所示：
（2）∵OB＝，
∴点B旋转到点B’所经过的路线长＝＝π．
21．
解：设每件童装应降价x元，根据题意列方程得，
（40﹣x）（20+2x）＝1200，
解得x1＝20，x2＝10（因为尽快减少库存，不合题意，舍去），
答：每件童装降价20元；
22．
证明：∵AB＝CD，
∴＝，
∴+＝+，
∴＝．
23．
解：（1）y＝﹣x2﹣2x﹣6，
对称轴直线x＝﹣＝＝﹣1；
（2）当x＝﹣1时，y＝﹣5，函数顶点坐标为：（﹣1，﹣5），
当x＝﹣6时，y＝﹣30，
故当﹣6＜x＜3时，y的取值范围为：﹣5≤y＜﹣30．
24．
解：（1）s＝60t﹣1.5t2
＝﹣1.5（t2﹣40t）
＝﹣1.5（ t2﹣40t+400﹣400）
＝﹣1.5（t﹣20）2+600．
∵﹣1.5＜0，
∴当t＝20时，飞机滑行的最远，最大值为600，
∴飞机着陆后滑行600米才能停下来；
（2）∵当s为最大值时，飞机停下来，
∴0≤t≤20，
故答案为：③．
25．
证明：∵∠BCE＝∠ACD，
∴∠DCE＝∠ACB，
又∵∠A＝∠D，
∴△ABC∽△DEC．
26．
解：（1）如图所示：△D′E′F′和△D″E″F″即为所求；
（2）D′（2，4），E′（2，2），F′（6，2），D″（﹣2，﹣4）E″（﹣2，﹣2），F″（﹣6，﹣2）．
27．
解：（1）∵直线y1＝k1x+b与双曲线相交于A（﹣2，3），B（m，﹣2）两点，
∴k2＝﹣2×3＝﹣2m，
∴k2＝﹣6，m＝3，
∴双曲线的表达式为：y2＝﹣，B（3，﹣2），
把A（﹣2，3）和B（3，﹣2）代入y1＝k1x+b得：，
解得：，
∴直线的表达式为：y1＝﹣x+1；
（2）观察图象，关于x的不等式k1x+b＜的解集为：﹣2＜x＜0或x＞3；
（3）过点A作AD⊥BP，交BP的延长线于点D，如图
∵BP∥x轴，
∴AD⊥x轴，BP⊥y轴，
∵A（﹣2，3），B（3，﹣2），
∴BP＝3，AD＝3﹣（﹣2）＝5，
∴S△ABP＝BP•AD＝＝，
∵△ABQ的面积等于△ABP的面积的一半，
∴S△ABQ＝，
设直线AB交x轴于C，则C（1，0），
∵S△ABQ＝S△ACQ+S△BCQ＝CQ•AD＝CQ，
∴CQ＝，
∴CQ＝，
∴Q（，0）或（﹣，0）．