吉林省长春市108中学2023-2024学年九年级上学期第三次月考数学试题

这是一份吉林省长春市108中学2023-2024学年九年级上学期第三次月考数学试题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8小题，每小题3分，共24分）
1．若为任意实数，则下列各式中是二次根式的是（ ）
A．B．C．D．
2．用配方法解方程，则配方正确的是（ ）
A．B．C．D．
3．如表，是某同学求代数式（为常数）的值的情况．根据表格中数据，可知方程的根是（ ）
A．B．C．D．
4．已知，则的值是（ ）
A．B．C．3D．
5．在和中，，若添加一个条件，使得，则下列条件中不符合要求的是（ ）
A．B．C．D．
6．如图，在数学兴趣小组探究活动中，小致要测量小河两岸相对的两点之间的距离，他和同学利用工具测得米，，根据上述测量数据可计算得到小河宽度为（ ）
（第6题）
A．米B．米C．米D．米
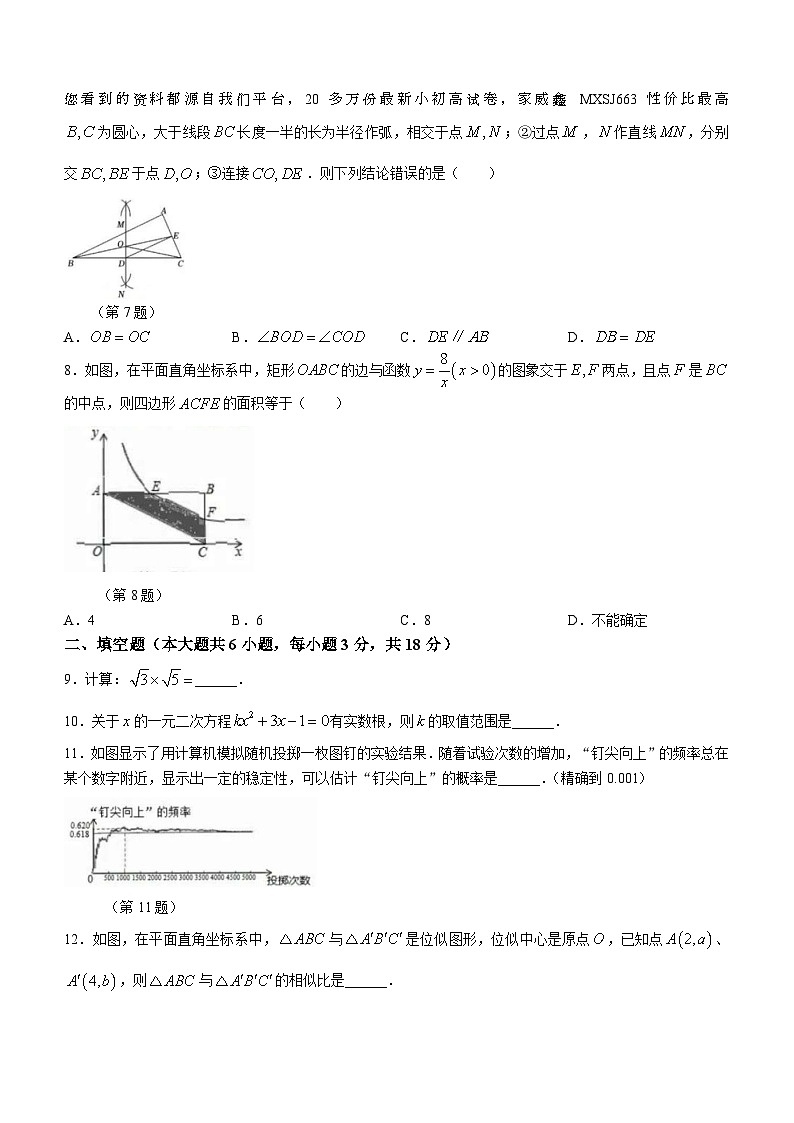
7．如图，已知在中，是边上的中线．按下列步骤作图：①分别以点您看到的资料都源自我们平台，20多万份最新小初高试卷，家威鑫 MXSJ663 性价比最高 为圆心，大于线段长度一半的长为半径作弧，相交于点；②过点，作直线，分别交于点；③连接．则下列结论错误的是（ ）
（第7题）
A．B．C．D．
8．如图，在平面直角坐标系中，矩形的边与函数的图象交于两点，且点是的中点，则四边形的面积等于（ ）
（第8题）
A．4B．6C．8D．不能确定
二、填空题（本大题共6小题，每小题3分，共18分）
9．计算：______．
10．关于的一元二次方程有实数根，则的取值范围是______．
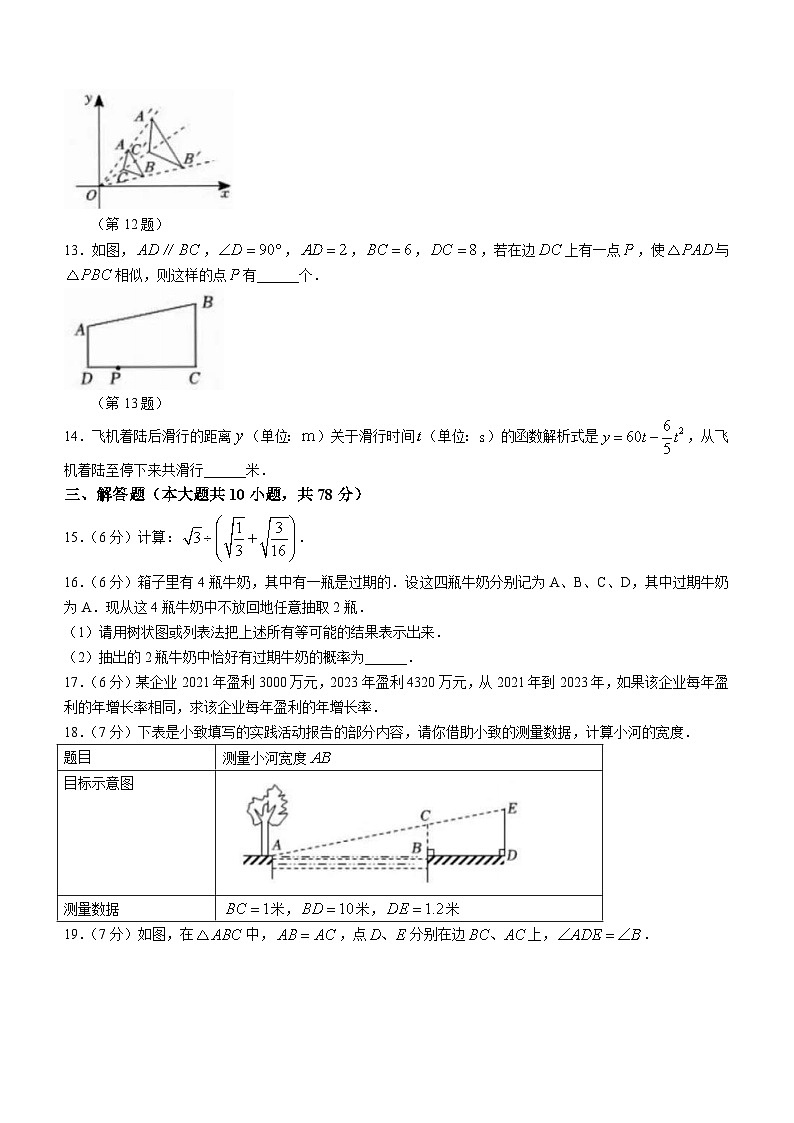
11．如图显示了用计算机模拟随机投掷一枚图钉的实验结果．随着试验次数的增加，“钉尖向上”的频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是______．（精确到0.001）
（第11题）
12．如图，在平面直角坐标系中，与是位似图形，位似中心是原点，已知点、，则与的相似比是______．
（第12题）
13．如图，，，，，，若在边上有一点，使与相似，则这样的点有______个．
（第13题）
14．飞机着陆后滑行的距离（单位：）关于滑行时间（单位：）的函数解析式是，从飞机着陆至停下来共滑行______米．
三、解答题（本大题共10小题，共78分）
15．（6分）计算：．
16．（6分）箱子里有4瓶牛奶，其中有一瓶是过期的．设这四瓶牛奶分别记为A、B、C、D，其中过期牛奶为A．现从这4瓶牛奶中不放回地任意抽取2瓶．
（1）请用树状图或列表法把上述所有等可能的结果表示出来．
（2）抽出的2瓶牛奶中恰好有过期牛奶的概率为______．
17．（6分）某企业2021年盈利3000万元，2023年盈利4320万元，从2021年到2023年，如果该企业每年盈利的年增长率相同，求该企业每年盈利的年增长率．
18．（7分）下表是小致填写的实践活动报告的部分内容，请你借助小致的测量数据，计算小河的宽度．
19．（7分）如图，在中，，点分别在边上，．
（第19题）
（1）求证：；
（2）若，则点到的距离为______．
20．如图是的小正方形构成的网格，每个小正方形的边长为1，的三个顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，不写画法，保留作图痕迹，画图过程用虚线表示，画图结果用实线表示．
图① 图② 图③
（第20题）
（1）在图①中，，作出的高，则______．
（2）在图②中，在边上找一点，使．
（3）在图③中，在内部找一点，使得．
21．（8分）观察下列算式，完成问题：
，验证：；
，验证：；
，验证：．
（1）按照上述三个等式及其验证过程的基本思路，猜想的变形结果并进行验证．
（2）针对上述各式反映的规律，请用含（，且为自然数）的等式表示出来．
22．（9分）问题背景：一次数学综合实践活动课上，小致发现并证明了关于三角形角平分线的一个结论．如图①，已知是的角平分线，可证．小致的证明思路是：如图②，过点作，交的延长线于点，构造相似三角形来证明．
图① 图② 图③ 图④
（第22题）
（1）尝试证明：请参照小致的思路，利用图②证明．
（2）基础训练：如图③，在中，是边上一点．连接，将沿所在直线折叠，点恰好落在边上的点处．若，则的长为______．
（3）拓展升华：如图④，中，平分的中垂线交延长线于点，当时，______．
23．（10分）如图，在中，，点为边的中点．点从点出发，以每秒2个单位长度的速度沿的方向匀速运动，回到点时停止运动，同时点从点出发，以每秒1个单位长度的速度沿向终点匀速运动．点不与点、重合．连接．设点的运动时间为．
（第23题）
（1）当点从点向点运动时，______；
当点从点向点运动时，______．（用含的代数式表示）
（2）当时，求的值．
（3）当与相似时，求的值．
（4）当点从点向点运动时，作点关于直线的对称点，点不与的顶点重合，连结，当与某一边垂直时，直接写出的值．
24．（12分）如图，在平面直角坐标系中，抛物线与轴交于点，与轴交于点，直线经过点．
（第24题）
（1）求抛物线的解析式．
（2）若点分别是抛物线上两点，若当时，，则的取值范围为______．
（3）点是抛物线上一个动点，当时，求点的坐标．
（4）若点为抛物线上的点，且点的横坐标为，已知点，，当点在四边形的内部时，直接写出的取值范围．
九年级数学学科参考答案
一、选择题（本大题共8小题，每小题3分，共24分）
1．C2．A3．A4．D
5．D6．D7．D8．B
二、填空题（本大题共6小题，每小题3分，共18分）
9．10．且．11．0.618．12．1:2．
13．2．14．750．
三、解答题（本大题共10小题，共78分）
15．原式．
16．（1）画树状图如图所示，
由图可知，共有12种等可能结果．
（2）．
17．解：设每年盈利的年增长率为，根据意，得
解得：（不合题意，舍去）
答：增长率为；
18．解：，，
则，即，
解得：，答：小河的宽度为50米．
19．（1）证明：，，
，
，；
（2）．
20．（1）如图①：即为所求；，
（2）如图2：点即为所求；
（3）如图3：点即为所求．
图① 图② 图③
21．解：（1）
验证：；
（2）．
验证：．
22．解：（1）证明：，，
，，
是的角平分线，，
又，，
，．
（2）
（3）3．
23．解：（1）；
（2）或
（3）如图②，
图② 图③
当时，则，
或
或6（舍弃）
如图③，当时，则，
或
或（舍弃）．
当到达终点后，，解得．
综上所述，的值为或或．
（4）
24．解：（1）当时，，，
当时，，，
将点代入，
，解得，
抛物线的解析式为；
（2）．
（3）当时，，
解得或，，
，
，
，是直角三角形，，
，，
当轴时，，此时；
在上截取，则，
点在直线上，
在中，，
，解得，，
设直线的解析式为，，
解得，直线的解析式为，
当时，解得或，
；
综上所述：点坐标为或．
（4）或．0
1
2
3
6
2
0
0
2
6
题目
测量小河宽度
目标示意图
测量数据
米，米，米