清北教育高考数学二轮专题精讲教师版

这是一份清北教育高考数学二轮专题精讲教师版，共506页。试卷主要包含了数集的基本运算，点集的基本运算，元素的互异性，子集的个数，韦恩图的运用，集合中的参数问题等内容，欢迎下载使用。
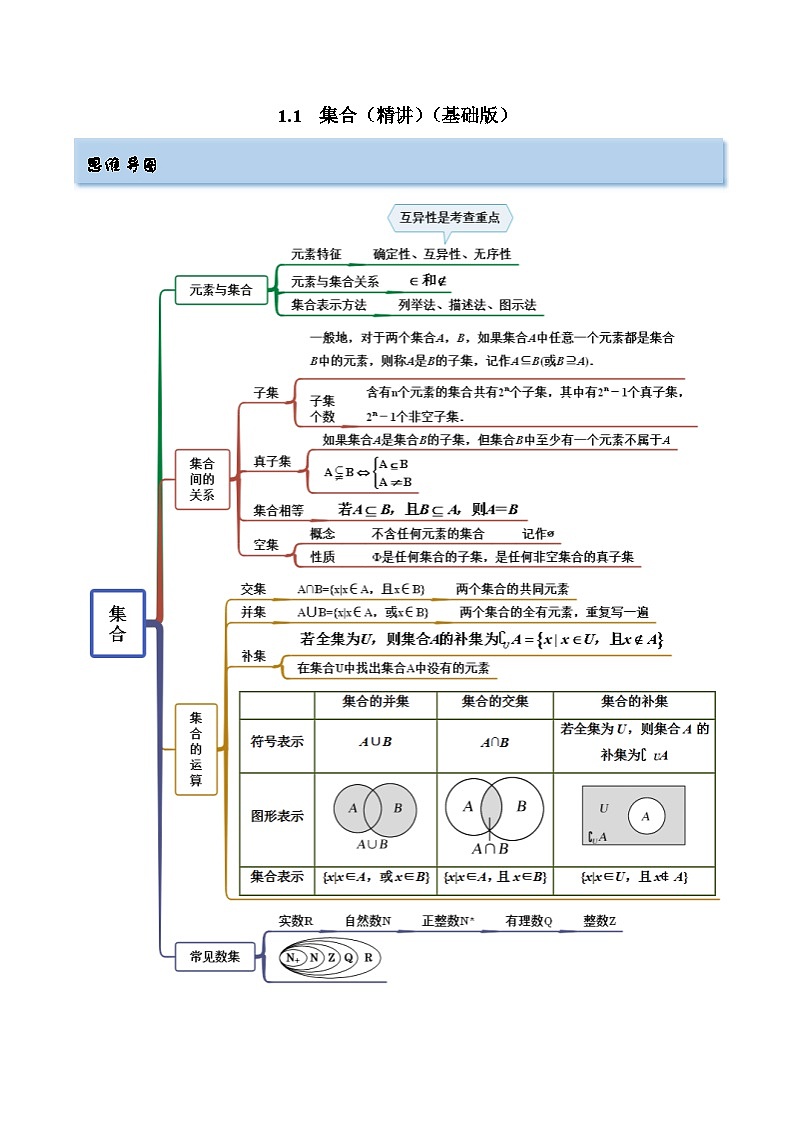
1.1 集合（精讲）（基础版）
思维导图


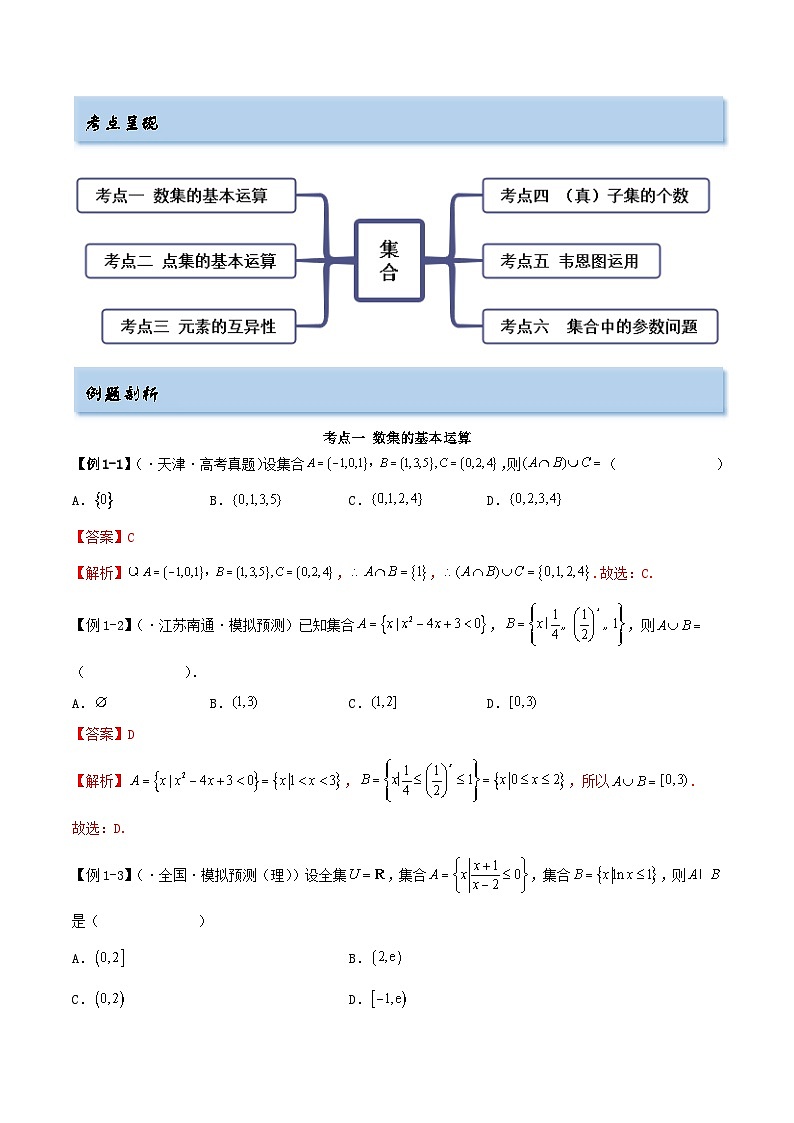
考点呈现



例题剖析

考点一 数集的基本运算
【例1-1】（·天津·高考真题）设集合，则（       ）
A． B． C． D．
【答案】C
【解析】，，.故选：C.
【例1-2】（·江苏南通·模拟预测）已知集合，，则（       ）．
A． B． C． D．
【答案】D
【解析】，，所以.
故选：D.
【例1-3】（·全国·模拟预测（理））设全集，集合，集合，则是（       ）
A． B．
C． D．
【答案】C
【解析】，解得：，故集合，，解得：，集合，则，故选：C．

1. 离散型数集或抽象集合间的运算,常借用Venn图或观察法求解
2. 集合中的元素若是连续的实数（常见为不等式）,常借助数轴求解,但要注意端点值能否取到
3. 解指数对数不等式时，一般把数字变成跟题目同底数的指数对数，再利用单调性解不等式。
4. 易错点：对数的真数部分恒大于0
方法总结

【一隅三反】
1．（·湖南·高考真题）已知集合，，且（       ）
A． B．
C． D．
【答案】A
【解析】因为集合，所以，故选：A.
2．（·江西·临川一中）已知集合，，则（       ）
A． B． C． D．
【答案】B
【解析】∵集合，，
∴.故选：B.
3．（·黑龙江·齐齐哈尔市）设集合，则（       ）
A． B． C． D．
【答案】D
【解析】由，得，由，解得：，所以，所以，故选：D.
考点二 点集的基本运算
【例2-1】（·上海·高三阶段练习）已知集合，，则(       )
A． B． C． D．
【答案】D
【解析】，∴{(－2，1)}.故选：D.
【例2-2】（·河南省直辖县级单位）已知集合，，则（       ）
A． B． C．M D．N
【答案】D
【解析】，
因为当时，，所以函数过点，所以，所以.
故选：D.

如果集合的元素是点集时，两个集合的交集即为两个方程的交点，一般采用联立方程或几何法解题




温馨提示

【一隅三反】
1．（·辽宁）已知集合，，则（ ）
A． B． C． D．
【答案】A
【解析】解得，或，．故选：A．
2（·全国·高三专题练习）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为实数，且x+y=1}，则A∩B的元素个数为（ ）
A．4 B．3 C．2 D．1
【答案】C
【解析】由题得∴或A∩B={(1,0),(0,1)}.故选C.
3．（·浙江·模拟预测）已知集合，，则（       ）
A． B． C． D．
【答案】C
【解析】的反函数为：
联立与得：，解得：，代入中，解得：，故交点坐标为，所以故选：C
考点三 元素的互异性
【例3-1】（·浙江·高三专题练习）已知，，若集合，则的值为（       ）
A． B． C． D．
【答案】B
【解析】因为，所以，解得或，
当时，不满足集合元素的互异性，故，，，故选：B.
【例3-2】（·甘肃）若以集合的四个元素为边长构成一个四边形，则这个四边形可能是（  ）
A．矩形 B．平行四边形
C．梯形 D．菱形
【答案】C
【解析】由题意，集合的四个元素为边长构成一个四边形，根据集合中元素的互异性，可得四个元素互不相等，以四个元素为边长构成一个四边形，结合选项，只能为梯形.故选：C.
【一隅三反】
1．（·浙江·高三专题练习）由实数所组成的集合，最多可含有（       ）个元素
A．2 B．3 C．4 D．5
【答案】B
【解析】由题意，当时所含元素最多，此时分别可化为，，，
所以由实数所组成的集合，最多可含有3个元素．故选：B
2（·上海市上南中学高三阶段练习）若集合中三个元素为边可构成一个三角形，那么该三角形一定不可能是（       ）
A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形
【答案】D
【解析】由集合中元素的互异性可知，这个三角形的三边必须都不相同，因此不可能为等腰三角形.
故选：D.
3.（·上海民办南模中学高三阶段练习）若，则实数a的取值集合为______．
【答案】
【解析】因为，故或或，
当时，，与元素的互异性矛盾，舍；
当时，，符合；
当时，或，根据元素的互异性，符合，
故a的取值集合为.故答案为：
考点四 （真）子集的个数
【例4】（·全国·模拟预测）已知集合，，则集合B的子集的个数是（       ）
A．3 B．4 C．8 D．16
【答案】C
【解析】依题意，所以集合B的子集的个数为，故选：C.
【一隅三反】
1（·新疆喀什）设集合，则集合的元素个数为（       ）
A．0 B．1 C．2 D．3
【答案】B
【解析】集合，所以.故选：B.
2（·重庆实验外国语学校一模）已知集合，则集合的所有非空子集的个数为（       ）
A．5个 B．6个 C．7个 D．8个
【答案】C
【解析】由题设，，即8可被整除且，，
∴，故集合的所有非空子集的个数为.故选：C
3．（·福建·模拟预测）设集合， ，则集合元素的个数为（       ）
A．2 B．3 C．4 D．5
【答案】B
【解析】当时，y＝1；当时，y＝0；当x＝3时，．故集合B共有3个元素．选：B.
考点五 韦恩图的运用
【例5-1】（·广东茂名·高三阶段练习）已知全集，集合，，则图中阴影部分所表示的集合为（       ）

A． B． C． D．
【答案】A
【解析】因为，，所以，由韦恩图可知阴影部分表示；故选：A
【例5-2】（·安徽·合肥一中）设集合U=R， ，，则图中阴影部分表示的集合为（       ）

A．{x|x≥1} B．{x|1≤x1，或x