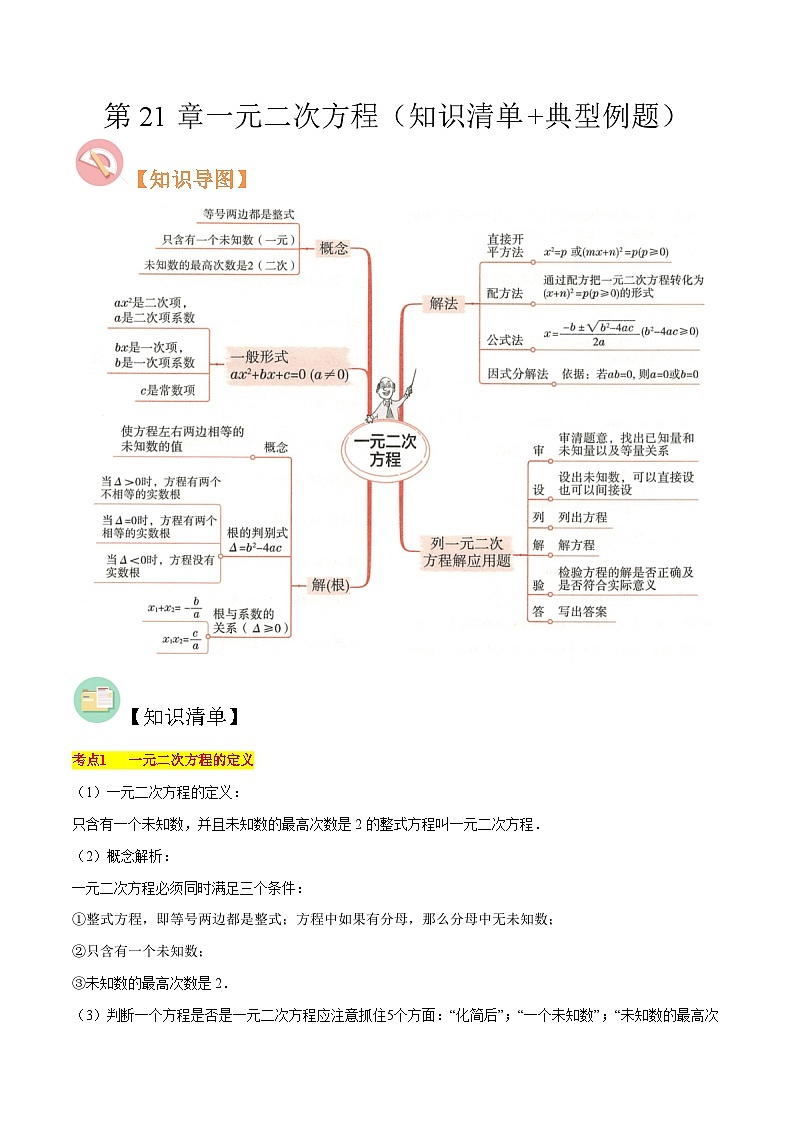
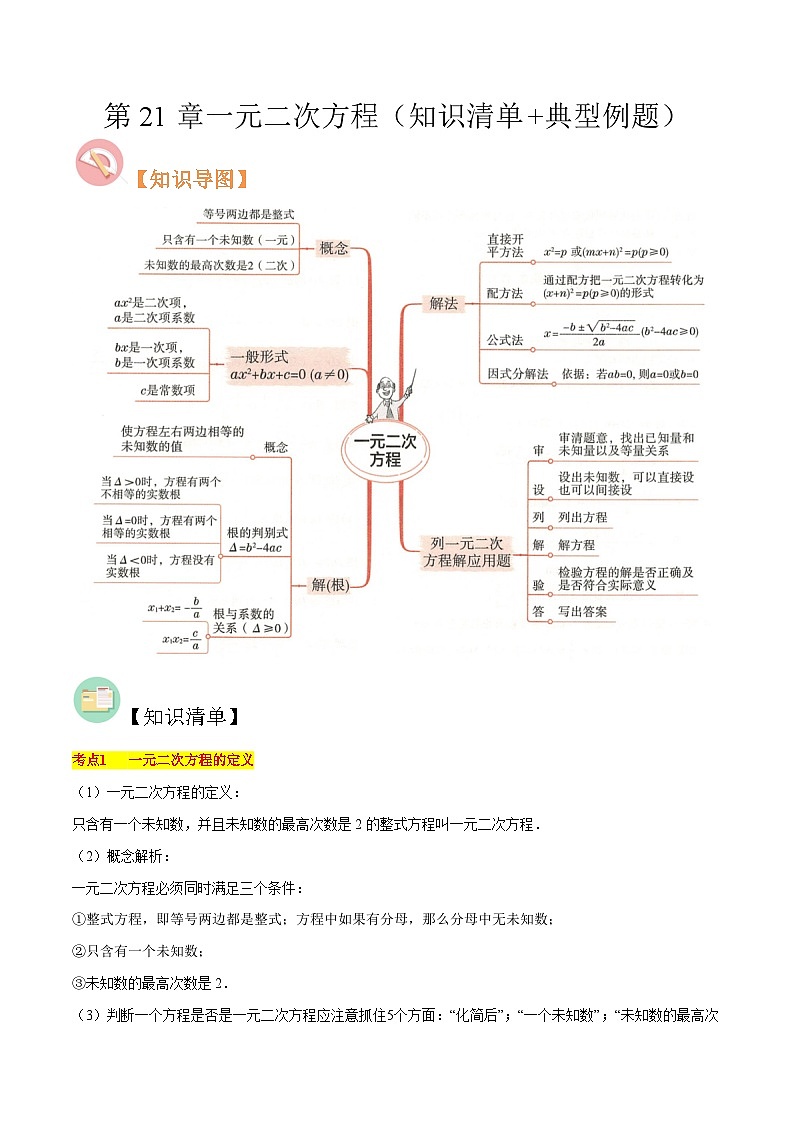
第21章 一元二次方程（知识清单+典型例题）-2023-2024学年九年级数学上学期期中考点大串讲（人教版）

这是一份第21章 一元二次方程（知识清单+典型例题）-2023-2024学年九年级数学上学期期中考点大串讲（人教版），共4页。


【知识清单】
一元二次方程的定义
（1）一元二次方程的定义：
只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程．
（2）概念解析：
一元二次方程必须同时满足三个条件：
①整式方程，即等号两边都是整式；方程中如果有分母，那么分母中无未知数；
②只含有一个未知数；
③未知数的最高次数是2．
判断一个方程是否是一元二次方程应注意抓住5个方面：“化简后”；“一个未知数”；“未知数的最高次数是2”；“二次项的系数不等于0”；“整式方程”．
【例1】（2022秋•镇江期末）下列方程中，一定是一元二次方程的是（ ）
A．B．x2+2x+3＝x（x+1）
C．2x+3y＝6D．x2﹣2x+3＝0
【分析】根据一元二次方程的定义逐个判断即可．
【解答】解：A．此方程是分式方程，不是整式方程，不是一元二次方程，故本选项不符合题意；
B．由原方程变形得到：x+3＝0，该方程是关于x的一元一次方程，故本选项不符合题意；
C．方程2x+3y＝6中含有两个未知数，不是一元二次方程，故本选项不符合题意；
D．方程x2﹣2x+3＝0是一元二次方程，故本选项符合题意；
故选：D．
【点评】本题考查了一元二次方程的定义，能熟记一元二次方程的定义是解此题的关键，只有一个未知数，并且所含未知数的项的最高次数是2的整式方程，叫一元二次方程．
【变式】（2023•大连一模）若方程kx2﹣2x+1＝0是关于x的一元二次方程，则k的取值范围是（ ）
A．k＞0B．k≠0C．k＜0D．k为实数
【分析】根据是一元二次方程的条件：二次项系数不为0，即可确定k的取值范围．
【解答】解：根据题意得：k≠0．
故选：B．
【点评】本题考查了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c＝0（a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．
一元二次方程的一般形式
（1）一般地，任何一个关于x的一元二次方程经过整理，都能化成如下形式ax2+bx+c=0（a≠0）．这种形式叫一元二次方程的一般形式．
其中ax2叫做二次项，a叫做二次项系数；bx叫做一次项；c叫做常数项．一次项系数b和常数项c可取任意实数，二次项系数a是不等于0的实数，这是因为当a=0时，方程中就没有二次项了，所以，此方程就不是一元二次方程了．
要确定二次项系数，一次项系数和常数项，必须先把一元二次方程化成一般形式．
【例2】（2022秋•新会区期末）把方程x（x+1）＝3（x﹣2）化成一般式ax2+bx+c＝0（a＞0）的形式，则a、b、c的值分别是（ ）
A．a＝1，b＝﹣2，c＝﹣3B．a＝1，b＝﹣2，c＝﹣6
C．a＝1，b＝﹣2，c＝3D．a＝1，b＝﹣2，c＝6
【分析】先去括号，再移项、合并同类项，化为ax2+bx+c＝0（a＞0）的形式，再根据对应相等得到a、b、c的值．
【解答】解：去括号得，x2+x＝3x﹣6，
移项得，x2﹣2x+6＝0，
所以a、b、c的值可以分别是1，﹣2，6．
故选：D．
【点评】一元二次方程的一般形式为ax2+bx+c＝0（a≠0，a，b，c为常数），其中a叫二次项系数，b叫一次项系数，c叫常数项．
一元二次方程的解
（1）一元二次方程的解（根）的意义：
能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．
（2）一元二次方程一定有两个解，但不一定有两个实数解．这x1，x2是一元二次方程ax 2+bx+c=0（a≠0）的两实数根，则下列两等式成立，并可利用这两个等式求解未知量．
ax12+bx1+c=0（a≠0），ax22+bx2+c=0（a≠0）．
【例3】（2023•陇西县校级模拟）若x＝1是关于x的一元二次方程x2+ax+2b＝0的解，则3a+6b＝（ ）
A．﹣1B．﹣2C．﹣3D．﹣6
【分析】把x＝1代入一元二次方程得到a+2b＝﹣1，再把3a+6b变形为3（a+2b），然后利用整体代入的方法计算．
【解答】解：把x＝1代入方程x2+ax+2b＝0得1+a+2b＝0，
所以a+2b＝﹣1，
所以3a+6b＝3（a+2b）＝3×（﹣1）＝﹣3．
故选：C．
【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
解一元二次方程-直接开平方
形如x2=p或（nx+m）2=p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．
如果方程化成x2=p的形式，那么可得x=±；
如果方程能化成（nx+m）2=p（p≥0）的形式，那么nx+m=±．
注意：①等号左边是一个数的平方的形式而等号右边是一个非负数．
②降次的实质是由一个二次方程转化为两个一元一次方程．
③方法是根据平方根的意义开平方．
【例4】（2022秋•南关区校级期末）解方程：2（x﹣3）2＝8．
【分析】先把方程变形得到（x﹣3）2＝4，再把方程两边开方得到x﹣3＝±2，然后解一次方程即可．
【解答】解：2（x﹣3）2＝8，
（x﹣3）2＝4，
x﹣3＝±2，
所以x1＝5，x2＝1．
【点评】本题考查了解一元二次方程﹣直接开平方法：形如x2＝p或（nx+m）2＝p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．
解一元二次方程-配方法
（1）将一元二次方程配成（x+m）2=n的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法．
（2）用配方法解一元二次方程的步骤：
①把原方程化为ax2+bx+c=0（a≠0）的形式；
②方程两边同除以二次项系数，使二次项系数为1，并把常数项移到方程右边；
③方程两边同时加上一次项系数一半的平方；
④把左边配成一个完全平方式，右边化为一个常数；
⑤如果右边是非负数，就可以进一步通过直接开平方法来求出它的解，如果右边是一个负数，则判定此方程无实数解．
【例5】（2023春•通州区期末）解方程：x2﹣4x﹣2＝0．
【解答】解：x2﹣4x﹣2＝0，
移项得：x2﹣4x＝2，
配方得：x2﹣4x+4＝2+4，
即（x﹣2）2＝6，
开方得：x﹣2＝±，
∴原方程的解是：x1＝2+，x2＝2﹣．
【变式】如何用配方法解方程
解：移常数项
方程两边同除以二次项系数
两边配上一次项系数一半的平方
转化为的形式
开平方
解得求解
所以原方程的根是.
解一元二次方程-公式法
（1）把（b2﹣4ac≥0）叫做一元二次方程ax2+bx+c=0（a≠0）的求根公式．
（2）用求根公式解一元二次方程的方法是公式法．
（3）用公式法解一元二次方程的一般步骤为：
①把方程化成一般形式，进而确定a，b，c的值（注意符号）；
②求出b2﹣4ac的值（若b2﹣4ac＜0，方程无实数根）；
③在b2﹣4ac≥0的前提下，把a、b、c的值代入公式进行计算求出方程的根．
注意：用公式法解一元二次方程的前提条件有两个：①a≠0；②b2﹣4ac≥0．
【例6】（2023•博山区二模）用公式法解方程：x2+2x﹣1＝0．
∵a＝1，b＝2，c＝﹣1，
∴b2﹣4ac＝22﹣4×1×（﹣1）＝8＞0，
∴，
∴，．
解一元二次方程-因式分解
（1）因式分解法解一元二次方程的意义
因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
因式分解法就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
（2）因式分解法解一元二次方程的一般步骤：
①移项，使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零，得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解．
【例7】（2023春•泰安期中）用因式分解法解方程：3x（x﹣2）＝2x﹣4．
【解答】解：方程整理得：3x（x﹣2）﹣2（x﹣2）＝0，
分解因式得：（x﹣2）（3x﹣2）＝0，
所以x﹣2＝0或3x﹣2＝0，
解得：x1＝2，x2＝．
【变式1】解关于的一元二次方程：．
【答案】．
【解析】移项，得：，
，
，
，
，
解得：．
【变式2】解下列一元二次方程：(2x+1)2+4(2x+1)+4＝0；
【答案与解析】(2x+1)2+4(2x+1)+4＝0，
(2x+1+2)2＝0．即，
∴．
【变式3】用合适的方法解下列关于的方程：
（1）；（2）；
【答案】（1）；（2）；
【解析】（1），
，
解得：；
（2）
，
解得：；
考点8 一元二次方程根的判别式及根与系数的关系
1.一元二次方程根的判别式
一元二次方程中，叫做一元二次方程的根的判别式，通常用“”来表示，即.
（1）当△>0时，一元二次方程有2个不相等的实数根；
（2）当△=0时，一元二次方程有2个相等的实数根；
（3）当△<0时，一元二次方程没有实数根.
【例8】（2023•扎兰屯市一模）已知a、b、c是△ABC的三条边的长，那么方程的根的情况是（ ）
A．没有实数根B．有两个相等的实数根
C．有两个不相等的负实根D．有两个不相等的正实根
【分析】判断上述方程的根的情况，只要看根的判别式Δ＝b2﹣4ac的值的符号，结合三角形三边关系即可作出判断．
【解答】解：在此方程中Δ＝b2﹣4ac＝（a+b）2﹣4c×＝（a+b）2﹣c2，
∵a，b，c是△ABC三条边的长，
∴a＞0，b＞0，c＞0．c＜a+b，即（a+b）2＞c2，
∴Δ＝（a+b）2﹣c2＞0，
故方程有两个不相等的实数根，
又∵两根的和是﹣＜0，两根的积是＞0，
∴方程cx2+（a+b）x+＝0的根的情况是有两个不相等的负根．
故选：C．
【点评】此题考查了根与系数的关系和根的判别式，一元二次方程根的情况与判别式△的关系：
（1）Δ＞0⇔方程有两个不相等的实数根；
（2）Δ＝0⇔方程有两个相等的实数根；
（3）Δ＜0⇔方程没有实数根．
三角形三边关系：两边之和大于第三边，两边之差小于第三边
2.一元二次方程的根与系数的关系
如果一元二次方程的两个实数根是，
那么，.
注意它的使用条件为a≠0， Δ≥0.
要点诠释：
1.一元二次方程的根的判别式正反都成立．利用其可以解决以下问题：
(1)不解方程判定方程根的情况；
(2)根据参系数的性质确定根的范围；
(3)解与根有关的证明题．
2. 一元二次方程根与系数的应用很多：
(1)已知方程的一根，不解方程求另一根及参数系数；
(2)已知方程，求含有两根对称式的代数式的值及有关未知数系数；
(3)已知方程两根，求作以方程两根或其代数式为根的一元二次方程．
【例9】（2023•迎江区校级三模）已知x1，x2是方程5x2+2x＝x+5的两个实数根，计算x1﹣x1x2+x2值得（ ）
A．B．1C．D．
【分析】根据根与系数的关系可得出，再整体代入，即可得出结论．
【解答】解：方程5x2+2x＝x+5整理得5x2+x﹣5＝0，
∵x1，x2是方程5x2+2x＝x+5的两个实数根，
∴，
∴．
故选：C．
【点评】此题考查一元二次方程根与系数的关系：x1，x2是方程ax2+bx+c＝0（a≠0）的两个实数根，则，，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
考点9 一元二次方程的应用
1、列方程解决实际问题的一般步骤是：审清题意设未知数，列出方程，解所列方程求所列方程的解，检验和作答．
2、列一元二次方程解应用题中常见问题：
1.数字问题
(1)任何一个多位数都是由数位和数位上的数组成.数位从右至左依次分别是：个位、十位、百位、千位……，它们数位上的单位从右至左依次分别为：1、10、100、1000、……，数位上的数字只能是0、1、2、……、9之中的数，而最高位上的数不能为0.因此，任何一个多位数，都可用其各数位上的数字与其数位上的单位的积的和来表示，这也就是用多项式的形式表示了一个多位数.如：一个三位数，个位上数为a，十位上数为b，百位上数为c，则这个三位数可表示为： 100c+10b+a.
(2)几个连续整数中，相邻两个整数相差1.
如：三个连续整数，设中间一个数为x，则另两个数分别为x-1，x+1.
几个连续偶数(或奇数)中，相邻两个偶数(或奇数)相差2.
如：三个连续偶数(奇数)，设中间一个数为x，则另两个数分别为x-2，x+2.
【例10】（2022秋·广西钦州·九年级统考期中）两个相邻偶数，的积是，这两个偶数的和为．
【答案】
【分析】根据题意，设，根据题意列出一元二次方程即可求解．
【详解】解：依题意，设，则，
解得：，则，
∵
∴
故答案为：．
【点睛】本题考查了一元二次方程的应用，根据题意列出一元二次方程是解题的关键．
2.平均变化率问题
列一元二次方程解决增长(降低)率问题时，要理清原来数、后来数、增长率或降低率，以及增长或降低的次数之间的数量关系.如果列出的方程是一元二次方程，那么应在原数的基础上增长或降低两次.
(1)增长率问题：
平均增长率公式为 (a为原来数，x为平均增长率，n为增长次数，b为增长后的量.)
降低率问题：
平均降低率公式为 (a为原来数，x为平均降低率，n为降低次数，b为降低后的量.)
【例11】（2023·福建泉州·统考模拟预测）年某电影上映的第一天票房为亿元，第二天、第三天单日票房持续增长，三天累计票房为亿元，若第二天、第三天单日票房按相同的增长率增长，设平均每天票房的增长率为，则根据题意，下列方程正确的是（ ）
A．B．
C．D．
【答案】D
【分析】根据第一天的票房及平均每天票房的增长率，可得出该电影上映的第二天票房为亿元，第三天票房为亿元，结合三天累计票房为亿元，即可得出关于的一元二次方程，此题得解．
【详解】解：某电影上映的第一天票房为亿元，且平均每天票房的增长率为，
该电影上映的第二天票房为亿元，第三天票房为亿元，
根据题意得，
故选：D．
【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
3、比赛问题：解决此类问题的关键是分清单循环和双循环 ．
4、传播问题：
，a表示传染前的人数，x表示每轮每人传染的人数，n表示传染的轮数或天数，A表示最终的人数．
【例12】（2022秋·湖南岳阳·九年级校考期中）新冠肺炎奥密克戎变异株自2021年底出现后，目前已成为全球流行的变异株，更是近期深圳感染的主要毒株，潜伏期更短，传播力更强，传播速度更快．变异株2分钟左右进入宿主细胞，分钟左右呈现指数复制，小时后释放成熟的病毒颗粒，通过气溶胶等方式进行传播．若有两个人患了该新冠肺炎，经过两轮传播后共有338个人被传染，那么每轮传染中平均一个人传染几个人（ ）
A．13B．11C．12D．14
【答案】C
【分析】根据题意可得第一轮人数加第二轮人数，再加第三轮人数总数为338人，设平均每人感染人，则列式为．即可解答．
【详解】解：设每轮传染中平均一个人传染了个人，
根据题意，得．
解得：或（舍去）．
∴每轮传染中平均一个人传染了12个人，
故选C．
【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
5.利润(销售)问题
利润(销售)问题中常用的等量关系：
利润=售价-进价(成本)
总利润=每件的利润×总件数
【例13】（2023·湖南长沙·统考模拟预测）为了推动长沙旅游业跨越发展，某旅行社推出“湖南博物院岳麓书院+橘子洲”一日游活动团队旅游收费标准：如果人数不超过人，人均费用为元；如果超过人，每增加人，人均费用降低元，但人均费用不得低于元．
(1)当旅游人数为人时，人均费用为元，求的取值范围；
(2)若某团队其支付旅游费用元，求该团队有多少人．
【答案】(1)
(2)人
【分析】（1）直接表示出人均费用，进而得出答案；
（2）根据题意可得人数超过了人，等量关系为：（人均旅游费用超过人的人数）人数，把相关数值代入求得人均旅游费用不得低于元的旅游方案即可．
【详解】（1）解：∵，
∴当人均费用为元时，人数一定超过人
∴，
解得：，
∴当时，人均费用为元；
（2）解：设该团队这次旅游共有人．
∵，
∴人数一定超过人，
∴，
∴，
整理得，
解得：，，
当时，，符合题意；
当时，，故舍去．
答：该团队有人．
【点睛】本题考查了一元一次方程与实际问题，一元二次方程与实际问题，读懂题意找出数量关系和等量关系是解题的关键．
【变式】（2022秋·陕西咸阳·九年级统考期中）今年某村农产品喜获丰收，该村村委会在网上直播销售A、B两种优质农产品礼包．
(1)已知今年7月份销售A种农产品礼包256包，8、9月该礼包十分畅销，销售量持续走高，在售价不变的基础上，9月份的销售量达到400包．若设8、9两个月销售量的月平均增长率为x，求x的值；
(2)若B种农产品礼包每包成本价为16元，当售价为每包30元时，每月销量为200包．为了尽快减少库存，该村准备在10月进行降价促销，经调查发现，若B种农产品礼包每包每降价1元，月销售量可增加20包，当B种农产品礼包每包降价多少元时，该村销售B种农产品礼包在10月份可获利2860元?
【答案】(1)的值为25%
(2)当B种农产品礼包每包降价3元时，该村销售B种农产品礼包在10月份可获利2860元
【分析】（1）利用9月份的销售量=7月份的销售量月平均增长率，即可得出关于x的一元二次方程，解之取其正值即可得出x的值；
（2）设B种农产品礼包每包降价m元，则每包的销售利润为元，月销售量为包，利用总利润=每包的销售利润×月销售量，即可得出关于m的一元二次方程，解之取其正值即可得出结论．
【详解】（1）依题意得：，
解得：，（不合题意，舍去）．
答：的值为25%．
（2）设B种农产品礼包每包降价m元，则每包的销售利润为元，月销售量为包，依题意得：，
整理得：，
解得：，.
∵为了尽快减少库存，
∴．
答：当B种农产品礼包每包降价3元时，该村销售B种农产品礼包在10月份可获利2860元．
【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
6、动态几何类问题：
（1）若动态图形比较特殊，思考用基本几何图形的面积公式找等量关系列方程或函数关系式；
（2）如动态图形不特殊，则思考用组合图形的面积和差找等量关系列方程或函数关系式
【例14】（2023秋·全国·九年级专题练习）如图，在中，，，，点从点开始沿边向点以的速度移动，点从点开始沿向点以的速度移动，当点到达点时，均停止运动，若的面积等于，则运动时间为（ ）
A．秒B．秒C．秒或秒D．秒或秒
【答案】A
【分析】根据题意当运动时间为秒时，，则，，可用含的式子表示的面积，列方程求解即可．
【详解】解：当运动时间为秒时，，则，，
根据题意得：，即，整理得：，解得：，，
当时，，不符合题意，舍去，
∴，
∴运动时间为秒，
故选：．
【点睛】本题主要考查动点与几何图形的综合，理解动点运动的规律，掌握几何图形面积的计算方法，解一元二次方程的方法等是解题的关键．
【变式】（2022秋·江苏连云港·九年级统考期中）小华同学学习了课本节“问题6”后，在已知条件不变的情况下，又对该例题进行了拓展探究，请你和他一起解决以下几个问题：

问题6如图，在矩形中，，，点P从点A出发沿以的速度向点B移动，同时，点Q从点B出发沿以的速度向点C移动．
(1)几秒钟后点P、Q的距离为？请说明理由；
(2)几秒钟后为直角？请说明理由；
(3)当时，内有一个动点M，连接、．若，线段的最小值为______．
【答案】(1)2秒或秒后，点P、Q的距离为，理由见解析；
(2)秒或6秒后，为直角，理由见解析；
(3)
【分析】（1）设运动时间为秒，则，，，利用勾股定理列方程求解，即可得到答案；
（2）设运动时间为秒，则，，，，利用勾股定理分别表示出、、，再利用勾股定理列方程求解，即可得到答案；
（3）设运动时间为秒，根据题意求出，进而得到，取的中点N，连接、，先证明直角三角形，进而得到，再利用勾股定理，求得，最后根据两点间线段最短，得到的最小值，即可求出线段的最小值．
【详解】（1）解：设运动时间为秒，
，，
，
，
四边形是矩形，
，
由勾股定理得：，
，
，
整理得：
解得：或，
2秒或秒后，点P、Q的距离为；
（2）解：设运动时间为秒，
，，
四边形是矩形，
，，，
，，
在中，，
在中，，
在中，，
为直角，
由勾股定理得：，
，
整理得：，即
解得：或，
秒或6秒后，为直角；
（3）解：设运动时间为秒，则，，
，
，
解得：，
，
如图，取的中点N，连接、，

，
，
，
，
，
点N是的中点，
，
在中，，
，即、、三点共线，有最小值，最小值为的长，
的最小值为，
故答案为：．
【点睛】本题属于四边形综合题，考查了矩形的性质，勾股定理，直角三角形斜边中线的性质，解一元二次方程，最短线段问题等知识，灵活运用所学知识解决问题是解题关键，属于中考常考题型．
7.形积问题
此类问题属于几何图形的应用问题，解决问题的关键是将不规则图形分割或组合成规则图形，根据图形的面积或体积公式，找出未知量与已知量的内在关系并列出方程.
【例15】（2023秋·全国·九年级专题练习）某校在操场东边开发出一块长、宽分别为、的矩形菜园（如图），作为劳动教育系列课程的实验基地之一，为了便于管理，现要在中间开辟一横两纵三条等宽的小道，剩下的用于种植，且种植面积为，设小道的宽为，根据题意可列方程为（ ）
​
A．B．
C．D．
【答案】A
【分析】由小道的宽为米，可得出种植菜园的部分可合成长为，宽为的长方形，再根据种植面积为，即可得出关于的一元二次方程，此题得解．
【详解】解：∵设小道的宽为，
∴剩下的用于种植的部分可合成长为，宽为的矩形，
根据题意得：，
故选：A．
【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
【变式】（2022秋·河南南阳·九年级统考期中）如图，学校要搭建一个矩形车棚，一边靠墙，在与墙正对的一面开了两个门．已知每个门宽度都是米，三边围栏材料的总长为米．

(1)如果要使车棚的面积为平方米，且尽量使靠墙的边长一些，那么垂直墙的一边长度应为多少米？
(2)这个车棚的面积能否达到平方米？
【答案】(1)垂直墙的一边长度应为米
(2)这个车棚的面积不能达到平方
【分析】（1）设垂直墙的一边长为米，根据题意列方程解方程即可；
（2）假设能使车棚的面积达到平方米，设这时垂直墙的一边长为米，根据题意列方程解方程即可．
【详解】（1）解：设垂直墙的一边长为米，则依题意，得
，
整理，得，
解这个方程，得，，
∵尽量使靠墙的边长一些，即尽量使垂直墙的一边小一些，
∴应取．
答：垂直墙的一边长度应为米；
（2）解：假设能使车棚的面积达到平方米，设这时垂直墙的一边长为米，则依题意，得
，
整理，得，
∵，
∴该方程没有实数解，即在实数范围内，不存在一个值，使矩形的面积为平方米．
【点睛】本题考查了一元二次方程与实际问题，读懂题意明确题目中的数量关系和等量关系是解题的关键．
8.图表问题
【例16】（2022春·全国·九年级期末）某电厂规定，该厂家属区的每户居民如果一个月的用电量不超过度，那么这个月这户居民只交10元电费；如果超过度，这个月除了交10元电费外，超过部分按每度元交费．
(1)该厂某户居民1月份用电90度，超过了度的规定，试写出超过部分应交的电费．（用含的代数式表示）
(2)下表是这户居民2月、3月的用电情况，请根据其中的数据，求电厂规定的度是多少．
【答案】(1)x（90－x）元
(2)50度
【分析】（1）根据题意可得用电90度超过了规定度数（90－x）度，再由超过部分按每度元交电费，即可求解；
（2）根据题意可得2月份用电量超过x度，列出方程，再由3月份用电45度只交电费10元，可得x≥45，即可求解．
【详解】（1）解：∵规定用电x度，
∴用电90度超过了规定度数（90－x）度，
∵超过部分按每度元交电费，
∴超过部分应交的电费为x（90－x）元．
（2）解∶2月份用电量超过x度，依题意得
x（80－x）＝25－10．
整理得x2－80x＋1500＝0．
解这个方程得x1＝30，x2＝50．
根据题意得：3月份用电45度只交电费10元，
∴电厂规定的x≥45，
∴x1＝30不合题意，舍去．
∴x＝50．
答：电厂规定的x度为50度．
【点睛】本题主要考查了一元二次方程的应用，明确题意，准确得到等量关系是解题的关键．
9.行程问题
【例17】（2023秋·重庆开州·九年级统考期末）随着人们对健康生活的追求，全民健身意识日益增强，徒步走成为人们锻炼的日常，中老年人尤为喜爱．
(1)张大伯徒步走的速度是李大伯徒步走的倍，张大伯走分钟，李大伯走分钟，共走米，求张大伯和李大伯每分钟各走多少米？
(2)天气好，天色早，张大伯和李大伯锻炼兴致很浓，又继续走，与（1）中相比，张大伯的速度不变，李大伯的速度每分钟提高了米，时间都各自多走了分钟，结果两人又共走了米，求的值．
【答案】(1)张大伯每分钟走米，李大伯每分钟走米
(2)的值为
【分析】（1）设李大伯徒步走的速度为每分钟米，则张大伯每分钟走米，根据两人共走了米列方程，解得的值代入中计算即可；
（2）结合（1）中所求可得到李大伯提高速度后每分钟走米，由已知条件可得张大伯走了分钟，李大伯走了分钟，根据两人又共走了米列方程，解方程并根据实际意义确定值即可．
【详解】（1）解：设李大伯徒步走的速度为每分钟米，得
解得
∴（米）
所以，张大伯每分钟走米，李大伯每分钟走米；
（2）解：依题意，得
整理得
解得（舍），
答：的值为．
【点睛】本题考查了列一元一次方程解决问题，列一元二次方程解决问题，正确找到数量关系是解决问题的关键．
10.工程问题
【例18】（2022秋·四川达州·九年级校考期中）公安部交管局部署“一盔一带”安全守护行动，带动了市场头盔的销量．某头盔经销商5至7月份统计，某品牌头盔5月份销售2250个，7月份销售3240个，且从5月份到7月份销售量的月增长率相同．请解决下列问题．
(1)求该品牌头盔销售量的月增长率；
(2)为了达到市场需求，某工厂建了一条头盔生产线生产头盔，经过一段时间后，发现一条生产线最大产能是900个/天，但如果每增加一条生产线，每条生产线的最大产能将减少30个/天，现该厂要保证每天生产头盔3900个，在增加产能同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？
【答案】(1)该品牌头盔销售量的月增长率为20%
(2)在增加产能同时又要节省投入的条件下，增加4条生产线
【分析】（1）设该品牌头盔销售量的月增长率为x，根据题意列出一元二次方程进行求解；
（2）设增加x条生产线，根据条件列出一元二次方程求解，再根据要节省投入的条件下，确定解．
【详解】（1）解：设该品牌头盔销售量的月增长率为x．
依题意，得：，
解得：，（不合题意，舍去）．
答：该品牌头盔销售量的月增长率为20%．
（2）解：设增加x条生产线．
，
解得，（不符合题意，舍去），
答：在增加产能同时又要节省投入的条件下，增加4条生产线．
【点睛】本题考查了一元二次方程的应用，解题的关键是根据题意列出相应的一元二次方程求解即可．
【变式】（2023秋·重庆合川·九年级统考期末）2022年暑期，我区遭遇连续高温和干旱，一居民小区的部分绿化树枯死．小区物业管理公司决定补种绿化树，计划购买小叶榕和香樟共50棵进行栽种．其中小叶榕每棵680元，香樟每棵1000元，经测算，购买两种树共需38800元．
(1)原计划购买小叶榕、香樟各多少棵？
(2)实际购买时，经物业管理公司与商家协商，每棵小叶榕和香樟的售价均下降元（），且两种树的售价每降低10元，物业管理公司将在原计划的基础上多购买小叶榕2棵，香樟1棵．物业管理公司实际购买的费用比原计划多3600元，求物业管理公司实际购买两种树共多少棵？
【答案】(1)原计划购买小叶榕35棵、香樟15棵
(2)物业管理公司实际购买两种树共56棵
【分析】（1）设原计划购买小叶榕棵，则购买香樟棵，根据题意列出方程即可得出答案．
（2）根据给出的条件先列出小叶榕与香樟的单价表达式分别为元每棵，元每棵，再列出实际购买棵树的表达式，得到方程式求出满足条件的值，即可得出答案．
【详解】（1）设原计划购买小叶榕棵，则购买香樟棵，
根据题意，可得，
解得，．
答：原计划购买小叶榕35棵、香樟15棵．
（2）根据题意，可得，
整理得，，
解得：，，
∵，∴，
∴购买了39棵小叶榕，17棵香樟，
答：物业管理公司实际购买两种树共56棵．
【点睛】本题主要考查一元一次方程的实际应用和一元二次方程应用的问题，熟练掌握题中的等量关系列出正确的方程解决本题的关键．
特别说明：
列一元二次方程解应用题是把实际问题抽象为数学问题（列方程），然后由数学问题的解决而获得对实际问题的解决.这是在解决实际问题时常用到的数学思想—方程思想
【规律方法】列一元二次方程解应用题的“六字诀”
1．审：理解题意，明确未知量、已知量以及它们之间的数量关系．
2．设：根据题意，可以直接设未知数，也可以间接设未知数．
3．列：根据题中的等量关系，用含所设未知数的代数式表示其他未知量，从而列出方程．
4．解：准确求出方程的解．
5．验：检验所求出的根是否符合所列方程
6. 答 (写出答案，切忌答非所问).
月份
用电量/度
交电费总数/元
2月
80
25
3月
45
10