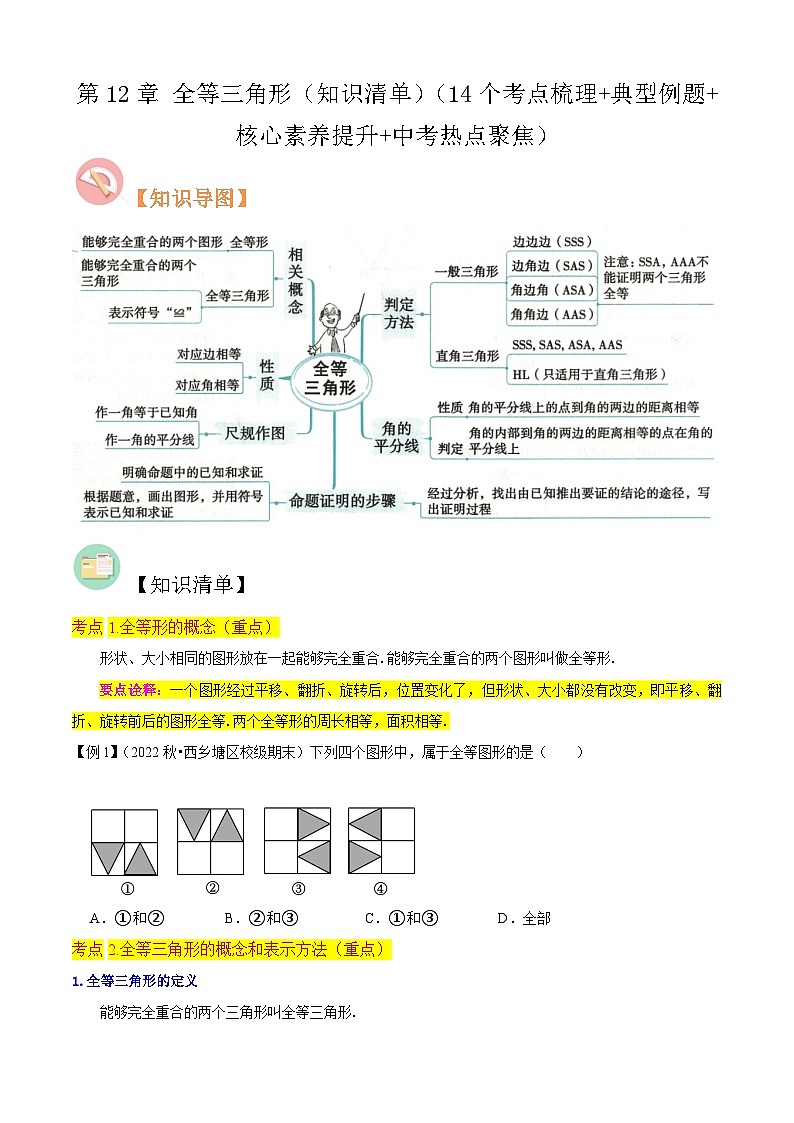




第12章 全等三角形(知识清单)(14个考点梳理+典型例题+核心素养提升+中考热点聚焦)-2023-2024学年八年级数学上学期期中期末考点大串讲(人教版)
展开【知识清单】
考点1.全等形的概念(重点)
形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.
要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.
【例1】(2022秋•西乡塘区校级期末)下列四个图形中,属于全等图形的是( )
A.①和②B.②和③C.①和③D.全部
【解答】解:①、②、③和④可以完全重合的,因此全等的图形是①和②③④.
故选:D.
考点2.全等三角形的概念和表示方法(重点)
1.全等三角形的定义
能够完全重合的两个三角形叫全等三角形.
2. 对应顶点,对应边,对应角定义
两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.
要点诠释:
在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
3. 找对应边、对应角的方法
(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;
(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;
(3)有公共边的,公共边是对应边;
(4)有公共角的,公共角是对应角;
(5)有对顶角的,对顶角一定是对应角;
(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.
【例2】(2022秋·辽宁大连·八年级统考期中)下列说法正确的是( )
A.两个直角三角形一定全等B.形状相同的两个三角形全等
C.全等三角形的面积一定相等D.面积相等的两个三角形全等
【答案】C
【详解】解:A、两个直角三角形不一定全等,故错误,不符合题意;
B、形状相同的两个三角形不一定全等,故错误,不符合题意;
C、全等三角形的面积一定相等,故正确,符合题意;
D、面积相等的两个三角形不一定全等,故错误,不符合题意;
考点3全等三角形的性质(重点)
全等三角形的对应边相等;
全等三角形的对应角相等.
要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.
【例3】(2023春·山东济南·七年级统考期末)如图,,若,则的长度为( )
A.2B.5C.10D.15
【答案】C
【分析】根据全等三角形的性质得到即可求解.
【详解】∵,,
∴,
∴,
故选:C.
【点睛】本题考查全等三角形的性质,熟记全等三角形对应边相等是解题的关键.
考点4.三角形全等的基本事实:边边边(重点)
三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
要点诠释:如图,如果=AB,=AC,=BC,则△ABC≌△.
【例4】(2022秋·福建龙岩·八年级校联考期中)如图,,,求证:.
【分析】根据三条边都对应相等的两个三角形是等边三角形即可证明.
【详解】证明:在和中,
,
∴
∴.
【点睛】本题考查了全等三角形的判定——边边边,熟练掌握全等三角形的判定和性质是解题的关键.
考点5.用直尺和圆规作一个角等于已知角
【例5】(2023春·安徽宿州·八年级校考期中)已知,求作.(不要求写作法,但是必须保留作图痕迹)
【分析】(1)首先画射线,(2)以顶点为圆心,任意长为半径画弧,交两边于E、D,(3)以O为圆心,长为半径画弧,交与点N,(4)再以N为圆心,长为半径画弧,交前弧于点M,画射线.
【详解】解:如图所示:.
.
【点睛】此题主要考查了作一个角等于已知角的基本作图,关键是熟练掌握基本作图的方法.
考点6.三角形全等的基本事实:边角边(重点)
1. 全等三角形判定——“边角边”
两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
要点诠释:如图,如果AB = ,∠A=∠,AC = ,则△ABC≌△. 注意:这里的角,指的是两组对应边的夹角.
2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.
如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.
【例6】(2023春·四川达州·七年级校考期末)如图,由,,,得的根据是( )
A.SASB.ASAC.AASD.SSS
【答案】A
【分析】由已知得到,即可利用“”证明.
【详解】解:,
,
,
在和中,
,
,
故选:A.
【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的一般判定方法是解题关键.
考点7.三角形全等的基本事实:角边角(重点)
两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).
要点诠释:如图,如果∠A=∠,AB=,∠B=∠,则△ABC≌△.
考点8.三角形全等的推论:角角边(重点)
1.全等三角形判定——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图,在△ABC和△ADE中,如果DE∥BC,那么∠ADE=∠B,∠AED=∠C,又∠A=∠A,但△ABC和△ADE不全等.这说明,三个角对应相等的两个三角形不一定全等.
【例7】(2021秋·辽宁盘锦·八年级校考期中)如图,,,连接交于点O,点E,F在线段上,且.求证:.
【分析】利用已知条件证明,推出,由,得到,即.
【详解】证明:∵,
∴,
在和中,,
∴,
∴,
∵,
∴,
即.
【点睛】此题考查全等三角形的性质与判定,解题的关键是证明.
考点9.直角三角形全等的判定方法:HL(重点)
【例8】.(2023春·广东梅州·八年级校考期中)已知:如图,、是的高,且.求证:.
【分析】根据、是的高得到直角,再证明≌即可得到结论.
【详解】证明:、是的高,
,,
,
在和中,
,
≌,
.
【点睛】本题考查全等三角形的性质和判定,利用证明直角三角形全等是本题关键.
考点10.常见全等三角形的基本图形
1、截长补短
有一类几何题其命题主要证明三条线段长段的“和”或“差”及其比例关系,这一类题目一般可以采取“截长”或“补短”的方法来进行求解。所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已经线段相等,然后证明其中的另一段与已知的另一段的大小关系。所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段关系。有的是采取截长补短后,使之构成某种特定的三角形进行求解。
2、倍长中线
图一
图二
图三
3、过端点向中线作垂线
一线三等角
模型 三垂直全等模型
图一
如图一,∠D=∠BCA=∠E=90°,BC=AC。 结论:Rt△BDC≌Rt△CEA
图二
如图二,∠D=∠BCA=∠E,BC=AC。 结论:△BEC≌△CDA
5、手拉手
图一 图二
图三 图四 图五
图六 图七
手拉手模型的定义:
定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)
如右图:手拉手模型的重要结论:
结论1:∆ABC≅∆A/B/C/(SAS)
BC=B/C/(左手拉左手等于右手拉右手)
结论2:∠BOB=∠BAB(利用三角形全等及顶角相等
的等腰三角形底角相等)
结论3:AO平分∠BOC/(利用三角形全等面积相等,再利用角平分线性质定理证明)
【例9】(2023春·山东枣庄·八年级校考期中)如图(1),已知中,,,是过A的一条直线,且在的异侧,于D,于E.
(1)试说明:.
(2)若直线绕A点旋转到图2位置时(),其余条件不变,问与的关系如何?请直接写出结果;
(3)若直线绕A点旋转到图3位置时(),其余条件不变,问与、的关系如何?请直接写出结果,不需说明.
【答案】(1)见解析
(2)
(3)
【分析】(1)证明,即可证得,,而,即可证得;
(2)证明,即可证得,,而,即可证得;
(3)证明,即可证得,,而,即可证得.
【详解】(1)证明:∵,,
∴,
∵,
∴,
∴,
又∵,,
∴,
∴,,
∴;
(2)解:;理由如下:
∵,,
∴,
∵,
∴,
∴,
又∵,,
∴,
∴,,
∴;
(3)解:;理由如下:
∵,,
∴,
∵,
∴,
∴,
又∵,,
∴,
∴,,
∴.
【点睛】本题主要考查了全等三角形的判定和性质,余角的性质,解题的关键是熟练掌握三角形全等的判定方法,证明.
【例10】(2022秋·湖北孝感·八年级统考期中)已知:,,.
(1)如图1当点在上,______.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
【答案】(1)
(2),理由见解析
【分析】(1)由全等可知,所以当点在上时,为等腰三角形,依据已知计算即可.
(2)因为两个三角形中有一边相等,只要找到这两个底对应高之间的关系即可.
【详解】(1)解:,
,
又,,
,
在中,,
故答案为:.
(2)解:如下图所示:过点作的边上的高,过点作的边上的高,由作图及知:
,,,
(同角的余角相等),
在与中有:
(),
,
,,
,,
,
故答案为:.
【点睛】本题考查了全等三角形性质和判定,关键是使用分析法找到:两个三角形面积相等时,底相等则高相等,从而构造全等证明对应高相等.
考点11.作已知角的平分线(重点)
角平分线的尺规作图
(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.
(2)分别以D、E为圆心,大于DE的长为半径画弧,两弧在∠AOB内部交于点C.
(3)画射线OC.
射线OC即为所求.
【例11】(2023春·陕西榆林·七年级校考期末)如图,已知,利用尺规,在边上求作一点,使得.(保留作图痕迹,不写作法)
【详解】解:如图点即为所求.
.
考点12.角的平分线的性质(重点)
角的平分线的性质:角的平分线上的点到角两边的距离相等.
要点诠释:
用符号语言表示角的平分线的性质定理:
若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.
【例12】(2023春•普宁市校级期中)如图,AD是△ABC的角平分线,且DE⊥AB,∠B=50°,∠C=60°.
(1)求∠ADC的度数.
(2)若DE=5,点F是AC上的动点,求DF的最小值.
【解答】解:(1)∵∠B=50°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=70°,
∵AD是△ABC的角平分线,
∴,
∴∠ADC=∠B+∠BAD=85°;
(2)∵点F是AC上的动点,
∴当DF⊥AC时,DF最小,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DF=DE=5.
考点13.证明几何命题的一般步骤(难点)
(1)按题意画出图形.
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论
(3)在“证明”中写出推理过程
在解决几何问题时,有时需要添加辅助线.添辅助线的过程要写人证明中.辅助线通常画成虚线
【例13】(2022秋·山东德州·八年级校考期中)求证:三角形两外角的平分线的交点到三角形三边(或所在的直线)距离相等.
要求:画图,写出已知,求证,然后写出证明过程.
【详解】解;已知:如图,的外角平分线与外角平分线相交于点P.
求证:;
证明:如图,过点P作于F,于G,于H,
∵的外角平分线与相交于点P,
∴,,
∴.
即点P到三边、、所在直线的距离相等
∴三角形两外角的平分线的交点到三角形三边(或所在直线)的距离相等.
【例14】(2022春·甘肃酒泉·八年级统考期中)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,,点在上,______,求证:______.请你补全已知和求证.
(2)并写出证明过程.
【答案】(1),,垂足分别为、;
(2)证明见解析
【详解】(1)解:已知:如图,,点在上,,垂足分别为、;
求证:.
(2)证明:∵,,
∴,
在和中,
,
∴,
∴.
考点14.角的平分线的判定(重点)
角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.
要点诠释:
用符号语言表示角的平分线的判定:
若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB
【例15】(2023春•达川区期中)如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.
【解答】(1)解:结论:EC=BF,EC⊥BF.
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAF.
在△EAC和△BAF中,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF.
(2)证明:作AP⊥CE于P,AQ⊥BF于Q.
∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等).
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.
【核心素养提升】
逻辑推理——构建全等三角形进行证明
【例16】.(2023春·黑龙江佳木斯·八年级校考期中)如图,,,,求的度数.
【答案】
【分析】连接,由,,以及公共边,利用可得出三角形与三角形全等,由全等三角形的对应角相等得到,根据的度数即可求出的度数.
【详解】解:连接,如图所示:
在和中,
,
,
又,
.
【点睛】此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.
【例17】(2022秋·福建龙岩·八年级校考期中)如图,点E在线段AB上,,,.
求证:
(1);
(2).
【分析】(1)延长交的延长线于,根据平行线的性质和已知求出,推出,根据等腰三角形性质求出,证,求出即可.
(2)根据(1)可得,即可得到.
【详解】(1)延长交的延长线于,
∵,
,
,
,
,
,
,
在和中
,
,
即.
(2)根据(1)可得,
∴.
【点睛】本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质的应用,主要考查学生运用定理进行推理的能力,题目比较好,难度适中.
【例18】(2022秋·福建福州·八年级校考期中)(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在中,,,求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长到Q,使得;
②再连接,把集中在中;
③利用三角形的三边关系可得,则AD的取值范围是 .
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)请你写出图1中与的位置关系并证明.
(3)思考:已知,如图2,是的中线,,,.试探究线段与的数量和位置关系并加以证明.
【答案】(1);(2),证明见解析;(3),,证明见解析
【分析】(1)先证,推出,再利用三角形三边关系求解;
(2)根据可得,即可证明;
(3)同(1)可证,得出,,进而可得,推出,可得,,即可求解.
【详解】解:(1)是的中线,
,
又,,
,
,
在中,,
,即,
,
故答案为:;
(2),证明如下:
由(1)知,
,
;
(3),,证明如下:
如图,延长至点Q使得,连接,延长交于点P,
同(1)可得,
,,
,
,
,
,
,
,
,
,
在和中,
,
,
,,
,
,
,
,
,
,
,
,
,
综上可得,.
【点睛】本题考查全等三角形的判定和性质,平行线的判定和性质,三角形三边关系的应用等,解题的关键是通过倍长中线构造全等三角形.
【中考热点聚焦】
热点1.三角形全等的判定
1.(2023•衢州)已知:如图,在△ABC和△DEF中,B,E,C,F在同一条直线上.下面四个条件:
①AB=DE;②AC=DF;③BE=CF;④∠ABC=∠DEF.
(1)请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).
(2)在(1)的条件下,求证:△ABC≌△DEF.
【分析】(1)根据两三角形全等的判定定理,选择合适的条件即可.
(2)根据(1)中所选条件,进行证明即可.
【解答】解:(1)由题知,
选择的三个条件是:①②③;
或者选择的三个条件是:①③④.
证明:(2)当选择①②③时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
当选择①③④时,
∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
【点评】本题考查全等三角形的证明,熟知全等三角形的判定定理是解题的关键.
2.(2023•云南)如图,C是BD的中点,AB=ED,AC=EC.求证:△ABC≌△EDC.
【分析】求出BC=DC,根据全等三角形的判定定理证明即可.
【解答】证明:∵C是BD的中点,
∴BC=DC,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(SSS).
【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.
热点2.三角形全等的判定和性质的综合应用
3.(2023•苏州)如图,在△ABC中,AB=AC,AD为△ABC的角平分线.以点A圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.
(1)求证:△ADE≌△ADF;
(2)若∠BAC=80°,求∠BDE的度数.
【分析】(1)由角平分线定义得出∠BAD=∠CAD.由作图知:AE=AF.由SAS可证明△ADE≌△ADF;
(2)由作图知:AE=AD.得出∠AED=∠ADE,由等腰三角形的性质求出∠ADE=70°,则可得出答案.
【解答】(1)证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
由作图知:AE=AF.
在△ADE和△ADF中,
,
∴△ADE≌△ADF(SAS);
(2)解:∵∠BAC=80°,AD为△ABC的角平分线,
∴∠EAD=∠BAC=40°,
由作图知:AE=AD.
∴∠AED=∠ADE,
∴∠ADE=×(180°﹣40°)=70°,
∵AB=AC,AD为△ABC的角平分线,
∴AD⊥BC.
∴∠BDE=90°﹣∠ADE=20°.
【点评】本题考查了全等三角形的判定与性质,角平分线的性质,等腰三角形的性质,熟练掌握全等三角形的判定是解题的关键.
4.(2023•营口)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,∠ACE=∠BDF.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
【分析】(1)根据全等三角形的判定定理证明△ACE≌△DBF即可;
(2)根据全等三角形的性质即可得到结论.
【解答】(1)证明:在△ACE和△BDF中,
,
∴△ACE≌△BDF(AAS);
(2)由(1)知△ACE≌△BDF,
∴BD=AC=2,
∵AB=8,
∴CD=AB﹣AC﹣BD=4,
故CD的长为4.
【点评】此题主要考查了全等三角形的判定与性质;熟练掌握证明三角形全等是解决问题的关键.
5.(2023•南通)如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC.
求证:∠1=∠2.
小虎同学的证明过程如下:
(1)小虎同学的证明过程中,第 二 步出现错误;
(2)请写出正确的证明过程.
【分析】(1)根据全等三角形的判定定理判断;
(2)证明△DOB≌△EOC,根据全等三角形的性质得到OD=OE,再证明Rt△ADO≌Rt△AEO,得到∠1=∠2.
【解答】(1)解:小虎同学的证明过程中,第二步出现错误,
故答案为:二;
(2)证明:∵∠ADC=∠AEB=90°,
∴∠BDC=∠CEB=90°,
在△DOB和△EOC中,
,
∴△DOB≌△EOC(AAS),
∴OD=OE,
在Rt△ADO和Rt△AEO中,
,
∴Rt△ADO≌Rt△AEO(HL),
∴∠1=∠2.
【点评】本题考查的是全等三角形的判定和性质,掌握三角形全等的判定定理是解题的关键.
6.(2023•陕西)如图,在△ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
【分析】利用三角形内角和定理得∠CAB的度数,再根据全等三角形的判定与性质可得结论.
【解答】证明:在△ABC 中,∠B=50°,∠C=20°,
∴∠CAB=180°﹣∠B﹣∠C=110°.
∵AE⊥BC.
∴∠AEC=90°.
∴∠DAF=∠AEC+∠C=110°,
∴∠DAF=∠CAB.
在△DAF和△CAB中,
,
∴△DAF≌△CAB(SAS).
∴DF=CB.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
7.(2023•长沙)如图,AB=AC,CD⊥AB,BE⊥AC,垂足分别为D,E.
(1)求证:△ABE≌△ACD;
(2)若AE=6,CD=8,求BD的长.
【分析】(1)利用“AAS”可证明△ABE≌△ACD;
(2)先利用全等三角形的性质得到AD=AE=6,再利用勾股定理计算出AC,从而得到AB的长,然后计算AB﹣AD即可.
【解答】(1)证明:∵CD⊥AB,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS);
(2)解:∵△ABE≌△ACD,
∴AD=AE=6,
在Rt△ACD中,AC===10,
∵AB=AC=10,
∴BD=AB﹣AD=10﹣6=4.
【点评】本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
8.(2023•聊城)如图,在四边形ABCD中,点E是边BC上一点,且BE=CD,∠B=∠AED=∠C.
(1)求证:∠EAD=∠EDA;
(2)若∠C=60°,DE=4时,求△AED的面积.
【分析】(1)利用AAS证明∴△ABE≌△ECD,即可证明结论;
(2)先证明△AED为等边三角形,可得AE=AD=ED=4,过A点作AF⊥ED于F,利用等边三角形的性质可得EF=2,再根据勾股定理求得AF的长,利用三角形的面积公式可求解.
【解答】(1)证明:∵∠B=∠AED=∠C,∠AEC=∠B+∠BAE=∠AED+∠CED,
∴∠BAE=∠CED,
在△ABE和△ECD中,
,
∴△ABE≌△ECD(AAS),
∴AE=ED,
∴∠EAD=∠EDA;
(2)解:∵∠AED=∠C=60°,AE=ED,
∴△AED为等边三角形,
∴AE=AD=ED=4,
过A点作AF⊥ED于F,
∴EF=ED=2,
∴AF=,
∴S△AED=ED•AF=.
【点评】本题主要考查全等三角形的判定与性质,等边三角形的判定与性质,勾股定理,三角形的面积等知识的综合运用,证明△ABE≌△ECD是解题的关键.
热点3.三角形全等的实际应用
9.(2022•扬州)如图,小明家仿古家具的一块三角形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CAB.AB,BC,∠BC.AB,AC,∠BD.∠A,∠B,BC
【分析】直接利用全等三角形的判定方法分析得出答案.
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
【点评】此题主要考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
10.(2022•百色)校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD,其中AB=CD=2米,AD=BC=3米,∠B=30°.
(1)求证:△ABC≌△CDA;
(2)求草坪造型的面积.
【分析】(1)利用全等三角形的判定方法,结合三边关系得出答案;
(2)直接利用全等三角形的性质以及直角三角形中30度所对边与斜边的关系的得出对应边长,进而得出答案.
【解答】(1)证明:在△ABC和△CDA中,
∵,
∴△ABC≌△CDA(SSS);
(2)解:过点A作AE⊥BC于点E,
∵AB=2米,∠B=30°,
∴AE=1米,
∴S△ABC=×3×1=(平方米),
则S△CDA=(平方米),
∴草坪造型的面积为:2×=3(平方米).
【点评】此题主要考查了全等三角形的判定与性质以及全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
热点4.角的平分线的性质
11.(2023•广州)如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,AE=12,DF=5,则点E到直线AD的距离为 .
【分析】过E作EH⊥AD于H,由角平分线的性质得到DE=DF=5,由勾股定理求出AD==13,由三角形面积公式得到13EH=12×5,因此EH=,即可得到点E到直线AD的距离.
【解答】解:过E作EH⊥AD于H,
∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF=5,
∵AE=12,
∴AD==13,
∵△ADE的面积=AD•EH=AE•DE,
∴13EH=12×5,
∴EH=,
点E到直线AD的距离为.
故答案为:.
【点评】本题考查角平分线的性质,三角形的面积,勾股定理,关键是由三角形的面积得到AD•EH=AE•DE.
12.(2022•北京)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S△ACD= .
【分析】过D点作DH⊥AC于H点,如图,根据角平分线的性质得到DE=DH=1,然后根据三角形面积公式计算.
【解答】解:过D点作DH⊥AC于H点,如图,
∵AD平分∠BAC,DE⊥AB,DH⊥AC,
∴DE=DH=1,
∴S△ACD=×2×1=1.
故答案为:1.
【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.
证明:∵∠ADC=∠AEB=90°,
∴∠DOB+∠B=∠EOC+∠C=90°.
∵∠DOB=∠EOC,
∴∠B=∠C.……第一步
又OA=OA,OB=OC,
∴△ABO≌△ACO.……第二步
∴∠1=∠2.……第三步
清单05 分式(23个考点梳理+题型解读+核心素养提升+中考聚焦)-八年级上学期数学期末考点大串讲(人教版): 这是一份清单05 分式(23个考点梳理+题型解读+核心素养提升+中考聚焦)-八年级上学期数学期末考点大串讲(人教版),文件包含清单05分式23个考点梳理+题型解读+核心素养提升+中考聚焦原卷版docx、清单05分式23个考点梳理+题型解读+核心素养提升+中考聚焦解析版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
清单03 轴对称(16个考点梳理+典型例题+核心素养提升+中考热点聚焦)-八年级上学期数学期末考点大串讲(人教版): 这是一份清单03 轴对称(16个考点梳理+典型例题+核心素养提升+中考热点聚焦)-八年级上学期数学期末考点大串讲(人教版),文件包含清单03轴对称16个考点梳理+典型例题+核心素养提升+中考热点聚焦原卷版docx、清单03轴对称16个考点梳理+典型例题+核心素养提升+中考热点聚焦解析版docx等2份试卷配套教学资源,其中试卷共87页, 欢迎下载使用。
清单02 全等三角形(8个考点梳理+题型解读+核心素养提升+中考聚焦)-八年级上学期数学期末考点大串讲(人教版): 这是一份清单02 全等三角形(8个考点梳理+题型解读+核心素养提升+中考聚焦)-八年级上学期数学期末考点大串讲(人教版),文件包含清单02全等三角形8个考点梳理+题型解读+核心素养提升+中考聚焦原卷版docx、清单02全等三角形8个考点梳理+题型解读+核心素养提升+中考聚焦解析版docx等2份试卷配套教学资源,其中试卷共59页, 欢迎下载使用。












