广东省广州市黄埔区2021-2022学年七年级上学期期末数学试题（原卷版）

这是一份广东省广州市黄埔区2021-2022学年七年级上学期期末数学试题（原卷版），文件包含单元质量评价六第6章试卷教师版2023-2024沪教版化学九年级下册docx、单元质量评价六第6章试卷学生版2023-2024沪教版化学九年级下册docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

1 如果把一个物体向右移动1m时记作移动+1m，那么这个物体向左移动2m时记作移动（ ）
A. ﹣1mB. +2mC. ﹣2mD. +3m
【答案】C
【解析】
【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
【详解】解：如果把一个物体向右移动1m时记作移动+1m，那么这个物体向左移动2m时记作移动-2m，
故选：C．
【点睛】本题考查了正数和负数，解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．
2. 下列各式正确的是（ ）
A. |﹣3|＝|3|B. |﹣3|＝﹣|3|C. |﹣3|＝﹣3D.
【答案】A
【解析】
【分析】直接利用绝对值的性质分别化简得出答案．
详解】解：A、|-3|=3和|3|=3，数值相等，符合题意；
B、|-3|=3和-|3|=-3，数值不相等，不符合题意；
C、|-3|=3≠-3，数值不相等，不符合题意；
D、|-3|=3≠，数值不相等，不符合题意；
故选：A．
【点睛】本题主要考查了绝对值的性质，正确化简各数是解题关键．
3. 比a的3倍大5的数等于a的4倍，则下列等式正确的是（ ）
A. 3a﹣5＝4aB. 3a+5＝4aC. 5﹣3a＝4aD. 3（a+5）＝4a
【答案】B
【解析】
【分析】先列代数式，再列方程即可．
【详解】解：∵比a的3倍大5的数为3a+5，a的4倍为4a，
∴根据题意得3a+5=4a．
故选择B．
【点睛】本题考查列代数式，列方程，掌握列代数式，列方程技巧与方法是解题关键．
4. 已知amb2与是同类项，则m﹣n＝（ ）
A. 2B. ﹣1C. 1D. 3
【答案】B
【解析】
【分析】根据同类项定义：所含字母相同，相同字母的指数也相同的项是同类项求出m=1，n=2，然后求代数式的值即可．
【详解】解：∵amb2与是同类项，
∴m=1，n=2，
当m=1，n=2时，m﹣n＝1-2=-1．
故选择B．
【点睛】本题考查同类项定义，代数式的值，掌握同类项定义，代数式的值的步骤是解题关键．
5. 中国的陆地面积约为，这个面积用科学记数法表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据科学记数法的表示方法写出即可．
【详解】解：将9600000用科学记数法表示为9.6×106．
故选：C．
【点睛】本题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤a＜10，n为整数，表示时关键要正确确定a的值以及n的值．
6. 如图所示为几何体的平面展开图，则从左到右，其对应的几何体名称分别为( )
A. 圆锥，正方体，三棱锥，圆柱B. 正方体，圆锥，四棱锥，圆柱
C. 正方体，圆锥，四棱柱，圆柱D. 正方体，圆锥，圆柱，三棱柱
【答案】D
【解析】
【分析】根据常见几何体的平面展开图判断即可．
【详解】解：根据几何体的平面展开图，则从左到右，其对应的几何体名称分别为：正方体，圆锥，圆柱，三棱柱．
故选D．
【点睛】本题考查了常见几何体的展开图；熟记常见几何体的平面展开图的特征，是解决此类问题的关键．
7. 下列整式运算错误的是（ ）
A. ﹣ab+2ba＝ab
B. 3a2b+2ab2﹣（5a2b+ab2）＝﹣ab2
C. ﹣2（3﹣x）＝﹣6+2x
D. m﹣n2+m﹣n2＝2m﹣2n2
【答案】B
【解析】
【分析】根据整式的加减混合运算法则依次计算判断即可得．
详解】解：A、，选项计算正确；
B、，选项计算错误；
C、，选项计算正确；
D、，选项计算正确；
故选：B．
【点睛】题目主要考查整式的加减混合运算，熟练掌握运算法则是解题关键．
8. 下列是根据等式的性质进行变形，正确的是（ ）
A. 若ax＝ay，则x＝yB. 若a﹣x＝b+x，则a＝b
C. 若x＝y，则x﹣5＝y+5D. 若，则x＝y
【答案】D
【解析】
【分析】根据等式的性质逐个判断即可．
【详解】A．当时，ax＝ay，不能推出x＝y，故本项不符合题意．
B．等式两边同时加上x，得，故本项不符合题意．
C．因为x＝y，所以x+5＝y+5，故本项不符合题意．
D．因为，当等式两边同时乘以4，得x＝y，故本项符合题意．
【点睛】本题考查了等式得性质，能熟记等式的性质是解决此题的关键，等式两边同时加或减同一个数或式子，等式仍然成立；等式两边乘同一个数，等式仍成立；等式两边同时除以一个不为0的数，等式仍然成立．
9. 如图，BD在∠ABC的内部，∠ABD＝∠CBD，如果∠ABC＝80°，则∠ABD＝（ ）
A. B. 20°C. 60°D.
【答案】B
【解析】
【分析】根据角的和差与倍分得出∠ABC=4∠ABD，列方程求解即可．
【详解】解：∵∠ABD＝∠CBD，
∴∠CBD=3∠ABD，
∵∠ABC=∠CBD+∠ABD=3∠ABD+∠ABD=4∠ABD=80°，
∴ABD=20°．
故选择B．
【点睛】本题考查角的倍分，角的和差，一元一次方程，掌握角的倍分关系，角的和差计算，解一元一次方程是解题关键．
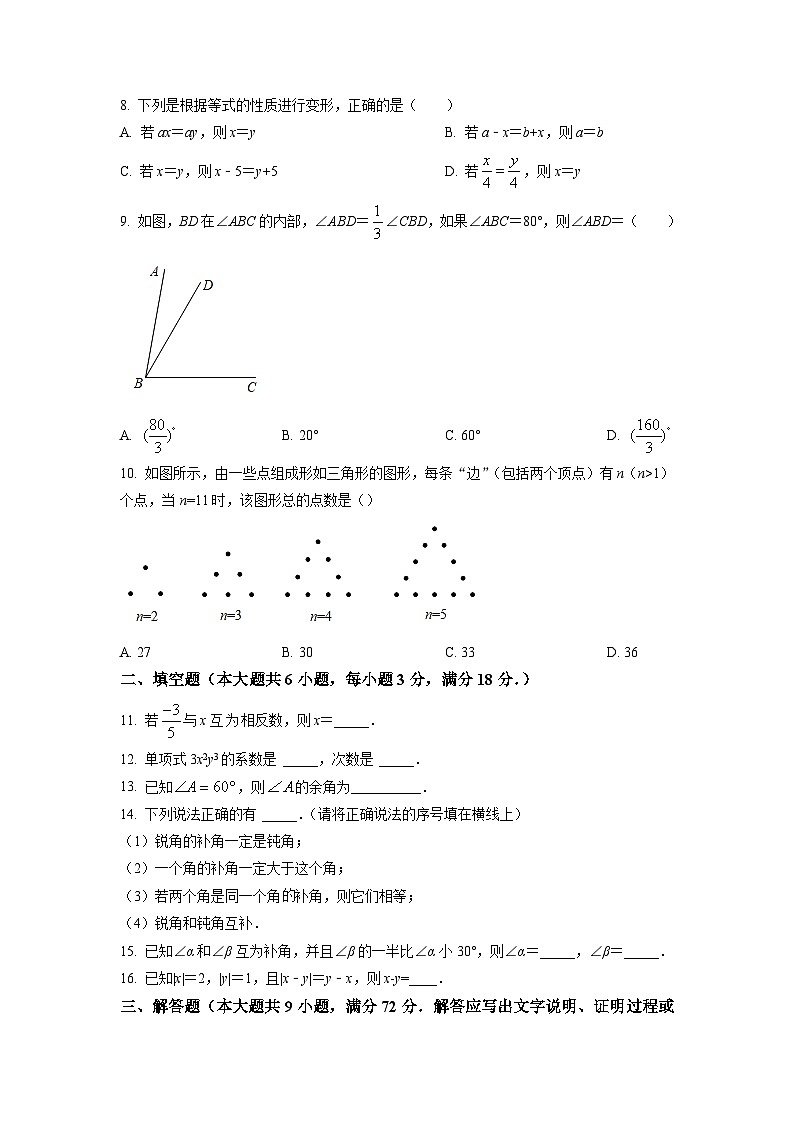
10. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有n（n>1）个点，当n=11时，该图形总的点数是（）
A 27B. 30C. 33D. 36
【答案】B
【解析】
【分析】从第一个图形分析已知的图形中点的个数的计算方法，得出变化规律进而求出即可．
【详解】解：当n=2时，有3×2-3=3个点，
当n=3时，有3×3-3=6个点，
当n=4时，有4×3-3=9个点，
…
第n个图形中有3n-3个点，
当n=11时，3n-3=3×11-3=30．
故选：B．
【点睛】本题主要考查了图形的变化类，根据已知的图形中点数的变化得出规律是解题关键．
二、填空题（本大题共6小题，每小题3分，满分18分．）
11. 若与x互为相反数，则x＝_____．
【答案】##0.6
【解析】
【分析】根据相反数的定义（只有符号不同的两个数互为相反数）求解即可得．
【详解】解：∵x与互为相反数，
∴，
故答案为：．
【点睛】题目主要考查相反数的定义，深刻理解相反数的定义是解题关键．
12. 单项式3x2y3的系数是 _____，次数是 _____．
【答案】 ①. 3 ②. 5
【解析】
【分析】根据单项式的系数和次数的概念解答即可．
【详解】解：单项式3x2y3的系数是3，次数是5，
故答案为：3；5．
【点睛】本题考查的是单项式的系数和次数的概念，单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数．
13. 已知，则的余角为__________．
【答案】30°
【解析】
【分析】本题考查角互余的概念：和为90度的两个角互为余角．
【详解】解：根据定义∠A的余角度数是90°-60°=30°．
故答案为30°.
【点睛】此题考查余角，属于基础题，较简单，主要记住互为余角的两个角的和为90度．
14. 下列说法正确的有 _____．（请将正确说法的序号填在横线上）
（1）锐角的补角一定是钝角；
（2）一个角的补角一定大于这个角；
（3）若两个角是同一个角的补角，则它们相等；
（4）锐角和钝角互补．
【答案】（1）（3）##（3）（1）
【解析】
【分析】根据余角与补角的定义，即可作出判断．
【详解】解：（1）锐角的补角一定是钝角，故（1）正确；
（2）一个角的补角不一定大于这个角；
∵90°角的补角的度数是90°，
∴说一个角的补角一定大于这个角错误，故（2）错误；
（3）若两个角是同一个角的补角，则它们相等；故（3）正确；
（4）锐角和钝角不一定互补，
∵如∠A=10°，∠B=100°，当两角不互补，
∴说锐角和钝角互补错误，故（3）错误；
故答案为：（1）（3）．
【点睛】本题考查了补角和余角的定义，以及补角的性质：同角的补角相等，理解定义是关键．
15. 已知∠α和∠β互为补角，并且∠β的一半比∠α小30°，则∠α＝_____，∠β＝_____．
【答案】 ①. 80°##80度 ②. 100°##100度
【解析】
【分析】根据互为补角的和等于180°，得到α=180°-β，然后根据题意列出关于β的一元一次方程，求解即可．
【详解】解：∵∠α和∠β互为补角，
∴α=180°-β，
根据题意得，180°-β-β=30°，
解得β=100°，
α=180°-β=80°，
故答案为：80°，100°．
【点睛】本题考查了互为补角的和等于180°的性质，根据题意列出一元一次方程是解题的关键．
16. 已知|x|＝2，|y|＝1，且|x﹣y|＝y﹣x，则x-y=____．
【答案】-3或-1##-1或-3
【解析】
【分析】根据绝对值的意义得到x=-2，y=1或y=1，然后计算x-y的值．
【详解】解：∵|x-y|=y-x，
∴y>x，
∵|x|=2，|y|=1，
∴x=-2，y=1或y=1，
当x=-2，y=1时，x-y=-2-1=-3；
当x=-2，y=-1时，x-y=-2+1=-1．
故答案为：-3或-1．
【点睛】本题考查了有理数的减法以及绝对值，根据题意得出x、y的值是解得本题的关键．
三、解答题（本大题共9小题，满分72分．解答应写出文字说明、证明过程或演算步骤．）
17. 计算：4+（﹣2）3×5﹣（﹣0.28）÷4．
【答案】
【解析】
【详解】解：

．
【点睛】本题主要考查了有理数的混合运算，熟练掌握有理数的混合运算法则是解题的关键．
18. 解方程：
【答案】
【解析】
【分析】根据解方程的一般步骤：去分母、去括号、移项合并同类项、系数化为1进行计算即可．
【详解】去分母，得，
去括号，得，
移项，得，
合并同类项，得，
系数化为1，得.
【点睛】本题考查解一元一次方程的知识，解方程的一般步骤：去分母、去括号、移项合并同类项、系数化为1；熟练掌握解一元一次方程的步骤是解题关键.
19. 如图，已知线段a，b，其中AB=a．
（1）用尺规作图法，在AB延长线上，作一点C，使得BC=b．（不写作法，保留作图痕迹）；
（2）在（1）的条件下，若a=2，b=1，AC的中点为M，求线段AM的长．
【答案】（1）作图见解析
（2）AM的长为
【解析】
【分析】（1）如图，以为圆心，以b为半径画弧与延长线的交点为C，BC即为所求；
（2）由题意知，，计算求解即可．
【小问1详解】
解：如图，以为圆心，以b为半径画弧与延长线的交点为C，BC即为所求；
【小问2详解】
解：∵
∴
∵AC的中点为M
∴
∴的长为．
【点睛】本题考查了画线段，线段的中点，线段的和差．解题的关键在于明确线段之间的数量关系．
20. 先化简，在求值：，其中，．
【答案】；
【解析】
【分析】通过去括号，合并同类项，化简代数式，后代入计算．
【详解】解：原式
当，，
原式．
【点睛】本题考查了整式加减中化简求值，熟练去括号，正确合并同类项是解题的关键．
21. 一套仪器由一个A部件和三个B部件构成，用1立方米钢材可做40个A部件或240个B部件．现要用6立方米钢材制作这种仪器，应用多少钢材制作A部件，才能使生产的A、B刚好配套？恰好配成这种仪器多少套？
【答案】应用4做A部件，才能使生产的A、B刚好配套恰好配成这种仪器160套
【解析】
【分析】设x立方用来做A部件，（6－x）立方用来做B部件．根据题意列出一元一次方程，进而求得恰好配成多少套．
【详解】解：设x立方用来做A部件，（6－x）立方用来做B部件．
解得
∴
∴4做A部件，2做B部件．
A：
∴共能做160套仪器．
答：应用4做A部件，才能使生产的A、B刚好配套恰好配成这种仪器160套
【点睛】本题考查了一元一次方程的应用，根据题意列出方程是解题的关键．
22. 如图，OB为∠AOC的平分线，OD是∠COE的平分线．
（1）如果∠AOB＝40°，∠DOE＝30°，那么∠BOD为多少度？
（2）如果∠AOE＝140°，∠COD＝30°，那么∠AOB为多少度？
【答案】（1）70°；（2）40°
【解析】
【分析】（1）根据角平分线的定义可以求得∠BOD=∠AOB+∠DOE；
（2）根据角平分线的定义易求得∠EOC=2∠COD=60°，所以由图中的角与角间的和差关系可以求得∠AOC=80°，最后由角平分线的定义求解．
【详解】解：（1）因为OB为∠AOC的平分线，OD是∠COE的平分线，
所以∠AOB＝∠BOC，∠DOE＝∠DOC．
所以∠BOD＝∠BOC＋∠DOC＝∠AOB＋∠DOE＝40°＋30°＝70°；
（2）因为OD是∠COE的平分线，∠COD＝30°，
所以∠EOC＝2∠COD＝60°．
因为∠AOE＝140°，∠AOC＝∠AOE－∠EOC＝80°．
又因为OB为∠AOC的平分线，
所以∠AOB＝∠AOC＝40°．
【点睛】本题考查了角平分线的定义．从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线，注意使用几何符号语言描述．
23. 某商店有两种书包，每个小书包比大书包的进价少10元，而它们的售后利润额相同．其中，每个小书包的盈利率为，每个大书包的盈利率为，试求两种书包的进价．
【答案】小书包20元，大书包30元
【解析】
【分析】设每个小书包的进价为x元，则每个大书包的进价为（x+10）元，根据利润＝进价×盈利率结合两种书包的售后利润额相同，即可得出关于x的一元一次方程，解之即可得出结论．
【详解】设每个小书包的进价为x元，则每个大书包的进价为（x+10）元，
依题意得：30%x＝20%（x+10），
解得：x＝20，
则x+10＝30．
答：每个小书包的进价为20元，每个大书包的进价为30元．
【点睛】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
24. （1）已知|x﹣3|+（y+1）2＝0，代数式的值比y﹣x+t多1，求t的值．
（2）m为何值时，关于x的一元一次方程4x﹣2m＝3x﹣1的解是x＝2x﹣3m的解的2倍．
【答案】（1）t=1；（2）m=-．
【解析】
【分析】（1）先根据|x-3|+（y+1）2=0，求出x，y的值，再根据代数式的值比y-x+t多1列出方程，把x，y的值代入解出x的值；
（2）分别表示出两方程的解，根据解的关系确定出m的值即可．
【详解】解：（1）∵|x-3|+（y+1）2=0，而|x-3|≥0，（y+1）2≥0，
∴x-3=0，y+1=0，
∴x=3，y=-1，
∵代数式的值比y-x+t多1，
∴-( y-x+t) =1，
即+1+3-t=1，
解得：t=1；
（2）方程4x-2m=3x-1，
解得：x=2m-1，
方程x=2x-3m，
解得：x=3m，
由题意得：2m-1=6m，
解得：m=-．
【点睛】本题考查了解一元一次方程，以及非负数的性质，熟练掌握运算法则是解本题的关键．
25. 数轴上两点A、B，A在B左边，原点O是线段AB上的一点，已知AB=4，且OB=3OA．A、B对应的数分别是a、b，点P为数轴上的一动点，其对应的数为x．
（1）a= ，b= ，并在数轴上面标出A、B两点；
（2）若PA=2PB，求x的值；
（3）若点P以每秒2个单位长度的速度从原点O向右运动，同时点A以每秒1个单位长度的速度向左运动，点B以每秒3个单位长度的速度向右运动，设运动时间为t秒．请问在运动过程中，3PB-PA的值是否随着时间t的变化而改变？若变化，请说明理由若不变，请求其值．
【答案】（1），作图见解析
（2）或
（3）不变，8，理由见解析
【解析】
【分析】（1）根据AB=4，且OB=3OA，即可确定a、b的值．
（2）分别用含x的解析式表示出PA和PB的长度，再根据PA=2PB建立等式，就可以求出x的值．
（3）分别表示出t秒后A、B、P的值，再代入3PB-PA，并化简就可以确定这是一个定值．
【小问1详解】
解： AB=4，且OB=3OA，A、B对应的数分别是a、b，
故答案为：
【小问2详解】
解：①当P点在A点左侧时，PA②当P点位于A、B两点之间
解得
③当P点在B点右侧时
解得
故x的值为解得或．
【小问3详解】
解：t秒后，A点的值为，P点的值为2t，B点的值为
所以3PB-PA的值为定值，不随着时间t的变化而改变．
【点睛】此题考查了数轴两点之间距离、动点的坐标值的表示以及代数式定值问题的证明，解题的关键是动点坐标值的表示以及分类讨论思想的运用